2 장 로지스틱 회귀모형
선형회귀모형에서는 반응변수가 연속형 변수임을 가정하고 있다. 그러나 범주형 변수를 반응변수로 하여 회귀모형을 설정해야 하는 경우도 많이 있는데, 이런 상황에서 선형회귀모형을 그대로 사용해도 괜찮은지 여부를 확인할 필요가 있으며, 만일 문제가 있다면 대안으로 사용할 수 있는 모형이 무엇인지 알아보아야 한다.
범주형 변수가 “성공”, “실패”와 같이 2개의 범주만을 갖는 경우에는 이항변수, 범주의 개수가 3개 이상인 경우에는 다항변수라고 부른다. 이 장에서는 이항변수를 반응변수로 설정해야 하는 경우에 적용할 수 있는 로지스틱 회귀모형에 대하여 살펴보겠다.
2.1 이항반응변수에 대한 선형회귀모형의 한계
반응변수 \(Y\) 와 설명변수 \(X_{1}, \ldots, X_{k}\) 로 구성된 선형회귀모형은 다음과 같이 표현된다.
\[\begin{equation} Y = \beta_{0} + \beta_{1} + \cdots + \beta_{k}X_{k} + \varepsilon \tag{2.1} \end{equation}\] 단, \(\varepsilon \sim N(0, \sigma^{2})\).
반응변수의 조건부 기대값은 다음과 같다.
\[\begin{equation} E(Y|X)=\beta_{0}+\beta_{1}X_{1}+\cdots+\beta_{k}X_{k} \tag{2.2} \end{equation}\]
이항반응변수 \(Y\) 는 “성공” 범주에 속하면 1, “실패” 범주에 속하면 0을 값으로 갖는 것이 일반적으로 적용되는 방식이다. 두 개의 값만을 가질 수 있는 이항반응변수를 모형 (2.1)으로 설명할 때 발생할 수 있는 첫 번째 문제는 오차항 \(\varepsilon\) 이 \(N(0,\sigma^{2})\) 의 분포를 한다는 가정을 만족시킬 수 없다는 것이다.
두 번째 문제는 반응변수의 조건부 기대값 \(E(Y|X)\) 와 설명변수의 선형결합인 \(\beta_{0}+\beta_{1}X_{1}+\cdots+\beta_{k}X_{k}\) 의 범위가 일치하지 않는다는 것이다. 이항반응변수 \(Y\) 는 베르누이 분포를 따른다고 할 수 있는데, 이 경우 조건부 기대값은 다음과 같이 계산된다.
\[\begin{align*} E(Y|X) &= 1 \cdot P(Y=1|X) + 0 \cdot P(Y=0|X) \\ &= P(Y=1|X) \end{align*}\]
즉, 이항반응변수의 조건부 기대값은 반응변수가 1이 될 확률이 되며, 따라서 범위는 \((0,1)\) 이 된다. 반면에 설명변수가 취할 수 있는 값에 특별한 제약조건이 없다면 설명변수의 선형결합 \(\beta_{0}+\beta_{1}X_{1}+\cdots+\beta_{k}X_{k}\) 의 범위는 \((-\infty, \infty)\) 가 되기 때문에, \(E(Y|X)\) 와 설명변수의 선형결합이 취하는 값의 범위는 일치하지 않게 된다.
선형회귀모형을 사용하여 이항반응변수가 “성공” 범주에 속할 확률을 추정하게 되면, 어떠한 문제가 발생할 수 있는지 예제를 통해서 살펴보도록 하자.
\(\bullet\) 예제 : ISLR::Default
패키지 ISLR의 데이터 프레임 Default는 신용카드 사용 금액을 매달 갚아가는 상황에 대한 모의자료이다.
변수 default는 연체 여부를 나타내는 요인으로 "No"와 "Yes"의 두 범주를 갖고 있는 이항반응변수이다.
student는 학생 여부에 대한 요인이고, balance는 카드 사용 금액 중 갚고 남은 잔액, income은 소득을 나타낸다.
data(Default, package = "ISLR")
str(Default)
## 'data.frame': 10000 obs. of 4 variables:
## $ default: Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 ...
## $ student: Factor w/ 2 levels "No","Yes": 1 2 1 1 1 2 1 2 1 1 ...
## $ balance: num 730 817 1074 529 786 ...
## $ income : num 44362 12106 31767 35704 38463 ...변수 default의 값을 "No"는 0으로, "Yes"는 1로 바꾸고,
default를 반응변수, balance를 설명변수로 하는 선형회귀모형을 적합하여 그 결과를 두 변수의 산점도에 함께 표시해 보자.
요인 default를 함수 as.numeric()을 사용하여 숫자형으로 변환시키면 첫 번째 범주인 "No"가 1로, 두 번째 범주인 "Yes"가 2로 변하게 된다. 여기에 1을 더 빼서 "No"를 0으로, "Yes"를 1로 변환하였다.
library(tidyverse)
Default |>
ggplot(aes(x = balance, y = as.numeric(default)-1)) +
geom_jitter(height = 0.005, width = 100) +
geom_smooth(method = "lm", se = FALSE) +
labs(y = "Probability of Default")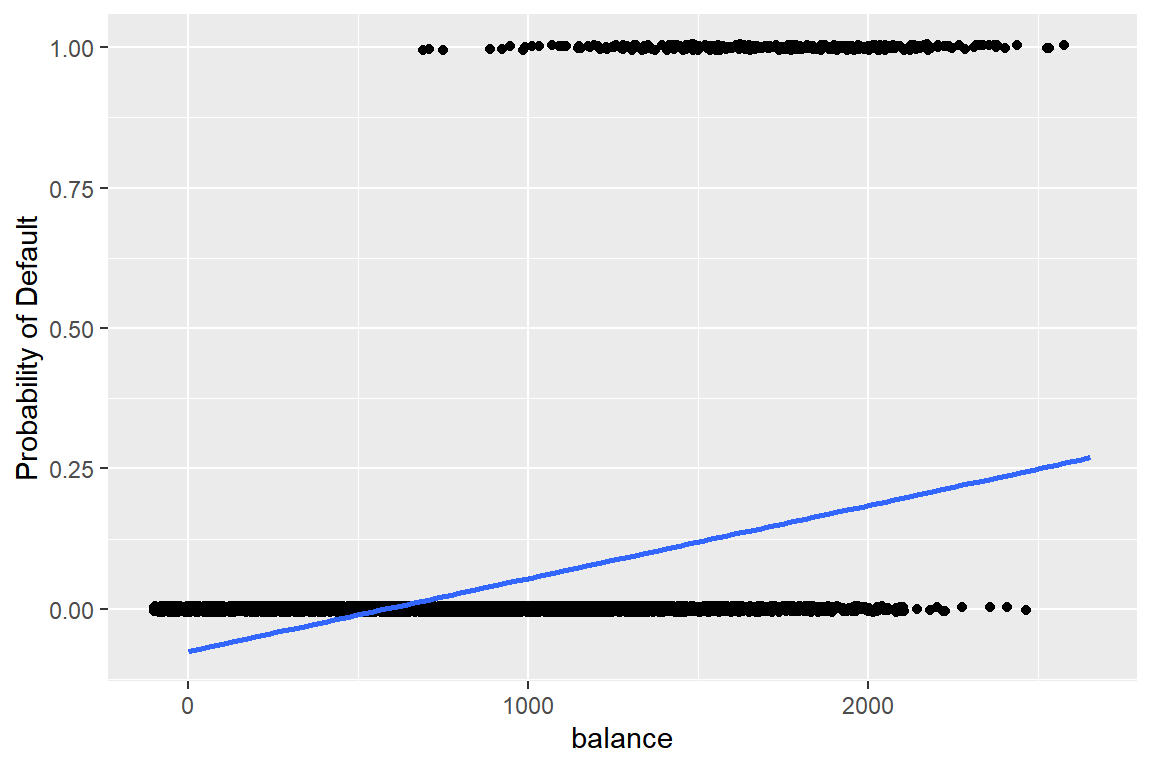
그림 2.1: 이항반응변수를 선형회귀모형으로 적합한 결과
그림 2.1에 표시된 파란색 회귀직선은 주어진 balance의 값에서 default가 1이 될 확률을 선형회귀모형으로 추정한 결과이다.
balance가 매우 작은 값을 갖는 영역에서 default가 1이 될 확률이 음으로 추정된 것을 볼 수 있다.
또한 회귀직선이 점들을 거의 설명하지 못하고 있음도 확인할 수 있다.
이항반응변수에 대해서는 적절하지 않은 모형으로 보인다.
그림 2.2는 로지스틱 회귀모형으로 default가 1이 될 확률을 추정한 결과이다.
선형회귀모형이 갖고 있던 두 가지 문제가 모두 해결된 것을 볼 수 있다.
Default |>
ggplot(aes(x = balance, y = as.numeric(default)-1)) +
geom_jitter(height = 0.005, width = 100) +
geom_smooth(method = "glm", method.args = list(family = binomial),
se = FALSE) +
labs(y = "Probability of Default")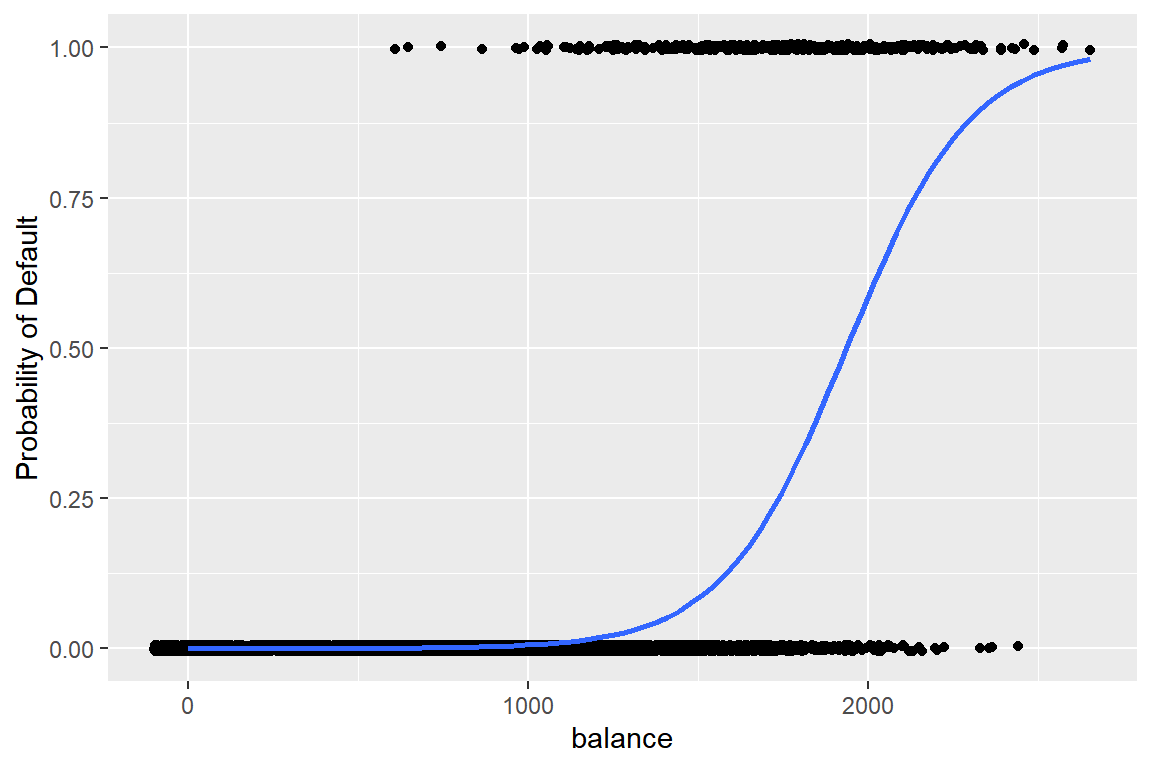
그림 2.2: 이항반응변수를 로지스틱 회귀모형에 적합한 결과
함수 geom_smooth()에서 사용된 method = "glm"과 family = binomial에 대한 설명은 로지스틱 회귀모형의 적합에 사용되는 함수 glm()에 대한 소개에서 진행하겠다.
2.2 로지스틱 회귀모형
선형회귀모형을 사용하여 변수 default가 1이 될 확률을 추정한 결과에서 음의 값이 나온 이유는 2.1절에서 살펴본 데로 설명변수가 취할 수 있는 값의 범위가 반응변수의 기댓값이 취할 수 있는 값의 범위와 다르기 때문이다.
즉, 선형회귀모형에서는 \(E(Y|X) = P(Y=1|X) = \beta_{0} + \beta_{1}X\) 로 설정되는데,
\(0 \leq P(Y=1|X) \leq 1\) 이고, \(-\infty < \beta_{0}+\beta_{1}X < \infty\) 이기 때문에 서로 범위가 맞지 않는다.
이 문제는 \(P(Y=1|X)\) 에 적절한 변환을 실시함으로써 해결을 할 수 있다. 먼저 반응변수 \(Y\) 가 1이 될 사건에 대한 odds를 생각해 보자. Odds의 범위는 0에서 무한대가 된다.
\[\begin{equation} 0 \leq \frac{P(Y=1|X)}{1-P(Y=1|X)} < \infty \end{equation}\]
이어서 \(Y\) 가 1이 될 사건에 대한 log odds 또는 logit 변환을 생각해 보자. 설명변수의 선형결합과의 범위 불일치 문제가 해결되었음을 알 수 있다.
\[\begin{equation} -\infty < \log \left(\frac{P(Y=1|X)}{1-P(Y=1|X)}\right) < \infty \end{equation}\]
\(Y\) 가 1이 될 사건에 대한 logit 변환을 적용한 로지스틱 회귀모형은 다음과 같이 정의된다.
\[\begin{equation} \log \left(\frac{P(Y=1|X)}{1-P(Y=1|X)}\right) = \beta_{0} + \beta_{1}X_{1} + \cdots + \beta_{k}X_{k} \tag{2.3} \end{equation}\]
반응변수가 1이 될 확률은 모형 (2.3)의 inverse logit 변환으로 다음과 같이 표현된다.
\[\begin{equation} P(Y=1|X) = \frac{e^{\beta_{0} + \beta_{1}X_{1} + \cdots + \beta_{k}X_{k}}}{1+e^{\beta_{0} + \beta_{1}X_{1} + \cdots + \beta_{k}X_{k}}} \end{equation}\]
\(\bullet\) 로지스틱 회귀식의 특징
설명변수가 한 개인 로지스틱 회귀모형을 대상으로 절편과 기울기를 나타내는 회귀계수의 역할을 살펴보자. 예를 들어, 반응변수가 1이 될 확률이 \(P(Y=1|X)=e^{b0+b1X}/(1+e^{b0+b1X})\) 로 표현된다고 하자. 그림 2.3의 첫 번째 그래프는 \(b1=1\) 로 고정하고, \(b0\) 의 값을 \(-4, ~0, ~4\) 로 변화시켰을때 \(P(Y=1|X)\) 의 값을 나타낸 것이고, 두 번째 그래프는 \(b0 = 0\) 으로 고정하고, \(b1\)의 값을 \(0.25, ~ 0.5, ~1\) 로 변화시켰을때 \(P(Y=1|X)\) 의 값을 나타낸 것이다.
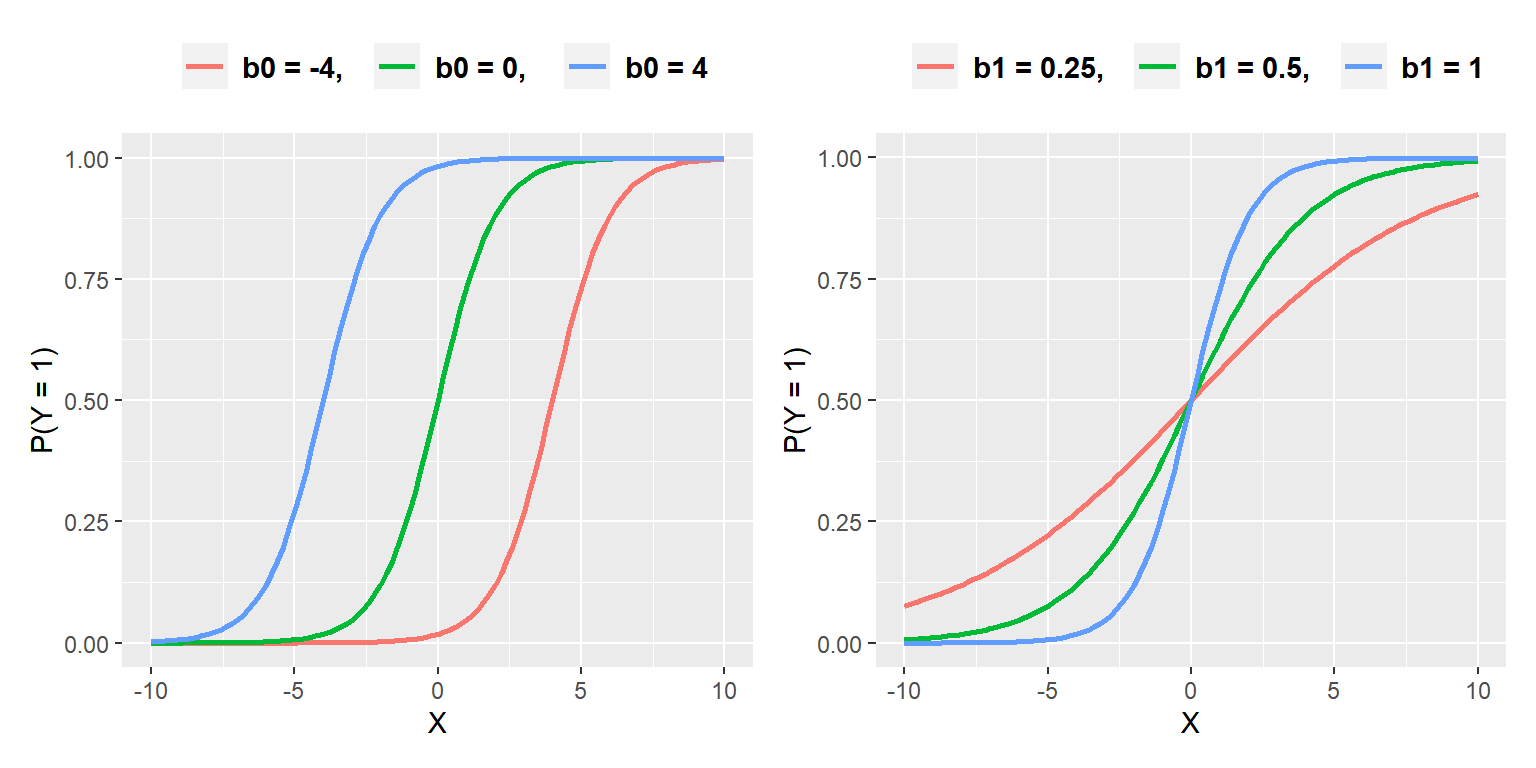
그림 2.3: 로지스틱 회귀계수의 역할
로지스틱 회귀곡선은 절편이 증가함에 따라 왼쪽으로 이동되는 것을 알 수 있는데, 이것은 고정된 설명변수의 수준에서 절편이 증가함에 따라 반응변수가 1이 될 확률이 증가하는 것을 보여준다. 또한 기울기가 증가함에 따라 반응변수가 1이 될 확률이 급격하게 증가하는 것을 볼 수 있다.
2.2.1 모형 적합
회귀모형의 적합이란 모형 (2.3)에 포함된 회귀계수 \(\beta_{0}, \beta_{1}, \ldots, \beta_{k}\) 의 추정을 의미한다. 반응변수 \(Y\) 가 0 또는 1을 값으로 갖는 베르누이 분포를 하고 있기 때문에 회귀계수는 maximum likelihood estimation으로 추정을 할 수 있는데, 다만 우도함수의 형태가 방정식을 유도하여 회귀계수의 값을 구할 수 있는 형태가 아니기 때문에 수치적인 반복 계산으로 추정하게 된다.
설정된 모형에 큰 문제가 없다면 대부분의 경우 몇 번의 반복으로 모수를 추정할 수 있다. 그러나 여러 번의 반복 계산을 수행하여도 수렴 기준을 충족하지 못해 결국 추정에 실패하는 경우도 있는데, 그 이유 중에 하나가 complete separation이다. Complete separation은 특정 설명변수의 선형결합으로 반응변수의 값이 완벽하게 분리되는 상태를 의미하는 것인데, 예를 들어 설명변수 \(X\) 가 10 미만의 값을 가지면 반응변수 \(Y\) 는 항상 0이 되고, \(X\) 가 10 이상의 값을 가지면 \(Y\) 는 항상 1이 된다면, 설명변수 \(X\) 로 반응변수의 두 그룹이 완벽하게 분리되는 것이다. Complete separation이 발생할 수 있는 몇 가지 상황이 있는데, 먼저 범주형 설명변수의 특정 범주에 대해 반응변수가 모두 0 또는 1의 값을 갖는 경우이다. 예를 들어, 반응변수가 나이와 밀접하게 연관된 질환의 유무이고 설명변수에 나이를 그룹으로 구분한 범주형 변수가 포함되면, 특정 나이 그룹에서는 모두 질환이 있는 것으로 나타나지만, 질환이 전혀 없는 나이 그룹이 나타날 수 있는 것이다. 또한 희귀 사건을 반응변수로 다루고 있는 경우와 표본의 크기가 작은 경우에도 complete separation이 발생할 수 있다.
로지스틱 회귀모형의 적합은 일반화선형모형(generalize linear model) 적합을 위한 함수 glm()으로 할 수 있다.
기본적인 사용법은 glm(formula, family = binomial, data)이다.
formula에는 ‘반응변수 ~ 설명변수’ 형식의 공식이 지정되는데, 반응변수의 유형은 0 또는 1을 값으로 갖는 숫자형 벡터이거나 요인이어야 한다.
요인인 경우에는 첫 번째 범주가 ‘실패’, 두 번째 범주가 ‘성공’으로 분류되어 ‘성공’ 확률을 추정하게 된다.
family는 일반화선형모형에서 반응변수의 분포 및 link function을 지정하는 것으로서 로지스틱 회귀모형의 경우에는 binomial을 지정해야 한다.
\(\bullet\) 예제: ISLR::Default
2.1절에서 살펴본 Default 자료에서 default를 반응변수, balance와 student, 그리고 income을 설명변수로 하며, default가 두 번째 범주인 "Yes"과 되 홧률에 대한 로지스틱 회귀모형을 적합해 보자.
단, income은 $1,000 단위로 조절한다.
먼저 산점도행렬을 작성해서 변수들 사이의 관계를 살펴보자.
변수 default가 "Yes"인 경우가 매우 드물다는 것을 알 수 있다.
또한 default가 "Yes"와 "No"인 그룹에서 balance의 분포는 큰 차이를 보이는 반면에 income은 거의 비슷한 분포를 갖고 있다.
Default <- Default |>
mutate(income = income/1000)
GGally::ggpairs(Default, aes(fill = default), showStrips = TRUE)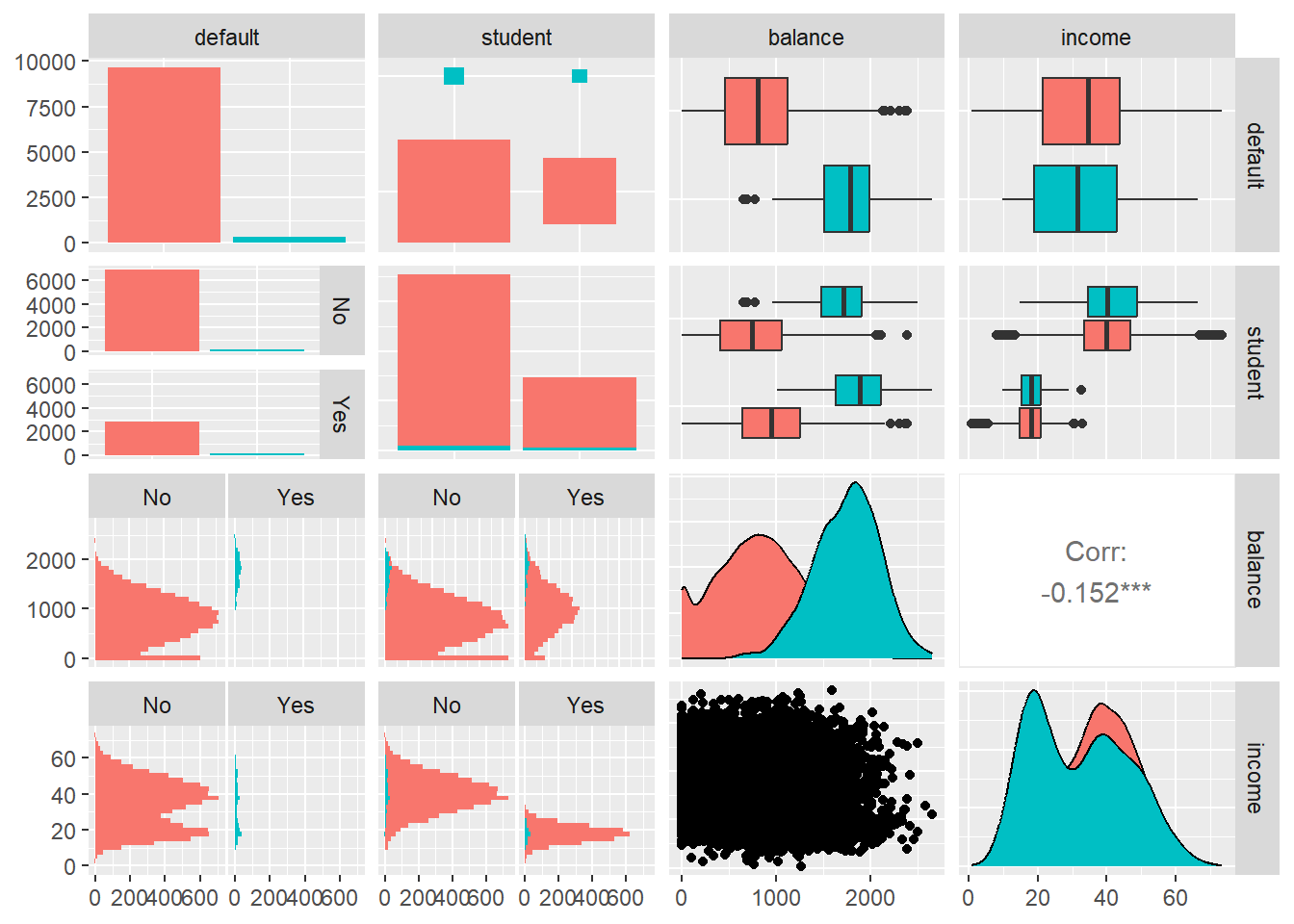
그림 2.4: Default 자료의 산점도행렬
이제 로지스틱 회귀모형을 적합해 보자. 모형의 주요한 적합 결과는 함수 summary()로 확인할 수 있다.
fit <- glm(default ~ ., family = binomial, Default)
summary(fit)
##
## Call:
## glm(formula = default ~ ., family = binomial, data = Default)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.087e+01 4.923e-01 -22.080 < 2e-16 ***
## studentYes -6.468e-01 2.363e-01 -2.738 0.00619 **
## balance 5.737e-03 2.319e-04 24.738 < 2e-16 ***
## income 3.034e-03 8.203e-03 0.370 0.71152
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 2920.6 on 9999 degrees of freedom
## Residual deviance: 1571.5 on 9996 degrees of freedom
## AIC: 1579.5
##
## Number of Fisher Scoring iterations: 8개별 회귀계수에 대한 유의성 검정 결과를 볼 수 있다.
가변수가 사용된 요인 student에 대해서는 "No" 그룹과 "Yes" 그룹 사이에 유의적인 차이가 있는 것으로 나타났고, balance도 유의적인 변수로 나타났다.
마지막 부분에 deviance가 계산되어 있는데, deviance는 일반화선형모형의 적합도를 측정할 때 사용되는 통계량으로서 추정된 모형의 적합값과 실제 관찰값의 일치 정도를 측정한다고 할 수 있다. Null deviance는 절편만 있는 모형과 주어진 자료를 완전하게 설명하는 완전모형(saturated model)과의 적합도 차이이고, residual deviance는 현재의 모형과 완전모형의 적합도 차이이다. 따라서 두 deviance의 차이는 현재 모형에 포함된 설명변수가 모형의 적합도 향상에 어느 정도 기여했는지를 측정할 수 있는 도구가 된다. 즉, 만일 현재 모형에 \(k\) 개의 설명변수가 포함되어 있다면, 현재 모형의 유의성 검정인 \(H_{0}:\beta_{1} = \cdots = \beta_{k} = 0\) 에 대한 검정통계량으로 사용될 수 있다는 것이다. 두 deviance의 차이는 귀무가설이 사실일 때 \(\chi^{2}\)분포를 하고, 자유도는 두 모형을 구성하는 모수 개수의 차이이다.
현재 모형의 유의성 검정은 함수 anova()를 사용하여 다음의 방식으로도 실시할 수 있다.
귀무가설은 기각되며, 따라서 3개의 설명변수 중 적어도 하나는 유의한 변수라는 의미가 된다.
fit_null <- glm(default ~ 1, family = binomial, Default)
fit <- glm(default ~ ., family = binomial, Default)anova(fit_null, fit, test = "Chisq")
## Analysis of Deviance Table
##
## Model 1: default ~ 1
## Model 2: default ~ student + balance + income
## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1 9999 2920.7
## 2 9996 1571.5 3 1349.1 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1\(\bullet\) 설명변수의 효과 분석
개별 설명변수의 효과 분석은 로지스틱 회귀모형에서도 중요한 의미를 가지고 있으나, 선형회귀모형의 경우와는 조금 다른 방식으로 이루어져야 한다. 선형회귀모형은 다른 변수가 고정된 상태에서 \(X_{j}\) 를 한 단위 변화시키면 \(E(Y|X)\) 가 \(\beta_{j}\) 만큼 변동되는 구조를 가지고 있다. 반면에 로지스틱 회귀모형은 개별 설명변수의 효과를 odds ratio로 나타내야 하는 구조를 가지고 있다. 즉, 로지스틱 회귀모형은 log odds에 대한 모형이다.
\[\begin{align*} \log \left(\frac{P(Y=1|X)}{1-P(Y=1|X)}\right) &= \log \Omega (X) \\ &= \beta_{0} + \beta_{1}X_{1} + \cdots + \beta_{k}X_{k} \end{align*}\]
이것을 odds에 대한 모형으로 변환시켜 보자.
\[\begin{align*} \Omega(X) &= e^{\beta_{0} + \beta_{1}X_{1} + \cdots + \beta_{k}X_{k}} \\ &= e^{\beta_{0}} e^{\beta_{1}X_{1}} \cdots e^{\beta_{k}X_{k}} \end{align*}\]
다른 변수는 모두 고정시키고 \(X_{j}\) 만 \(\delta\) 만큼 변화시킬 때의 odds는 다음과 같이 표현된다.
\[\begin{equation} \Omega(X; X_{j}+\delta) = e^{\beta_{0}} e^{\beta_{1}X_{1}} \cdots e^{\beta_{j}(X_{j}+\delta)} \cdots e^{\beta_{k}X_{k}} \end{equation}\]
다른 변수는 모두 고정시키고 \(X_{j}\) 만 \(\delta\) 만큼 변화시킬 때의 odds의 변화 정도는 \(\Omega(X)\) 와 \(\Omega(X; X_{j}+\delta)\) 의 비율인 odds ratio로 나타낼 수 있다.
\[\begin{equation} \frac{\Omega(X; X_{j}+\delta)}{\Omega(X)} = e^{\beta_{j}\delta} \end{equation}\]
Odds ratio가 1보다 작은 값을 갖는 경우에는 해당 설명변수의 값을 증가시키면 반응변수가 ‘성공’ 범주가 될 odds가 감소하는 것이고, 1보다 큰 값을 갖는 경우에는 ‘성공’ 범주가 될 odds가 증가하는 것이 된다.
Default 자료에서 적합된 로지스틱 회귀모형 fit에 포함된 각 설명변수의 odds ratio를 구해보자.
fit을 함수 coef()에 입력해서 회귀계수를 추출하고,
이어서 exp()로 변환시키면 odds ratio가 계산된다.
coef(fit) |> exp() |> round(6)
## (Intercept) studentYes balance income
## 0.000019 0.523732 1.005753 1.003038변수 balance의 값이 $1 증가하면 default가 "Yes"가 될 odds가 0.57% 증가하는 것으로 추정되며,
student의 경우에는 "Yes" 그룹이 "No" 그룹에 비해 default가 "Yes"가 될 odds를 (1-0.5237)*100%,
즉 47.63% 감소시키는 것으로 나타났다.
Odds ratio에 대한 신뢰구간은 fit을 함수 confint()에 입력해서 회귀계수의 신뢰구간을 계산하고,
이어서 exp()로 변환시키면 odds ratio에 대한 신뢰구간이 계산된다.
함수 confint()의 디폴트 level은 0.95이다.
confint(fit) |> exp() |> round(6)
## 2.5 % 97.5 %
## (Intercept) 0.000007 0.000049
## studentYes 0.329883 0.833422
## balance 1.005309 1.006224
## income 0.987038 1.019309odds ratio(\(e^{\beta_{j}}\))의 신뢰구간에 1이 포함된다는 것은 회귀계수(\(\beta_{j}\))의 신뢰구간에 0이 포함되는 것과 동일한 것이다. 따라서 변수 income은 5% 유의수준에서 비유의적이다.
2.2.2 확률 예측
로지스틱 회귀모형은 반응변수가 ‘성공’ 범주에 속할 확률을 추정하기 위한 회귀모형이다. 회귀계수가 추정되면 \(\pi(\mathbf{x}) = P(Y=1|\mathbf{x})\) 을 다음과 같이 추정할 수 있다.
\[\begin{equation} \hat{\pi}(\mathbf{x}) = \frac{e^{\hat{\beta}_{0} + \cdots + \hat{\beta}_{k}x_{k}}}{1+e^{\hat{\beta}_{0} + \cdots + \hat{\beta}_{k}x_{k}}} \end{equation}\]
확률 예측은 함수 predict()로 할 수 있으며, 기본적인 사용법은 predict(object, newdata, type = "response")이다.
object에는 적합한 로지스틱 모형에 대한 glm 객체를 지정하고,
newdata에는 예측에 사용될 설명변수의 새로운 자료를 데이터 프레임의 형태로 지정한다.
type은 예측의 유형을 지정하는 것으로서 반응변수가 ‘성공’ 범주에 속할 확률을 예측하고자 하는 경우에는 반드시 "response"를 지정해야 한다.
\(\bullet\) 예제: ISLR::Default
2.2.1절의 예제에서 적합한 모형 fit을 대상으로 balance의 값이 $1,500이고, income이 $40,000, 그리고 student가 "Yes"와 "No"인 경우에 대하여 각각 default가 "Yes"일 확률을 추정해 보자.
우선 예측에 사용될 설명변수의 새로운 데이터 프레임 new_df를 다음과 같이 설정한다.
이제 모형 fit을 대상으로 new_df에 대한 예측을 실시해 보자.
이번에는 모형 추정에 사용된 기존의 자료를 대상으로 default가 Yes가 될 확률을 추정해서 그래프로 나타내 보자.
함수 predict()에서 newdata를 생략하면 기존 자료에 대한 확률이 예측된다.
Default |>
mutate(pred = predict(fit, type = "response")) |>
ggplot(aes(x = balance, y = as.numeric(default)-1)) +
geom_jitter(height = 0.005, width = 100) +
geom_line(aes(x = balance, y = pred, color = student), linewidth = 1) +
labs(y = "Probability of default")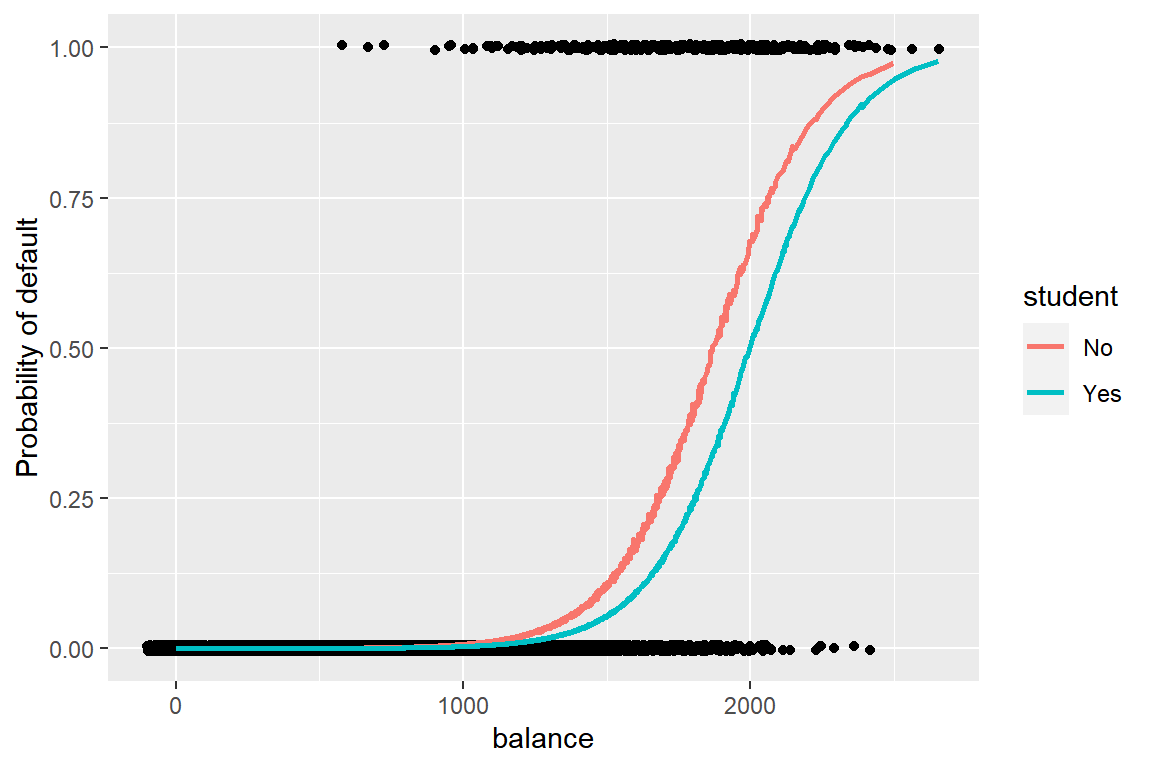
그림 2.5: student와 balance에 따른 default 확률
변수 balance의 값이 증가하면 default가 "Yes"가 될 확률이 증가하고 있다.
또한 주어진 balance 값에 대하여 student가 "Yes"인 그룹이 "No"인 그룹에 비하여 default가 "Yes"가 될 확률이 낮음을 알 수 있다.
2.3 변수선택
선형회귀모형의 경우와 마찬가지로 로지스틱 회귀모형에서도 ‘최적’ 변수로 이루어진 모형을 찾는 것은 매우 중요한 작업이다. 1.3절에서 살펴본 선형회귀모형의 평가측도에 의한 best subset selection과 stepwise selection, 그리고 lasso 모형의 적용 과정 등이 로지스틱 회귀모형에도 큰 차이 없이 적용된다. 다만 모형의 차이로 인하여 사용할 수 있는 평가 측도에 차이가 있는데, AIC, BIC와 2.5절에서 살펴볼 accuracy, F1 score, AUC 등의 분류성능 평가에 관련된 측도가 로지스틱 회귀모형에 적용할 수 있는 평가 측도가 된다.
변수선택에 사용될 함수는 stepwise selection과 lasso 모형의 경우에는 선형회귀모형의 경우와 동일하지만,
best subset selection의 경우에는 bestglm::bestglm()를 사용해야 한다.
기본적인 사용법은 bestglm(Xy, family = binomial, IC = c("BIC", "AIC"))이다.
Xy는 반응변수와 설명변수로 구성된 데이터 프레임인데, 반응변수가 마지막 열에 위치해야 한다.
IC는 변수선택 기준으로 사용되는 통계량으로서 "BIC"가 디폴트로 사용된다.
\(\bullet\) 예제 carData::Mroz
Mroz는 미국 753명 여성을 대상으로 직업 참여율과 관련된 8개 항목을 조사한 자료이다.
data(Mroz, package = "carData")
str(Mroz)
## 'data.frame': 753 obs. of 8 variables:
## $ lfp : Factor w/ 2 levels "no","yes": 2 2 2 2 2 2 2 2 2 2 ...
## $ k5 : int 1 0 1 0 1 0 0 0 0 0 ...
## $ k618: int 0 2 3 3 2 0 2 0 2 2 ...
## $ age : int 32 30 35 34 31 54 37 54 48 39 ...
## $ wc : Factor w/ 2 levels "no","yes": 1 1 1 1 2 1 2 1 1 1 ...
## $ hc : Factor w/ 2 levels "no","yes": 1 1 1 1 1 1 1 1 1 1 ...
## $ lwg : num 1.2102 0.3285 1.5141 0.0921 1.5243 ...
## $ inc : num 10.9 19.5 12 6.8 20.1 ...반응변수 lfp는 직업 유무를 나타내는 요인이고, 설명변수 k5는 5세 이하 자녀의 수,
k618은 6세에서 18세 사이 자녀의 수, age는 여성의 나이, wc는 여성의 대학과정 등록 여부,
hc는 남편의 대학과정 등록 여부, lwg는 여성의 기대 수입의 로그값, inc는 여성을 제외한 가구원의 총소득이다.
- Best subset selection
함수 bestglm::bestglm()을 사용하여 설명변수의 모든 가능한 조합에 대하여 AIC 또는 BIC를 기준으로 모형을 선택해 보자.
Mroz에 적용하기 위해서 먼저 반응변수 lfp를 마지막 열로 이동한 데이터 프레임 Xy를 다음과 같이 생성하자.
이제 AIC와 BIC를 기준으로 각각 변수선택을 실시해 보자.
library(bestglm)
fit_bic <- bestglm(Xy, family = binomial)
fit_aic <- bestglm(Xy, family = binomial, IC = "AIC")BIC에 의한 선택 결과를 확인해 보자.
fit_bic의 요소 Subsets에는 설명변수의 개수가 \(i=0, \ldots, k\) 인 모형 중 최적 모형의 적합결과가 입력되어 있으며, 그 중 BIC가 가장 작은 ‘최적’ 모형은 변수 개수에 별표가 추가되어 있다.
fit_bic$Subsets
## Intercept k5 k618 age wc hc lwg inc logLikelihood BIC
## 0 TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE -514.8732 1029.7464
## 1 TRUE TRUE FALSE FALSE FALSE FALSE FALSE FALSE -497.3750 1001.3741
## 2 TRUE TRUE FALSE TRUE FALSE FALSE FALSE FALSE -482.2418 977.7317
## 3 TRUE TRUE FALSE TRUE FALSE FALSE TRUE FALSE -468.8080 957.4882
## 4 TRUE TRUE FALSE TRUE TRUE FALSE FALSE TRUE -462.1527 950.8016
## 5* TRUE TRUE FALSE TRUE TRUE FALSE TRUE TRUE -453.2277 939.5758
## 6 TRUE TRUE TRUE TRUE TRUE FALSE TRUE TRUE -452.7801 945.3046
## 7 TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE -452.6330 951.6344요소 BestModel에는 lm 객체 형태로 최적 모형의 적합 결과가 입력되어 있다.
fit_bic$BestModel
##
## Call: glm(formula = y ~ ., family = family, data = Xi, weights = weights)
##
## Coefficients:
## (Intercept) k5 age wcyes lwg inc
## 2.90193 -1.43180 -0.05853 0.87237 0.61568 -0.03368
##
## Degrees of Freedom: 752 Total (i.e. Null); 747 Residual
## Null Deviance: 1030
## Residual Deviance: 906.5 AIC: 918.5AIC에 의한 선택 결과도 확인해 보자.
객체 fit_aic에도 동일한 방식으로 결과가 입력되어 있다.
fit_aic$Subsets
## Intercept k5 k618 age wc hc lwg inc logLikelihood AIC
## 0 TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE -514.8732 1029.7464
## 1 TRUE TRUE FALSE FALSE FALSE FALSE FALSE FALSE -497.3750 996.7500
## 2 TRUE TRUE FALSE TRUE FALSE FALSE FALSE FALSE -482.2418 968.4836
## 3 TRUE TRUE FALSE TRUE FALSE FALSE TRUE FALSE -468.8080 943.6160
## 4 TRUE TRUE FALSE TRUE TRUE FALSE FALSE TRUE -462.1527 932.3053
## 5* TRUE TRUE FALSE TRUE TRUE FALSE TRUE TRUE -453.2277 916.4554
## 6 TRUE TRUE TRUE TRUE TRUE FALSE TRUE TRUE -452.7801 917.5602
## 7 TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE -452.6330 919.2659fit_aic$BestModel
##
## Call: glm(formula = y ~ ., family = family, data = Xi, weights = weights)
##
## Coefficients:
## (Intercept) k5 age wcyes lwg inc
## 2.90193 -1.43180 -0.05853 0.87237 0.61568 -0.03368
##
## Degrees of Freedom: 752 Total (i.e. Null); 747 Residual
## Null Deviance: 1030
## Residual Deviance: 906.5 AIC: 918.5두 방법으로 동일한 변수가 선택된 것을 알 수 있다.
만일 설명변수가 많은 경우에는 BestModel를 구성하고 있는 설명변수의 이름을 추출해서 비교하는 것이 더 편리할 수 있다.
fit_aic$BestModel$term |> attr("term.labels") |> sort()
## [1] "age" "inc" "k5" "lwg" "wc"
fit_bic$BestModel$term |> attr("term.labels") |> sort()
## [1] "age" "inc" "k5" "lwg" "wc"- Stepwise selection
함수 MASS::stepAIC()를 사용하여 stepwise selection에 의한 변수선택을 진행해 보자.
진행 과정은 선형회귀모형의 경우와 동일하다.
library(MASS)
fit_null <- glm(lfp ~ 1, family = binomial, Mroz)
fit_full <- glm(lfp ~ ., family = binomial, Mroz)AIC에 의한 단계적 선택을 진행해 보자.
BIC에 의한 단계적 선택을 진행해 보자.
fit3 <- stepAIC(fit_null, scope = list(upper = fit_full, lower = fit_null),
trace = FALSE, k = log(nrow(Mroz)))네 가지 방법이 모두 동일한 결과를 보여주고 있다.
fit1$term |> attr("term.labels") |> sort()
## [1] "age" "inc" "k5" "lwg" "wc"
fit2$term |> attr("term.labels") |> sort()
## [1] "age" "inc" "k5" "lwg" "wc"
fit3$term |> attr("term.labels") |> sort()
## [1] "age" "inc" "k5" "lwg" "wc"
fit4$term |> attr("term.labels") |> sort()
## [1] "age" "inc" "k5" "lwg" "wc"- Lasso 모형 적합
함수 glmnet::glmnet()를 사용하여 lasso 모형을 적합해 보자.
설명변수로 이루어진 행렬을 함수 model.matrix()를 이용하여 생성하자.
최적 \(\lambda\) 값에 의한 로지스틱 lasso 모형을 함수 cv.glmnet()으로 적합해 보자.
로지스틱 모형의 설정은 family = "binomial"을 지정함으로써 가능하며,
type.measure로 CV error measure를 지정할 수 있다.
로지스틱 모형에서 디폴트 measure는 "deviance"이며, 2.5절에서 살펴볼 분류 성능을 평가하는 측도 중 misclassification error는 "class", ROC curve의 면적은 "auc"를 지정하면 사용할 수 있다.
library(glmnet)
set.seed(123)
cvfit_Mroz <- cv.glmnet(X_Mroz, Mroz$lfp,
family = "binomial",
type.measure = "deviance")CV error에 대한 결과를 모형 cvfit_Mroz의 내용과 그래프로 확인해 보자.
cvfit_Mroz
##
## Call: cv.glmnet(x = X_Mroz, y = Mroz$lfp, type.measure = "deviance", family = "binomial")
##
## Measure: Binomial Deviance
##
## Lambda Index Measure SE Nonzero
## min 0.001766 45 1.221 0.02598 7
## 1se 0.026225 16 1.243 0.02073 5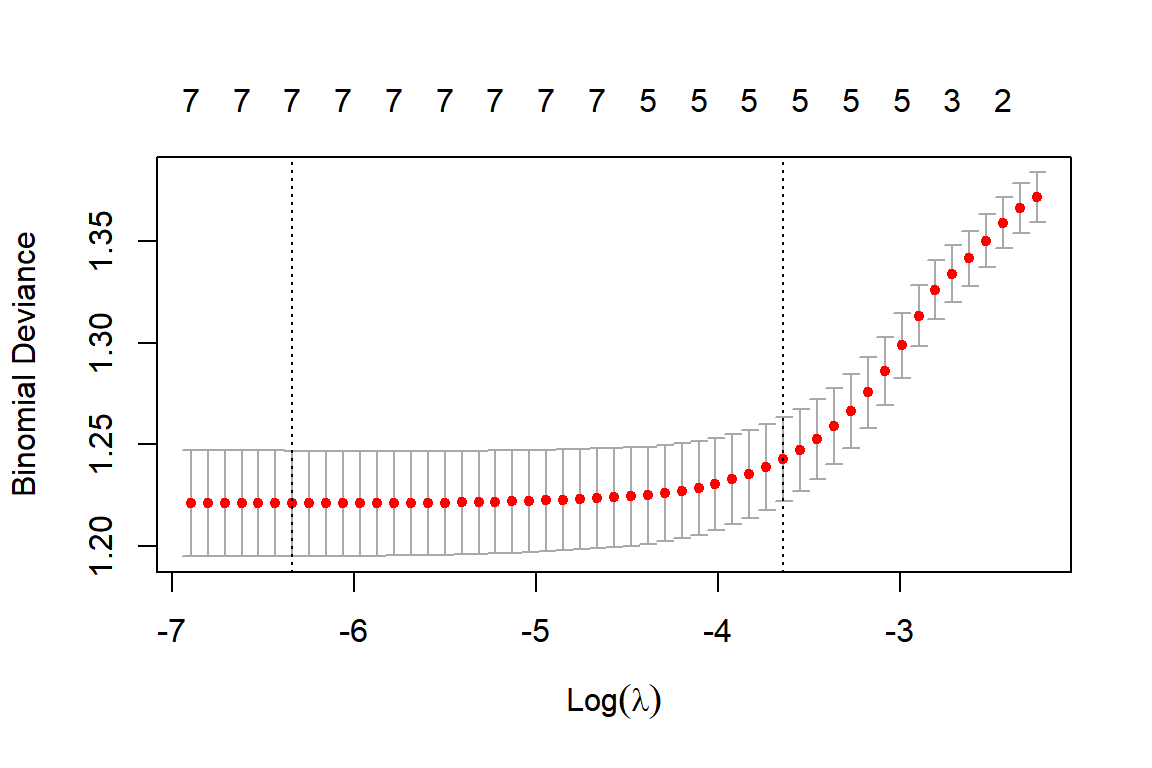
그림 2.6: lambda의 변화에 따른 CV error의 변화
최적 \(\lambda\) 값으로 lasso 모형의 회귀계수 추정 결과를 확인해 보자.
coef(cvfit_Mroz)
## 8 x 1 sparse Matrix of class "dgCMatrix"
## s1
## (Intercept) 1.54013397
## k5 -0.88490744
## k618 .
## age -0.02985041
## wcyes 0.46525473
## hcyes .
## lwg 0.40095168
## inc -0.01694822Best subset selection과 stepwise selection, 그리고 lasso 모형 모두 동일한 변수를 선택했다. 선택된 변수로 이루어진 모형은 다음과 같다.
fit1
##
## Call: glm(formula = lfp ~ k5 + age + lwg + inc + wc, family = binomial,
## data = Mroz)
##
## Coefficients:
## (Intercept) k5 age lwg inc wcyes
## 2.90193 -1.43180 -0.05853 0.61568 -0.03368 0.87237
##
## Degrees of Freedom: 752 Total (i.e. Null); 747 Residual
## Null Deviance: 1030
## Residual Deviance: 906.5 AIC: 918.5로지스틱 회귀모형을 구성하고 있는 개별 설명변수들의 효과는 odds ratio로 설명할 수 있지만,
그래프로 표현할 수 있다면 훨씬 효과적일 것이다.
모형 fit1에서 설명변수 k5와 wc가 반응변수 lfp가 "yes"가 될 확률에 미치는 영향을 그래프로 표현해 보자.
다른 설명변수 age, lwg와 inc는 각 변수의 평균값으로 고정하고,
wc가 각각 "yes"와 "no"일 때, k5의 값이 0에서 4로 증가함에 따라 lfp가 "yes"가 될 확률이 어떻게 변화하는지 그래프로 나타내 보자.
먼저 확률 예측에 사용될 새로운 데이터를 구성해 보자.
df1 <- Mroz |>
summarise(across(c(age,lwg,inc), mean)) |>
expand_grid(k5 = 0:4, wc = c("yes", "no")
)df1
## # A tibble: 10 × 5
## age lwg inc k5 wc
## <dbl> <dbl> <dbl> <int> <chr>
## 1 42.5 1.10 20.1 0 yes
## 2 42.5 1.10 20.1 0 no
## 3 42.5 1.10 20.1 1 yes
## 4 42.5 1.10 20.1 1 no
## 5 42.5 1.10 20.1 2 yes
## 6 42.5 1.10 20.1 2 no
## 7 42.5 1.10 20.1 3 yes
## 8 42.5 1.10 20.1 3 no
## 9 42.5 1.10 20.1 4 yes
## 10 42.5 1.10 20.1 4 no이제 df1에 주어진 설명변수의 값에 대하여 lfp가 "yes"가 될 확률을 예측하고, 그 결과를 막대그래프로 나타내 보자.
df1 |>
mutate(p1 = predict(fit1, newdata = df1,
type = "response")) |>
ggplot() +
geom_col(aes(x = k5, y = p1, fill = wc),
position = "dodge") +
labs(y = "Prob") 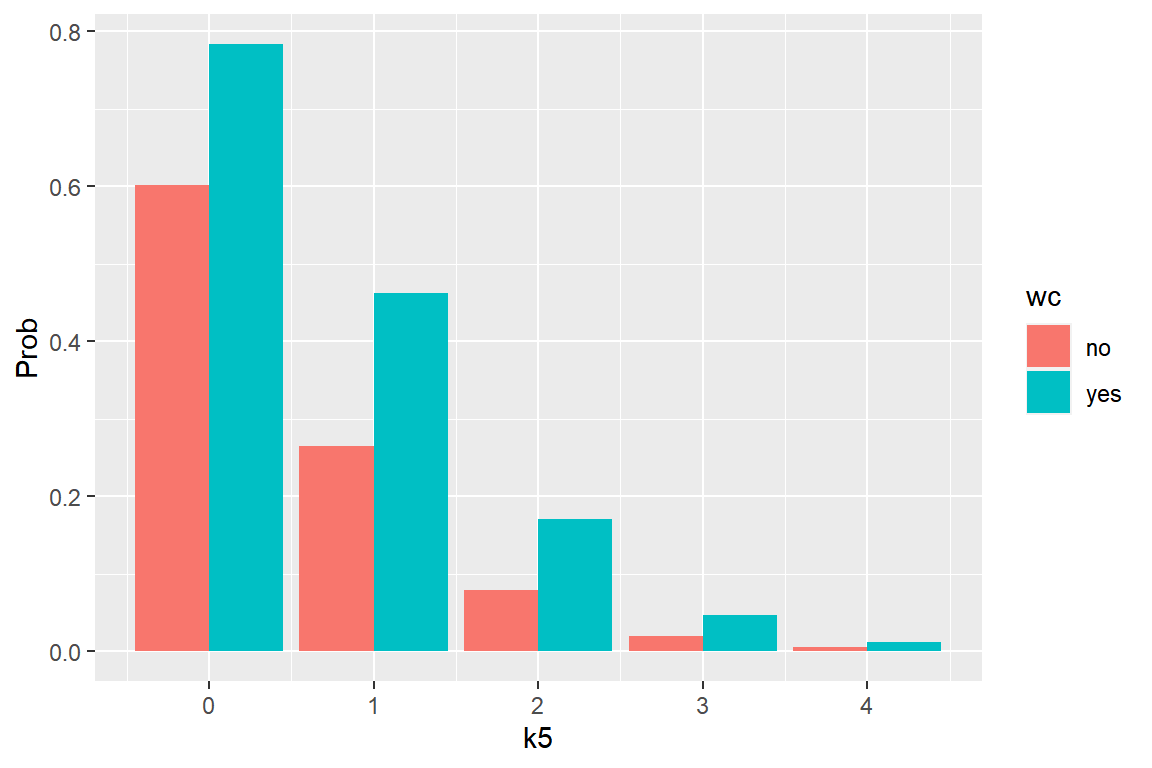
그림 2.7: k5와 wc의 값에 따른 lfp가 'yes'가 될 확률의 변화
k5의 값이 증가함에 따라 직업을 가질 확률이 매우 급격하게 감소하는 것을 볼 수 있다.
또한 여성의 대학과정 등록한 여부가 직업을 가질 확률이 큰 영향을 주고 있음도 확인할 수 있다.
이번에는 모형 fit1에서 설명변수 k5와 wc, 그리고 lwg의 영향력을 그래프로 표현해 보자.
설명변수 age와 inc는 평균으로 고정하고,
wc가 각각 "yes"와 "no"이고, k5의 값이 0~3이며, lwg가 (-2,3)의 값을 갖을 때,
lfp가 "yes"가 될 확률이 어떻게 변화하는지 그래프로 나타내 보자.
먼저 확률 예측에 사용될 새로운 데이터를 구성해 보자.
df2 <- Mroz |>
summarise(across(c(age, inc), mean)) |>
expand_grid(k5 = 0:3, wc = c("yes", "no"),
lwg = seq(-2, 3, length = 50)
)이제 df2에 주어진 설명변수의 값에 대하여 lfp가 "yes"가 될 확률을 예측하고, 그 결과를 선그래프로 나타내 보자.
df2 |>
mutate(p2 = predict(fit1, newdata = df2,
type = "response")) |>
ggplot() +
geom_line(aes(x = lwg, y = p2, color = factor(k5)),
linewidth = 1) +
facet_wrap(vars(wc)) +
labs(color = "Number of Kids", y = NULL) +
ylim(0,1)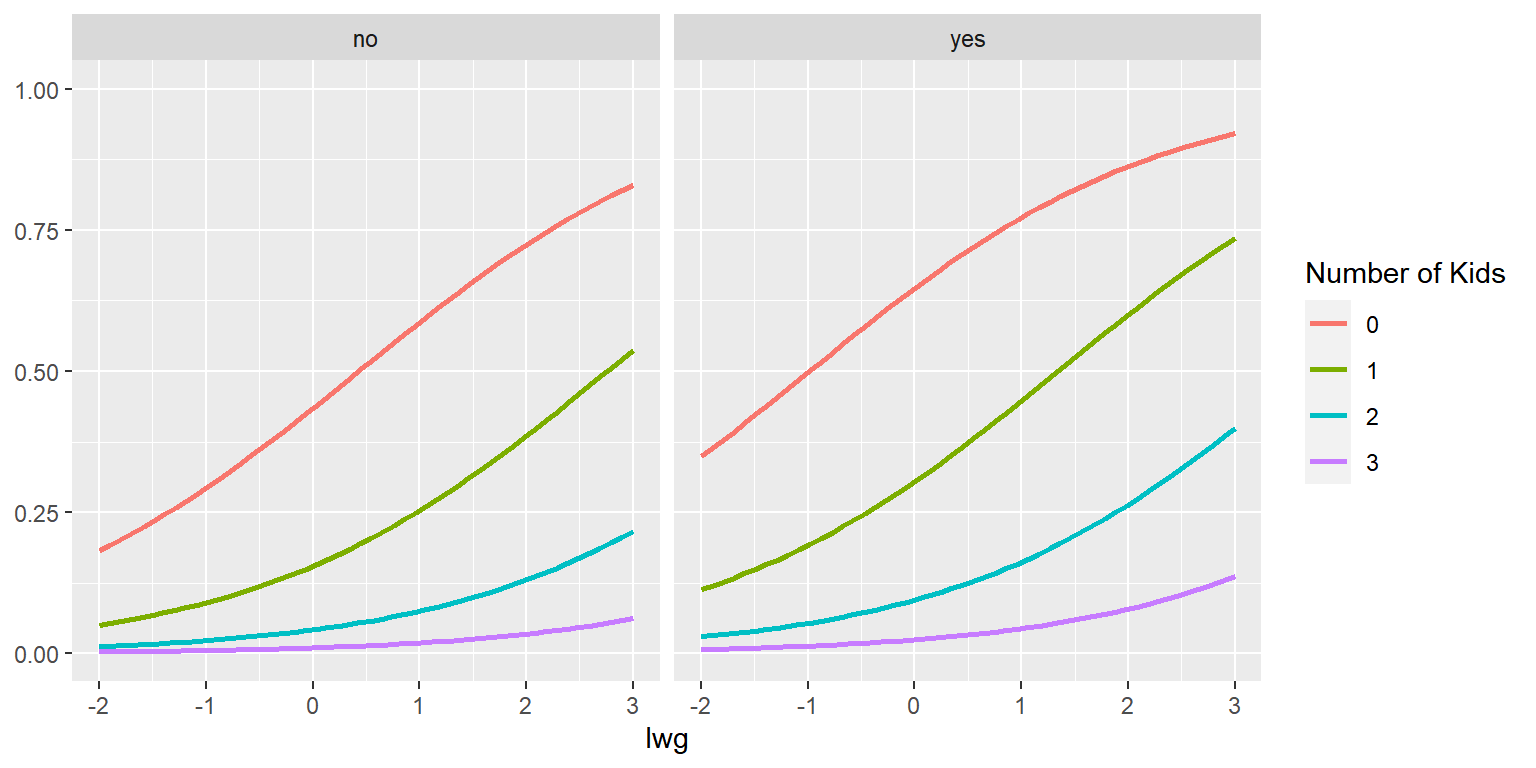
그림 2.8: k5, wc와 lwg의 값에 따른 lfp가 'yes'가 될 확률의 변화
변수 lwg의 값에 따른 lfp가 "yes"가 될 확률을 선그래프로 표시하되, k5의 값에 따라 다른 색으로 표시했으며, 변수 wc는 faceting으로 효과를 비교했다.
그림 2.8와 같은 facet 그래프는 faceting 변수의 각 범주 내에서의 효과 비교는 수월하게 이루지지만, 범주 간의 효과 비교는 조금 어려운 측면이 있다. 예를 들어, wc가 "no"인 그룹과 "yes"인 그룹에서 k5가 0에 해당하는 두 곡선의 직접적인 비교가 어렵다는 것이다.
따라서 변수 wc의 효과를 다르게 나타낼 수 있는 그래프를 함께 작성하는 것이 필요할 것이다.
wc를 시각적 요소 linetype에 매핑한 그래프를 작성해 보자.
df2 |>
mutate(p2 = predict(fit1, newdata = df2,
type = "response")) |>
ggplot() +
geom_line(aes(x = lwg, y = p2,
color = factor(k5), linetype = wc),
linewidth = 1) +
labs(color = "Number of Kids", linetype = "WC",
y = NULL) +
ylim(0,1)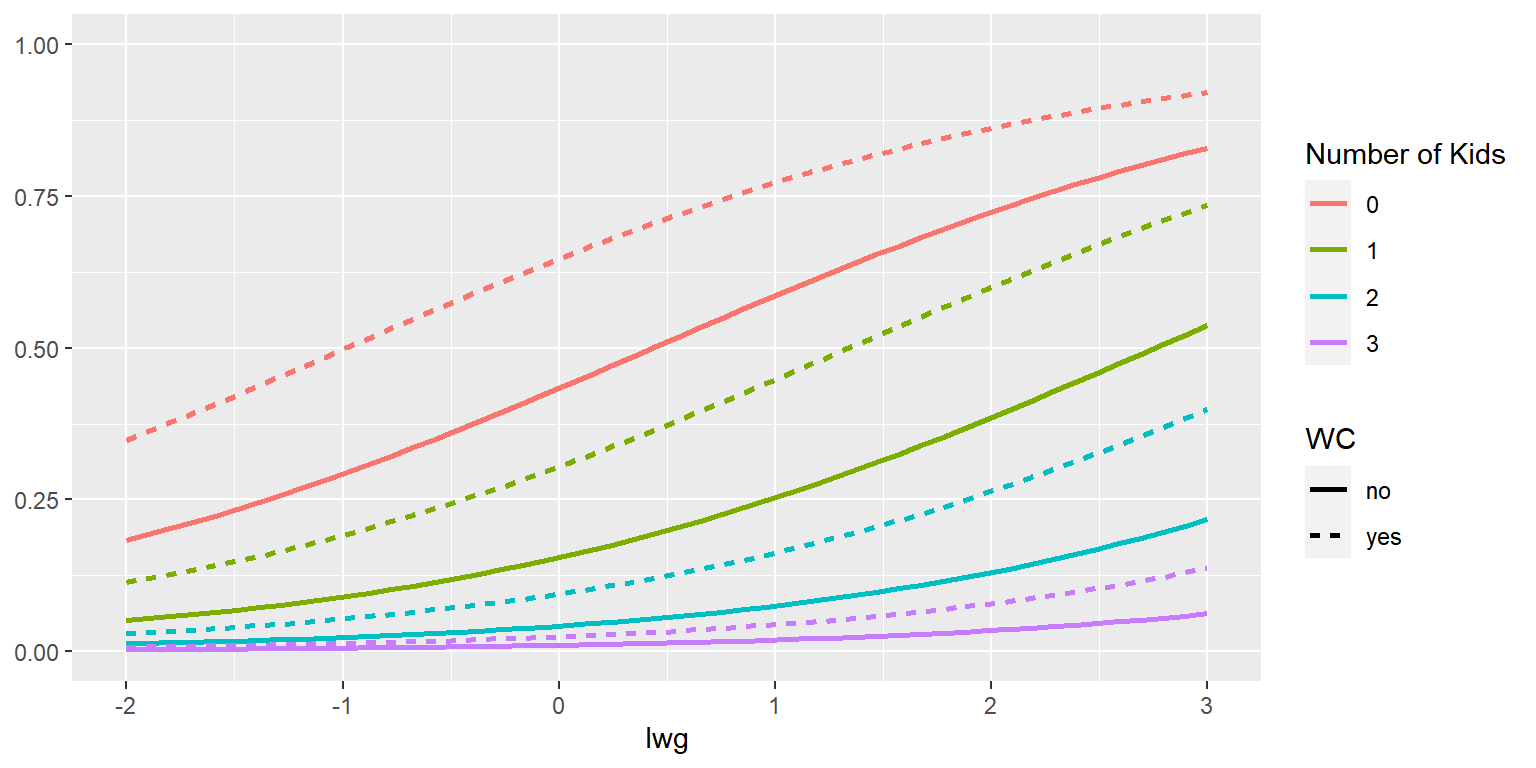
그림 2.9: k5, wc와 lwg의 값에 따른 lfp가 'yes'가 될 확률의 변화
이번에는 모형 fit1에서 설명변수 k5와 inc, 그리고 lwg의 영향력을 그래프로 표현해 보자.
설명변수 age는 평균으로, wc는 "yes"인 경우로 고정하자.
k5의 값이 0, 1, 2, 3이며, lwg가 (-2, 3)의 값을 갖고, inc가 (0, 30)의 값을 갖을 때,
lfp가 "yes"가 될 확률이 어떻게 변화하는지 그래프로 나타내 보자.
먼저 확률 예측에 사용될 새로운 데이터를 구성해 보자.
df3 <-
Mroz |>
summarise(age = mean(age), wc = "yes") |>
expand_grid(k5 = 0:3, inc = seq(0, 30, length = 50),
lwg = seq(-2, 3, length = 50)
)연속형 변수 inc와 lwg의 값에 따라 lfp가 "yes"가 될 확률의 변화를 함께 나타낼 수 있는 그래프에는 Heatmap이 있으며, 함수 geom_raster()로 작성할 수 있다.
변수 k5의 효과는 faceting으로 나타내 보자.
df3 |>
mutate(p3 = predict(fit1, newdata = df3,
type = "response")) |>
ggplot() +
geom_raster(aes(x = lwg, y = inc, fill = p3)) +
scale_fill_viridis_c() +
facet_wrap(vars(k5), labeller = "label_both") +
labs(fill = "P(Y=1)")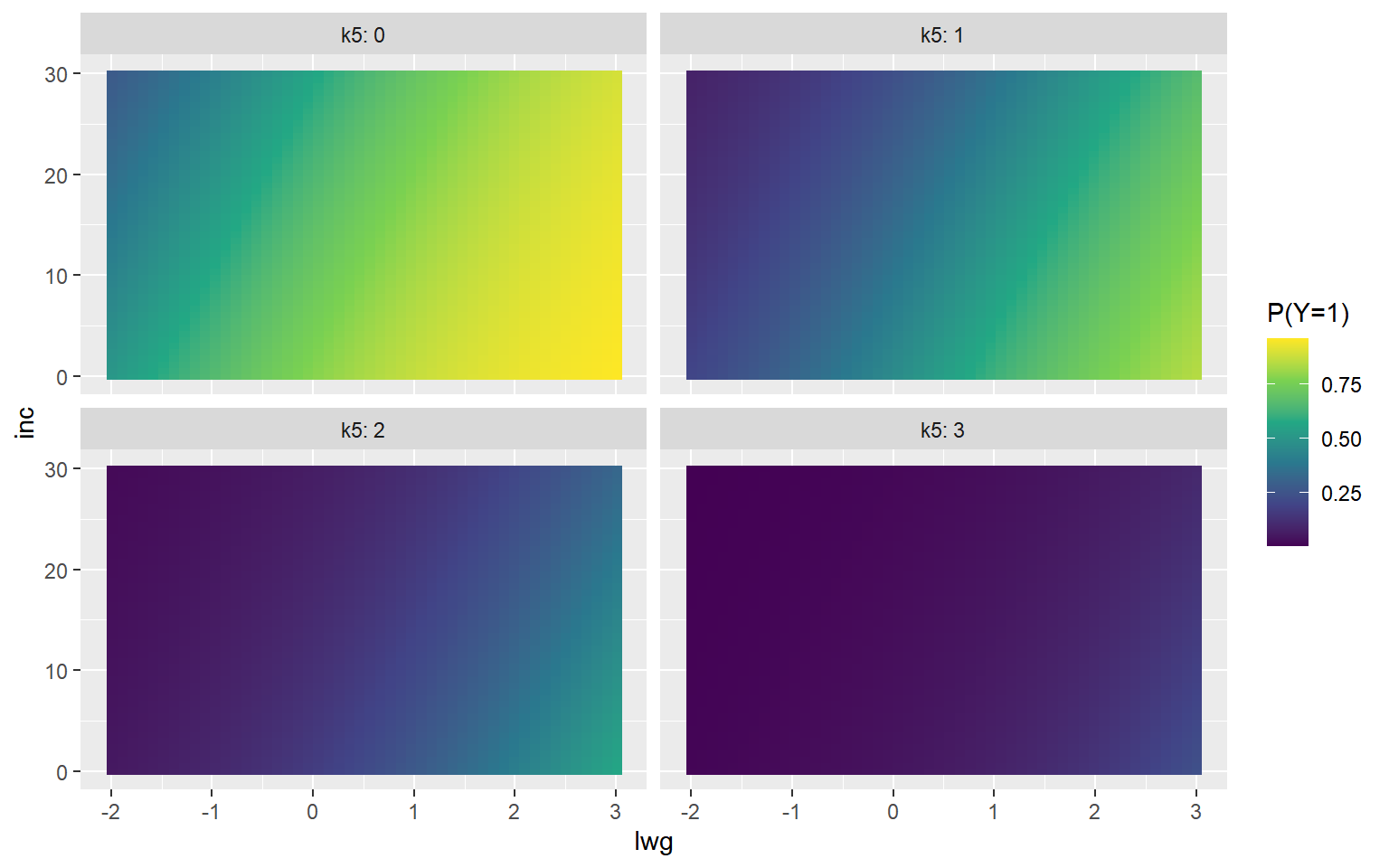
그림 2.10: k5, inc와 lwg의 값에 따른 lfp가 'yes'가 될 확률의 변화
변수 inc의 값이 낮아지고 lwg의 값이 증가함에 따라 lfp가 "yes"가 될 확률이 높아지고 있지만,
k5의 값이 상승함에 따라 확률은 전반적으로 크게 떨어지는 것을 볼 수 있다.
2.4 회귀진단
선형회귀모형의 경우와 같이 로지스틱 회귀모형에서도 적합한 모형에 대한 회귀진단을 실시해야 한다. 선택한 모형이 주어진 자료를 잘 설명하고 있는지에 대한 확인이 필요한 것이다. 다만 선형회귀모형의 회귀진단에서 주로 사용됐던 잔차와는 조금 다른 형태의 잔차가 로지스틱 회귀모형에서 사용된다는 차이가 있다.
선형회귀모형에서 잔차 \(e_{i}=\hat{y}_{i}-y_{i}\) 는 회귀모형의 오차 \(\varepsilon_{i}\) 를 대신하는 역할을 하고 있지만, 로지스틱 회귀모형에서는 선형회귀모형처럼 가법모형 방식의 오차를 정의할 수 없다는 문제가 있다. 따라서 로지스틱 회귀모형에서 잔차의 의미는 조금 다를 수밖에 없다.
로지스틱 회귀모형에서 사용되는 잔차에는 Pearson 잔차와 deviance 잔차가 있다. 먼저 Pearson 잔차 \(r_{i}^{P}\) 는 다음과 같이 정의된다.
\[\begin{equation} r_{i}^{P}=\frac{y_{i}-\hat{\pi}_{i}}{\sqrt{\hat{\pi}_{i}(1-\hat{\pi}_{i})}} \end{equation}\]
단, \(\hat{\pi}_{i}\) 는 \(\pi_{i} = P(Y_{i}=1|X)\) 의 추정값이다.
Deviance 잔차 \(r_{i}^{D}\) 는 다음과 같이 정의된다.
\[\begin{equation} r_{i}^{D}=s_{i}\sqrt{-2 \left(y_{i}\log \hat{\pi}_{i} + (1-y_{i}) \log (1-\hat{\pi}_{i}) \right)} \end{equation}\]
단, \(s_{i}\) 는 \(y_{i}=1\) 이면 1이고, \(y_{i}=0\) 이면 0이다.
두 잔차의 제곱합은 모두 모형의 적합도를 나타내는 통계량이 된다. 회귀진단 과정에서는 잔차의 분포를 조금 더 좌우대칭에 가깝게 변형을 하기 위해 표준화를 시킨 잔차를 사용하기도 한다. 표준화 Pearson 잔차는 \(r_{i}^{P}/\sqrt{1-h_{i}}\) 로 정의되고, 표준화 deviance 잔차는 \(r_{i}^{D}/\sqrt{1-h_{i}}\) 로 정의된다. 단, \(h_{i}\) 는 \(i\) 번째 관찰값의 leverage이다.
영향력이 큰 관찰값의 탐지도 선형회귀모형의 경우와 유사한 방식으로 진행한다. Cook’s distance와 leverage가 중요한 통계량으로 사용된다. 다중공선성의 존재 여부도 선형회귀모형의 경우와 동일하게 확인할 필요가 있다.
\(\bullet\) 예제:carData::Mroz
2.3절에서 수행된 모든 변수선택은 동일한 모형을 결과로 보여주었다. 선정된 모형을 대상으로 회귀진단을 실시해 보자.
fit_full <- glm(lfp ~ ., family = binomial, Mroz)
fit1 <- MASS::stepAIC(fit_full, direction = "both", trace = FALSE)먼저 모형 fit1의 잔차 산점도를 작성해 보자.
로지스틱 회귀모형에 대한 잔차 산점도는 패키지 car의 함수 residualPlots()로 작성할 수 있다.
디폴트 잔차는 Pearson 잔차이며, deviance 잔차를 원하는 경우에는 type = "deviance"를 추가하면 된다.
실행 결과로 각 설명변수와 Pearson 잔차 (또는 deviance 잔차)의 산점도가 작성되는데, 설명변수가 요인인 경우에는 상자그림이 작성된다. 또한 설명변수의 선형결합인 \(\hat{\beta}_{0} + \hat{\beta}_{1}x_{1} + \cdots + \hat{\beta}_{k}x_{k}\) 와 잔차의 산점도가 마지막 그래프로 작성된다.
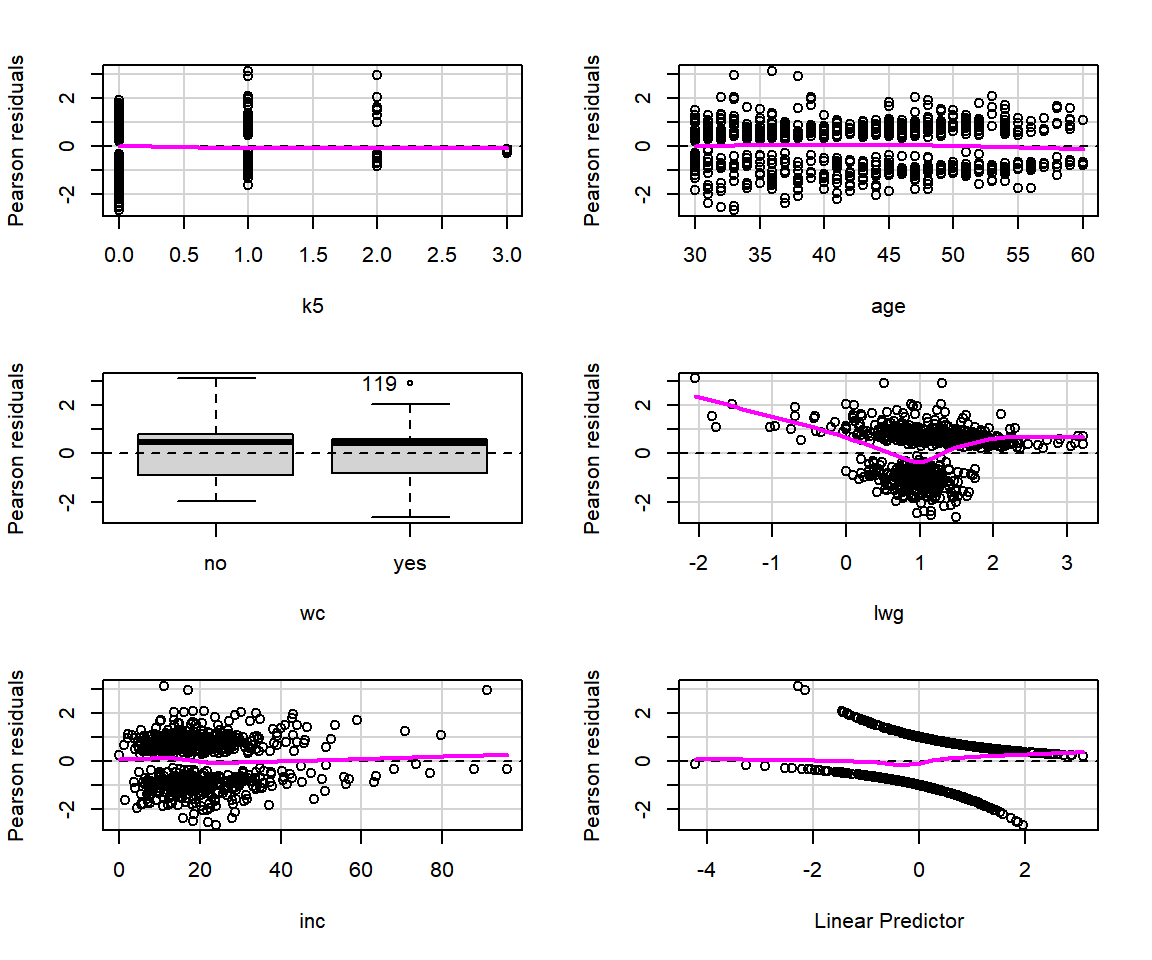
그림 2.11: 함수 residualPlots()에 의한 회귀진단
## Test stat Pr(>|Test stat|)
## k5 0.1102 0.73990
## age 0.6284 0.42793
## wc
## lwg 152.7522 < 2e-16 ***
## inc 3.2493 0.07145 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1그림 2.11에서 볼 수 있는 잔차 산점도는 선형회귀모형의 경우처럼 0을 중심으로 일정한 폭의 영역에 무작위로 흩어져 있는 것과는 많이 다른 모습이다.
그것은 반응변수가 0이면 잔차가 음수가 되고, 반응변수가 1이면 양수가 되는 관계가 있기 때문이다.
각 패널에 추가된 마젠타(magenta) 색의 실선은 국소다항회귀를 나타내는 것으로서 0 근처에서 수평선을 유지해야 한다.
만일 명백한 곡선의 형태가 나타난다면 해당 변수의 적합에 문제가 있음을 보여주는 것이 된다.
만일 표준화 Pearson 잔차나 스튜던트화 Pearson 잔차를 대신 사용하고자 한다면 type = "rstandard" 또는 type = "rstudent"를 입력하면 된다.
그래프와 더불어 출력된 검정 결과는 숫자형 변수의 curvature test로서, 각 설명변수의 2차항을 추가한 각각의 모형에서 추가된 2차항 변수의 유의성을 검정한 것이다.
변수 lwg의 경우, 추가된 2차항이 유의한 것으로 나타났는데, 잔차 산점도에서도 곡선이 나타난 것으로 보아 2차항을 모형에 포함시켜 확인할 필요가 있는 것으로 보인다.
기존의 모형에 변수를 추가하거나 제외하는 작업은 함수 update()로 하는 것이 더 편리하다.
모형 fit1을 대상으로 기존의 모형(. ~ .)에 I(lwg^2)을 추가(. ~ . + I(lwg^2))하는 것이 된다.
summary(fit2)
##
## Call:
## glm(formula = lfp ~ k5 + age + wc + lwg + inc + I(lwg^2), family = binomial,
## data = Mroz)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 6.518168 0.821533 7.934 2.12e-15 ***
## k5 -1.527347 0.223132 -6.845 7.65e-12 ***
## age -0.068245 0.012794 -5.334 9.61e-08 ***
## wcyes 0.139512 0.239424 0.583 0.560097
## lwg -7.763915 1.094941 -7.091 1.33e-12 ***
## inc -0.033799 0.008864 -3.813 0.000137 ***
## I(lwg^2) 4.580429 0.566054 8.092 5.88e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1029.7 on 752 degrees of freedom
## Residual deviance: 753.7 on 746 degrees of freedom
## AIC: 767.7
##
## Number of Fisher Scoring iterations: 7모형에 추가된 lwg의 2차항은 유의한 것으로 나타났는데,
변수를 추가함으로 해서 모형의 적합도가 얼마나 향상됐는지는 모형의 AIC와 BIC를 비교해 보면 알 수 있다.
또한 이 변수가 추가되면서 wc가 비유의적인 변수가 되었는데,
모형의 적합도에는 큰 차이가 있을 것으로 보이지는 않지만 비유의적인 변수를 제외한 모형도 비교해 보자.
AIC와 BIC에서 fit2와 fit3는 차이가 없는 모형임을 알 수 있다.
영향력이 큰 관찰값의 탐지는 패키지 car의 함수 influencePlot()으로 할 수 있다.
사용법 및 해석 방식은 선형회귀모형의 경우와 동일하다.
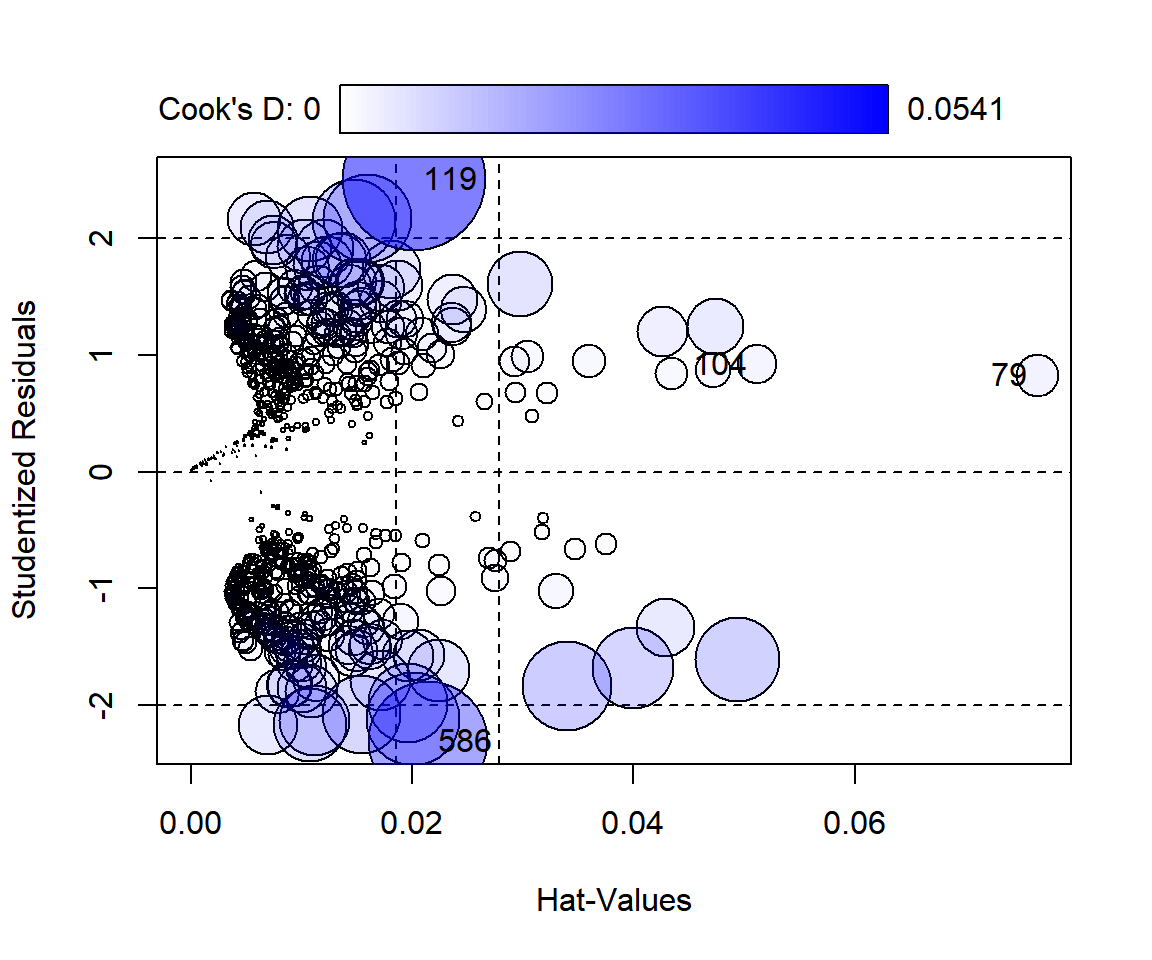
그림 2.12: 함수 influencePlot()에 의한 회귀진단 그래프
## StudRes Hat CookD
## 79 0.8256292 0.07649726 0.004919585
## 104 0.9178673 0.05114926 0.004084955
## 119 2.5033037 0.02013335 0.054106915
## 586 -2.3107567 0.02148102 0.037489575다중공선성의 문제도 패키지 car의 함수 vif()로 확인해 보자.
변수 lwg와 I(lwg^2)의 VIF 값이 크게 나왔는데, 이것은 다항회귀모형에서 나타나는 자연스러운 현상으로 볼 수 있다.
2.5 분류성능 평가
로지스틱 회귀모형은 분류 모형으로 매우 광범위하게 사용되고 있다. 이 절에서는 로지스틱 회귀모형의 분류성능을 평가하는 몇 가지 측도에 대해 살펴보도록 하자.
변수선택과 회귀진단 과정을 통해 최적 로지스틱 회귀모형이 선정되면, 반응변수가 “성공” 범주에 속할 확률 \(\pi(\mathbf{x}) = P(Y=1|\mathbf{x})\) 을 추정할 수 있게 된다. 이어서 추정된 확률 \(\hat{\pi}(\mathbf{x})\) 를 이용하여 각 관찰값을 다음과 같이 두 범주로 분류할 수 있게 된다.
\[\begin{equation} \hat{y} = \begin{cases} 0, & \quad \text{if}~~ \hat{\pi}(\mathbf{x}) < d \\ 1, & \quad \text{if}~~ \hat{\pi}(\mathbf{x}) \geq d \end{cases} \end{equation}\]
분류기준값 \(d\) 는 0.5로 놓고 분류를 시행하는 것이 일반적이다.
분류성능을 평가하기 위한 첫 번째 단계는 관찰값 \(y\) 와 예측값 \(\hat{y}\) 의 2차원 분할표인 confusion matrix를 작성하는 것이다. \(n\) 개의 자료를 대상으로 분류 작업을 실행하여 \(y=0\) 인 자료 중에 \(\hat{y} = 0\) 또는 \(\hat{y} = 1\) 로 각각 분류된 자료의 개수와 \(y=1\) 인 자료 중에 \(\hat{y} = 0\) 또는 \(\hat{y} = 1\) 로 각각 분류된 자료의 개수를 2차원 분할표 형태로 작성한 것이 confusion matrix이다.
표 2.1은 Machine Learning 분야에서 사용되는 용어를 사용하여 작성된 confusion matrix이다. Machine Learning 분야에서는 일반적으로 ‘성공’ 범주를 Event로, ‘실패’ 범주를 NonEvent로 표시를 한다. 또한 ‘성공’ 범주로 분류하면 Positive, ‘실패’ 범주로 분류하면 Negative로 표현하며, 분류 결과가 맞으면 True, 틀리면 False로 표현한다. 따라서 \(y=0\) 인 자료를 \(\hat{y} = 0\) 분류하면 True Negative(TN), \(\hat{y} = 1\) 분류하면 False Positive(FP)로 표현하고, \(y=1\) 인 자료를 \(\hat{y} = 0\) 로 분류하면 False Negative(FN), \(\hat{y} = 1\) 로 분류하면 True Positive(TP)로 표현한다.
| Prediction | NonEvent | Event |
|---|---|---|
| NonEvent | True Negative | False Negative |
| Event | False Positive | True Positive |
2.5.1 분류성능 평가 측도
1) 정분류율(Accuracy rate)
정분류율은 예측값이 관찰값과 동일한 범주로 분류된 비율을 나타내는 것이다. 표 2.1의 confusion matrix에서는 \((TN + TP)/n\) 으로 표현된다.
정분류율은 모형의 분류성능에 대한 기본적인 평가 측도로 사용되고 있으나, 문제점이 있는 평가 측도이어서 조심해서 사용해야 한다. 첫 번째 문제로 지적되는 것은 더 많이 관측된 범주의 비율보다 정분류율이 더 높아야 의미가 있는 측도가 된다는 점이다. 예를 들어 Event로 100개의 자료가 관측되었고, NonEvent로 50개의 자료가 관측된 경우에, 총 150개 자료를 모두 Positive로 단순 분류해도 정분류율은 100/150 = 0.67이 된다. 따라서 모형에 의한 정분류율이 더 많이 관측된 범주의 비율(No information rate)보다 작다면 사용할 의미가 없어지는 것이다.
두 번째 문제는 분류에서 발생되는 두 가지 오류에 대한 정보를 전혀 얻을 수 없는 측도라는 점이다. 두 가지 분류 오류인 False Positive와 False Negative로 인한 cost가 다른 경우에 정분류율만으로 분류 결과를 평가하기 어렵다는 문제이다. 예를 들어 스팸 메일에 대한 분류 작업을 하는 경우, 중요한 메일이 스팸으로 분류되는 False Positive가 훨씬 중요한 오류가 될 것이다. 이런 경우 정분류율에서 발생되는 약간의 불이익을 감소하더라도 False Positive가 더 낮은 분류 모형을 사용하는 것이 바람직할 것이다.
2) 민감도(Sensitivity)와 특이도(Specificity)
민감도는 Event로 관측된 자료 중 Positive로 분류된 자료의 비율을 의미한다.
\[\begin{equation} sensitivity = \frac{TP}{FN+TP} \end{equation}\]
민감도를 True Positive rate라고 할 수 있는데, 그것은 Event 범주에서 Positive로 잘 분류된 비율이기 때문이다.
특이도는 NonEvent로 관측된 자료 중 Negative로 분류된 자료의 비율을 의미한다.
\[\begin{equation} specificity = \frac{TN}{TN+FP} \end{equation}\]
NonEvent 범주에서 Positive로 잘못 분류되는 비율을 False Positive 비율이라고 한다면, 특이도는 1-False Positive rate가 된다.
민감도와 특이도는 한쪽이 증가하면 다른 쪽은 감소하는 trade-off의 관계를 가지고 있다. True Positive를 높이는 것이 더 중요한 상황이라면 민감도를 판단 기준으로 사용해야하지만, False Positive를 낮추는 것이 더 중요한 상황이라면 특이도를 판단 기준으로 사용해야 할 것이다. 따라서 True Positive와 False Positive의 상대적 중요도를 고려해서 분류기준점을 조절하는 것이 필요하다.
3) Precision과 F1 score
Precision은 Positive로 분류한 자료 중 Event 자료의 비율을 나타낸다.
\[\begin{equation} precision = \frac{TP}{TP+FP} \end{equation}\]
F1 score는 Precision과 Recall이라고도 불리는 Sensitivity의 harmonic mean으로 정의된다.
\[\begin{equation} F1 = 2 \times \frac{precision \times recall}{precision + recall} \end{equation}\]
F1 score는 False Positive와 False Negative의 영향력이 모두 반영된 측도로 볼 수 있으며, 따라서 단순한 정분류율보다 더 유용하게 사용되고 있다.
4) ROC(Receiver Operating Characteristic) curve
ROC curve는 모든 분류 기준값 에 대해서 계산된 특이도와 민감도를 \((x,y)\) 좌표로 하여 작성된 그래프이다. 그림 2.13에 예시된 ROC curve를 볼 수 있다. 그래프의 좌측 하단은 분류기준값 \(d\) 를 1로 설정한 지점으로서 모든 자료가 Negative로 분류되었고, 따라서 민감도가 0, 특이도가 1이 된 것이다. 이제 분류 기준값을 조금씩 낮추게 되면 특이도가 떨어지는 대신 민감도는 높아지게 되는데, 분류 정확도가 높은 모형이라면 곡선의 기울기가 매우 급격하게 상승하게 된다. 즉, 특이도를 조금만 희생시키면 민간도가 급격하게 좋아지게 되어서 전반적인 분류 정확도를 높일 수 있는 것이다. 그래프의 우측 상단은 분류기준값을 0으로 설정한 지점으로서 모든 자료가 Positive로 분류되었고, 따라서 민감도는 1, 특이도는 0이 된 것이다.
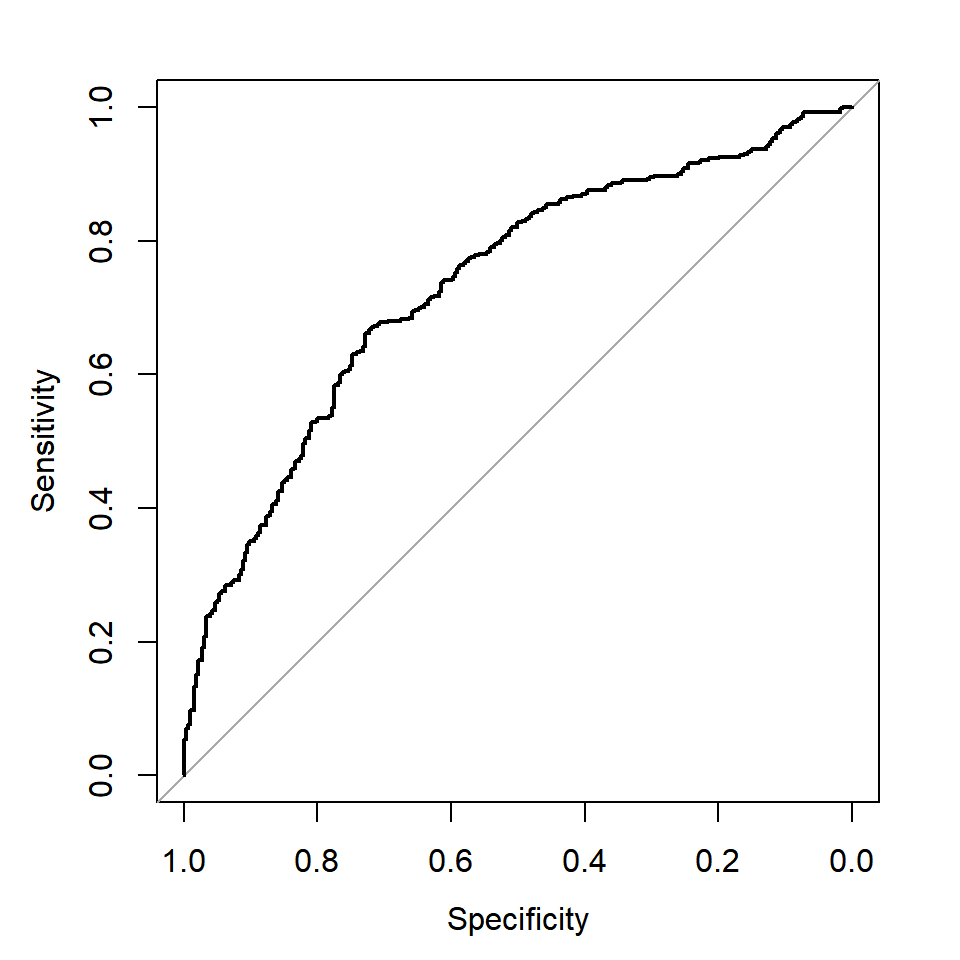
그림 2.13: ROC curve
ROC curve의 전반적인 모습을 보고 모형의 분류성능을 판단하는 것이 정확한 결론을 내는 방법이지만, 많은 분석을 실시하는 상황에서는 조금 더 간단한 방법이 필요하기도 한다. 분류 정확도가 높은 모형의 ROC curve는 기울기가 매우 급격하게 상승을 하는데, 이렇게 되면 ROC curve 아래 부분의 면적이 증가하게 된다. 따라서 ROC curve 아래 부분의 면적을 기준으로 분류 정확도를 판단하는 것이 가능한 것이다. ROC curve 아래 부분의 면적을 AUC(Area Under the Curve)라고 하며, AUC 값이 더 큰 모형이 선호된다.
ROC curve의 그래프에는 대부분 점선으로 대각선이 그려진다. 이 대각선에서는 민감도와 특이도 값을 더하면 1이 되는데, 이것은 True Positive rate이 False Positive rate과 같은 경우에 해당하는 상황이다. 즉, 분별력이 전혀 없는 모형이 되는 것이다. 만일 ROC curve가 대각선과 일치한다면 AUC는 0.5가 된다.
\(\bullet\) 분류성능 평가 측도를 위한 함수
지금까지 살펴본 분류성능 평가 측도 중 정분류율과 민감도, 특이도 및 F1 score 등은 패키지 caret의 함수 confusionMatrix()로 구할 수 있다.
함수 confusionMatrix()의 기본적인 사용법은 confusionMatix(data, reference, positive)이다.
data에는 예측 결과를 요인으로 지정하고, reference에는 반응변수를 요인으로 지정해야 한다.
positive에는 반응변수의 요인 수준 중에 Event에 해당하는 수준을 지정해야 한다.
ROC curve는 패키지 pROC의 함수 roc()로 작성할 수 있다.
함수 roc()의 기본적인 사용법은 roc(response, predictor, plot = TRUE, ... )이다.
response에는 반응변수의 벡터를 지정하는데, 유형은 요인, 숫자, 문자 모두 가능하다.
predictor에는 ‘성공’ 범주에 속할 확률이 계산된 벡터를 지정해야 한다.
ROC curve의 그래프를 작성하려면 옵션 plot에 TRUE를 지정해야 한다.
AUC의 계산은 roc 객체를 함수 auc()에 입력하면 계산된다.
\(\bullet\) 예제 carData::Mroz
데이터 프레임 Mroz의 변수 lfp를 반응변수로 하고 나머지 변수를 설명변수로 하는 로지스틱 회귀모형을 적합해 보자.
2.3절과 2.4절의 예제에서는 Mroz 자료를 모두 사용하여 분석을 실시하였다.
그러나 예측모형을 만드는 것이 목적인 경우에는 전체 자료를 반드시 training data와 test data로 분리하고,
training data만을 사용하여 ‘최적’ 모형을 적합해야 한다.
Test data는 모형 적합 과정에서는 절대로 사용되면 안 되고, 선택된 모형에 대한 평가 목적으로만 사용되어야 한다.
예측모형 적합을 위한 첫 번째 단계인 자료 분리는 함수 caret::createDataPartition()으로 하겠다.
이 함수는 연속형 반응변수의 예측 상황인 1.5절에서 이미 효과적으로 사용한 함수이다.
이항반응변수의 경우에는 반응변수의 두 범주의 비율이 전체 자료와 분리된 자료에서 모두 동일하게 유지되는 것이 필요한데, 이것은 층화추출이 이루어지면 가능하다.
함수 createDataPartition()에 요인이 첫 번째 변수로 입력되면 요인의 각 범주에 대한 층화추출이 이루어진다.
전체 자료의 80%를 training data로 분리하고, 20%의 자료는 test data로 분리하자.
library(tidyverse)
library(caret)
set.seed(123)
x.id <- createDataPartition(Mroz$lfp, p = 0.8, list = FALSE)[,1]
train_M <- Mroz |> slice(x.id)
test_M <- Mroz |> slice(-x.id)변수 lfp의 "yes"와 "no"의 비율을 Mroz와 train_M, test_M에서 각각 확인해 보자.
Mroz |> count(lfp) |> mutate(p = n/sum(n))
## lfp n p
## 1 no 325 0.4316069
## 2 yes 428 0.5683931
train_M |> count(lfp) |> mutate(p = n/sum(n))
## lfp n p
## 1 no 260 0.4311774
## 2 yes 343 0.5688226
test_M |> count(lfp) |> mutate(p = n/sum(n))
## lfp n p
## 1 no 65 0.4333333
## 2 yes 85 0.5666667이제 training data를 대상으로 ‘최적’ 모형을 적합을 위한 변수선택을 진행해 보자.
변수선택은 best subset selection과 stepwise selection을 사용할 것이며,
먼저 best subset selection 방법을 함수 bestglm()으로 수행해 보자.
library(bestglm)
fit1 <- bestglm(Xy, family = binomial)$BestModel
fit2 <- bestglm(Xy, family = binomial, IC = "AIC")$BestModel함수 stepAIC()로 stepwise selection에 의한 변수선택을 진행해 보자.
fit_full <- glm(lfp ~ ., family = binomial, train_M)
fit_null <- glm(lfp ~ 1, family = binomial, train_M)library(MASS)
fit3 <- stepAIC(fit_null, scope = list(upper = fit_full, lower = fit_null),
trace = FALSE)
fit4 <- stepAIC(fit_full, direction = "both", trace = FALSE)
fit5 <- stepAIC(fit_null, scope = list(upper = fit_full, lower = fit_null),
trace = FALSE, k = log(nrow(train_M)))
fit6 <- stepAIC(fit_full, direction = "both", trace = FALSE, k = log(nrow(train_M)))선택된 모형의 변수선택 결과를 확인해 보자.
fit1$terms |> attr("term.labels") |> sort()
## [1] "age" "inc" "k5" "lwg" "wc"
fit2$terms |> attr("term.labels") |> sort()
## [1] "age" "inc" "k5" "lwg" "wc"
fit3$terms |> attr("term.labels") |> sort()
## [1] "age" "inc" "k5" "lwg" "wc"
fit4$terms |> attr("term.labels") |> sort()
## [1] "age" "inc" "k5" "lwg" "wc"
fit5$terms |> attr("term.labels") |> sort()
## [1] "age" "inc" "k5" "lwg" "wc"
fit6$terms |> attr("term.labels") |> sort()
## [1] "age" "inc" "k5" "lwg" "wc"모두 동일한 모형임을 확인할 수 있다. 적합 내용을 확인해 보자.
summary(fit_1)
##
## Call:
## glm(formula = lfp ~ lwg + k5 + age + inc + wc, family = binomial,
## data = train_M)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.910361 0.607796 4.788 1.68e-06 ***
## lwg 0.646646 0.169648 3.812 0.000138 ***
## k5 -1.356904 0.220477 -6.154 7.54e-10 ***
## age -0.061678 0.012797 -4.820 1.44e-06 ***
## inc -0.030294 0.008737 -3.467 0.000526 ***
## wcyes 0.773789 0.224042 3.454 0.000553 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 824.47 on 602 degrees of freedom
## Residual deviance: 735.30 on 597 degrees of freedom
## AIC: 747.3
##
## Number of Fisher Scoring iterations: 4선택된 모형 fit_1에 대한 검진을 실시해 보자.
함수 residualPlots()으로 잔차 산점도 및 curvature test를 실시해 보자.
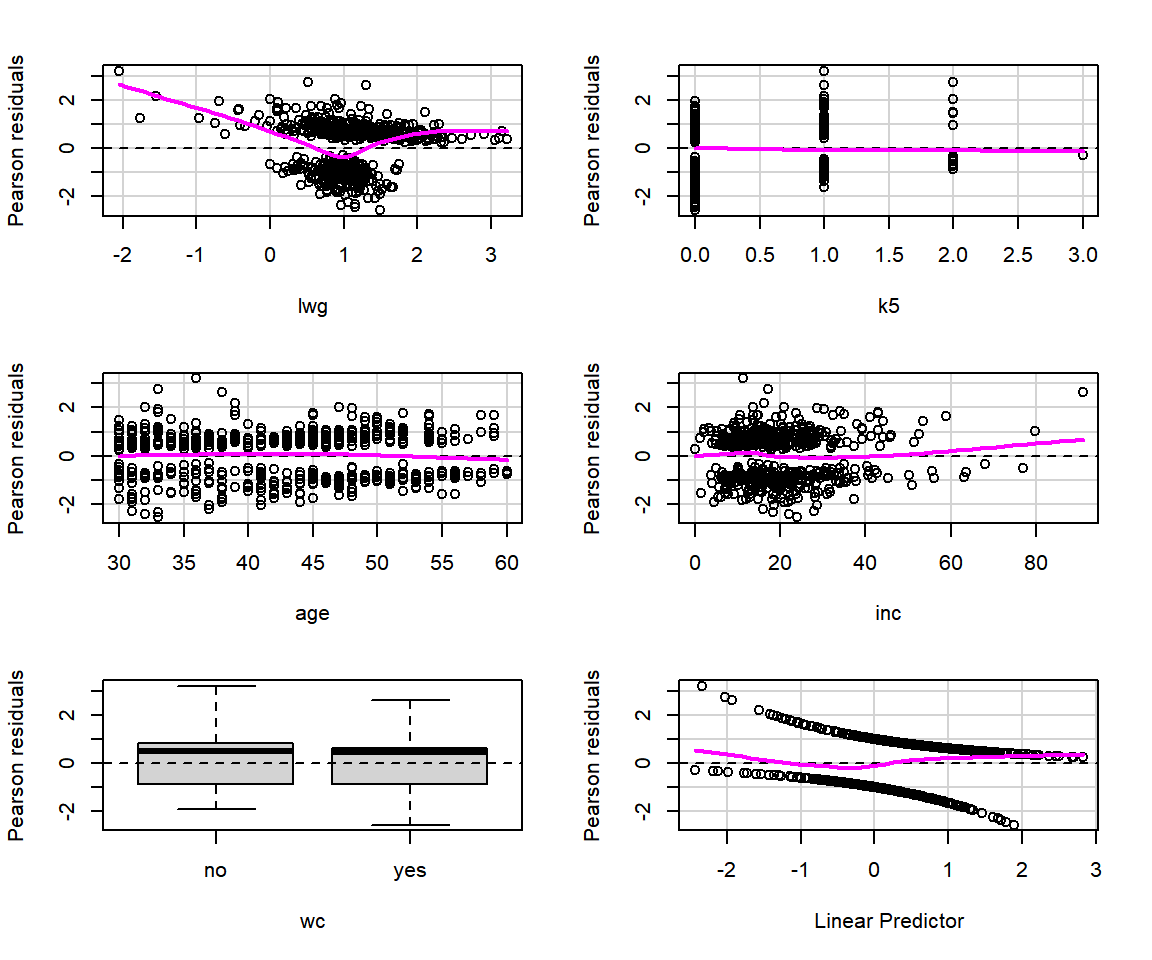
그림 2.14: 모형 fit_1의 잔차 산점도
## Test stat Pr(>|Test stat|)
## lwg 124.0900 < 2e-16 ***
## k5 0.0315 0.85908
## age 1.3815 0.23985
## inc 4.2999 0.03811 *
## wc
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1변수 lwg의 경우에는 2차항을 포함시키는 것이 필요한 것으로 보인다.
변수 inc의 경우에도 curvature test에서는 p-값이 0.05보다 작게 나왔으나, 잔차 산점도에서는 자료의 개수가 많지 않은 부분에서만 약간의 비선형 관계가 보이고 있는 것으로 나타나서, 변수 inc의 2차항은 포함시키지 않는 것으로 하겠다.
변수 lwg의 2차항을 포함한 모형을 적합시키고, 개별 회귀계수의 유의성을 95% 신뢰구간으로 확인해 보자.
fit_2 <- update(fit_1, . ~ . + I(lwg^2))
confint(fit_2)
## 2.5 % 97.5 %
## (Intercept) 4.62945865 8.12981369
## lwg -9.72717273 -5.14783290
## k5 -1.96295227 -0.95440249
## age -0.09877261 -0.04239908
## inc -0.05075725 -0.01139112
## wcyes -0.42920987 0.59066937
## I(lwg^2) 3.21738759 5.57124912변수 lwg의 2차항이 포함되면서 비유의적인 변수가 된 wc를 제외한 모형도 적합시키고 비교 대상으로 고려하자.
세 모형의 AIC와 BIC를 비교해 보자.
큰 차이가 있는 fit_1은 제외하고 나머지 두 모형의 분류성능을 비교해서 최종 모형을 선택하기로 하자.
Training data에 대한 두 모형의 예측을 실시해 보자.
모형 fit_2의 분류결과에 대한 평가 결과를 살펴보자.
\(d=0.5\) 를 분류 기준값으로 해서 함수 if_else()로 분류하고, 그 결과를 요인으로 전환하여 함수 confusionMatrix()에 적용시켜 보자.
train_M |>
mutate(lfp_hat = factor(if_else(pred_2 >= 0.5, "yes", "no"))) |>
with(confusionMatrix(data = lfp_hat, reference = lfp,
positive = "yes", mode = "everything"))
## Confusion Matrix and Statistics
##
## Reference
## Prediction no yes
## no 186 88
## yes 74 255
##
## Accuracy : 0.7313
## 95% CI : (0.6941, 0.7663)
## No Information Rate : 0.5688
## P-Value [Acc > NIR] : <2e-16
##
## Kappa : 0.4559
##
## Mcnemar's Test P-Value : 0.3071
##
## Sensitivity : 0.7434
## Specificity : 0.7154
## Pos Pred Value : 0.7751
## Neg Pred Value : 0.6788
## Precision : 0.7751
## Recall : 0.7434
## F1 : 0.7589
## Prevalence : 0.5688
## Detection Rate : 0.4229
## Detection Prevalence : 0.5456
## Balanced Accuracy : 0.7294
##
## 'Positive' Class : yes
## Confusion matrix와 정분류율, 민감도와 특이도 외에 많은 평가 측도의 값이 계산되어 있다.
다른 평가 측도의 자세한 설명은 함수 confusionMatrix()의 도움말에서 참고할 수 있다.
모형 fit_3의 분류결과에 대한 평가 결과도 확인해 보자.
함수 confusionMatrix()의 많은 결과 중 다음과 같이 원하는 결과만을 선택해서 출력할 수도 있다.
table_3 <- train_M |>
mutate(lfp_hat = factor(if_else(pred_3 >= 0.5, "yes", "no"))) |>
with(confusionMatrix(data = lfp_hat, reference = lfp,
positive = "yes", mode = "everything"))함수 confusionMatrix()의 결과가 할당된 객체 table_3의 요소 table에는 confusion matrix가 입력되어 있다.
정분류율 및 민감도, 특이도, F1 score 등은 다음과 같이 확인할 수 있다.
table_3$byClass[c("Sensitivity", "Specificity", "Precision", "F1")]
## Sensitivity Specificity Precision F1
## 0.7492711 0.7153846 0.7764350 0.7626113이번에는 두 모형의 ROC curve를 작성해서 비교해 보자.
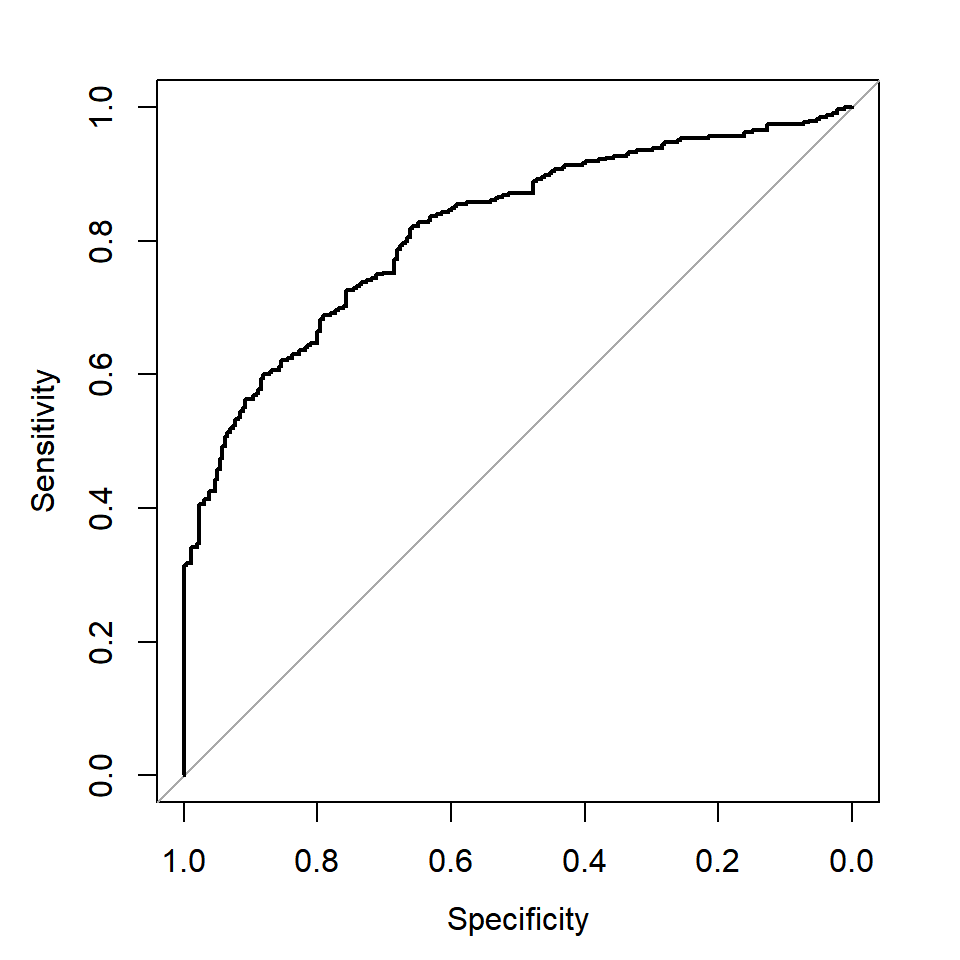
그림 2.15: 모형 fit_2의 ROC curve
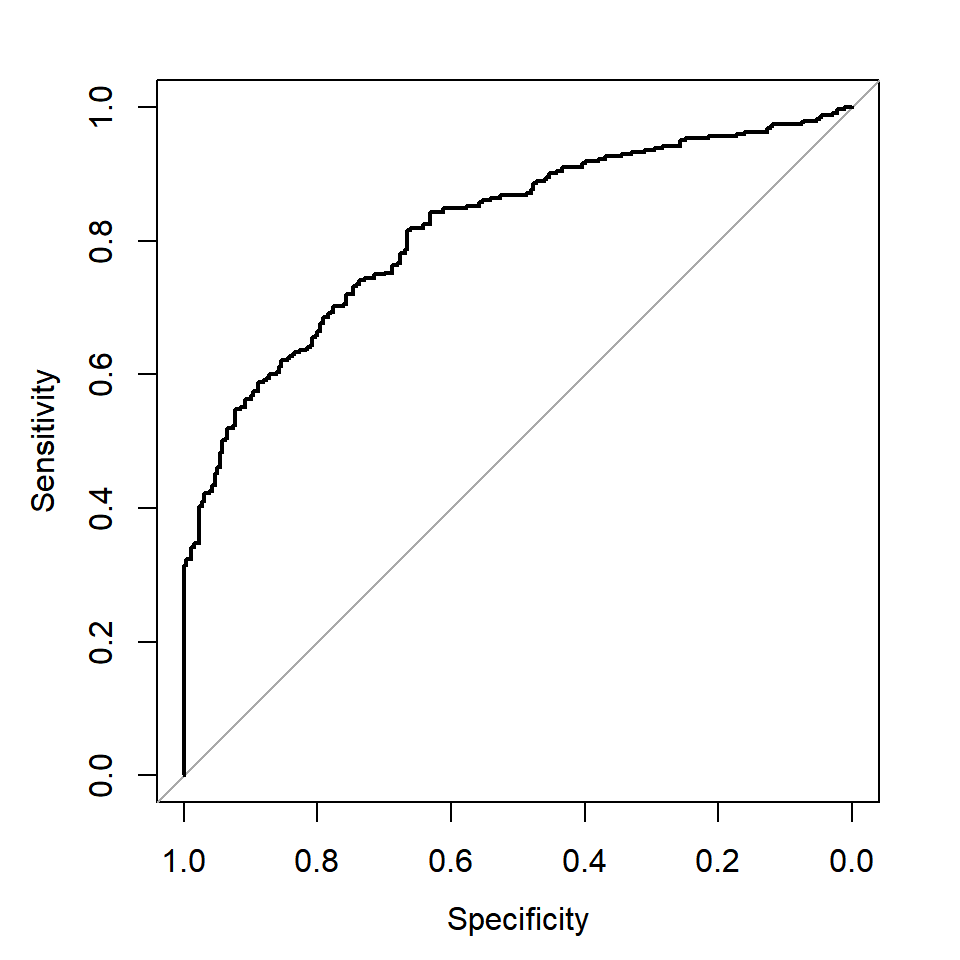
그림 2.16: 모형 fit_3의 ROC curve
AUC만 비교하고자 하는 경우에는 함수 auc()에 roc()의 결과를 입력하면 된다.
두 모형의 분류성능에는 큰 차이가 없으나,
AIC와 BIC, F1 score 등이 미세하게 좋은 fit_3를 최종 모형으로 선택하기로 하자.
fit_final <- fit_3
summary(fit_final)
##
## Call:
## glm(formula = lfp ~ lwg + k5 + age + inc + I(lwg^2), family = binomial,
## data = train_M)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 6.332365 0.891016 7.107 1.19e-12 ***
## lwg -7.339345 1.160271 -6.326 2.52e-10 ***
## k5 -1.440585 0.256668 -5.613 1.99e-08 ***
## age -0.070322 0.014343 -4.903 9.44e-07 ***
## inc -0.029801 0.009723 -3.065 0.00218 **
## I(lwg^2) 4.357318 0.590937 7.374 1.66e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 824.47 on 602 degrees of freedom
## Residual deviance: 611.31 on 597 degrees of freedom
## AIC: 623.31
##
## Number of Fisher Scoring iterations: 7최종 모형 fit_final을 사용하여 test data를 대상으로 분류를 시행하고, 그 결과에 대한 평가를 실시해 보자.
table_fc <- test_M |>
mutate(lfp_hat = factor(if_else(fc >= 0.5, "yes", "no"))) |>
with(confusionMatrix(data = lfp_hat, reference = lfp,
positive = "yes", mode = "everything"))table_fc$byClass[c(1,2,5,7)]
## Sensitivity Specificity Precision F1
## 0.6823529 0.7846154 0.8055556 0.7388535Training data에 대한 분류 결과와 비교해 보면 AUC와 특이도, Precision는 오히려 더 좋은 결과를 보이고 있음을 알 수 있다.
2.6 희귀사건의 분류
이항반응변수의 두 범주 중 “성공” 범주는 우리가 관심을 갖고 있는 Event 범주이다. 대부분의 경우에 Event 범주와 NonEvent 범주의 발생 가능성이 서로 큰 차이가 나지 않는 자료를 대상으로 분석을 진행하게 된다. 하지만 Event 범주의 발생 가능성이 구조적으로 매우 낮을 밖에 없는 상황도 있다. 예를 들면, 어떤 특정 의약품의 부작용 발생, 온라인 광고에 대한 클릭, 그리고 카드의 부정 사용 등은 발생할 가능성은 상대적으로 매우 낮지만 상당히 중요한 사건이라 하겠다.
이와 같이 “성공” 범주가 발생할 가능성이 매우 낮은 희귀사건인 경우에는 통계적 분류모형의 활용도에 큰 문제가 생길 수 있다. 즉, 통계모형에서 Event 범주에 대한 확률이 매우 낮게 추정될 가능성이 있고, 따라서 거의 모든 자료를 NonEvent로 분류하게 되어서 민감도가 너무 낮아지게 되는 것이다. 이렇게 되면 희귀사건을 제대로 분류하지 못하는 쓸모 없는 모형이 된다.
희귀사건의 영향력을 낮출 수 있는 대안으로는 분류기준값을 변경하는 방법과 training data에 대한 sampling 방식을 변경하는 방법이 있다.
분류기준값을 변경하는 방법은 민감도와 특이도의 trade-off를 고려해서 선정한 최적의 분류기준값으로 민감도를 높이는 방법이며, 로지스틱 회귀모형의 적합 과정 자체에는 어떠한 영향도 미치지 않는다. 분류기준값은 일반적으로 \(d=0.5\) 를 사용하는데, 0.5보다 더 작은 값을 사용하면 민감도를 높일 수 있다.
희귀사건에 대한 분류 성능이 떨어지는 이유는 training data에 Event 범주에 대한 정보가 부족하기 때문이다. 따라서 training data에서 Event 범주와 NonEvent 범주에 대한 정보량을 동일하게 만들어 줄 수 있다면, 희귀사건에 대한 분류 성능을 높일 수 있을 것이다. 두 범주의 정보량을 동일하게 만드는 방법은 다음과 같다.
Up-sampling : Event 범주 자료를 복원추출하여 case 확대
Down-sampling : NonEvent 범주 자료를 삭제하여 case 축소
SMOTE(Synthetic Minority Oversampling TEchnique) : Event 범주의 자료를 기존 자료의 선형결합으로 생성하여 case 확대. 설명변수가 모두 숫자형 변수인 경우에 적용.
예제를 가지고 구체적인 방법을 살펴보도록 하자.
\(\bullet\) 예제: ISLR::Caravan
패키지 ISLR의 Caravan은 어떤 보험 회사의 고객 5822명에 대한 자료이다.
86개 변수가 있으며, 마지막 변수인 Purchase는 고객의 캐러밴 보험 가입 여부를 나타낸 요인이다.
data(Caravan, package = "ISLR")
Caravan |>
count(Purchase) |>
mutate(p = n/sum(n))
## Purchase n p
## 1 No 5474 0.94022673
## 2 Yes 348 0.05977327캐러밴 보험에는 단 6%의 고객만이 가입한 상태이다. 분석 목적은 캐러밴 보험에 가입할 가능성이 높은 고객을 식별하는 것이다. 분석의 첫 단계로서 자료 분리를 진행하자.
set.seed(123)
x.id <- createDataPartition(Caravan$Purchase, p = 0.7, list = FALSE)[,1]
train_C <- Caravan |> slice(x.id)
test_C <- Caravan |> slice(-x.id)워낙 규모가 크기 때문에 변수선택 과정에 상당히 많은 시간이 소요되는 자료이다. 예제의 목적이 희귀사건에 대한 대안 탐색이어서 변수선택 및 검진 단계는 생략하고 그냥 모든 설명변수를 포함한 모형을 예측모형으로 사용하도록 하자.
모형 fit으로 test data에 대한 예측 및 분류를 실시해 보자.
pred <- predict(fit, newdata = test_C, type = "response")
yhat <- factor(if_else(pred >= 0.5, "Yes","No"))
table <- confusionMatrix(reference = test_C$Purchase, data = yhat, positive = "Yes")분류성능 평가를 위한 결과를 출력해 보자.
table$byClass[c(1,2,5,7)]
## Sensitivity Specificity Precision F1
## 0.02884615 0.99390987 0.23076923 0.05128205모형 fit은 1746개의 test data 중 단지 13개만 “Yes” 범주로 분류하였고, 결과적으로 지나치게 낮은 민감도가 산출되었다.
분석의 목적이 보험에 가입할 가능성이 높은 고객을 식별해 내는 것인데, test data에서 실제 보험에 가입한 고객 중에 단 2.9%만 제대로 식별했다는 것은 분석 목적에 전혀 부합하지 못한 분류 결과이다.
민감도를 향상시키는 방법으로 먼저 SMOTE 방법을 적용해 보자.
SMOTE 방법이 적용된 training data의 생성은 함수 smotefamily::SMOTE()로 할 수 있다.
기본적인 사용법은 SMOTE(X, target, K = 5)인데,
X는 숫자형 설명변수의 데이터 프레임 또는 행렬이고, target은 반응변수 벡터,
그리고 K는 자료 생성을 위한 nearest neighbors의 개수를 지정하는 것이다.
set.seed(123)
library(smotefamily)
smote <- SMOTE(dplyr::select(train_C, -Purchase), train_C$Purchase)함수 SMOTE()로 생성된 객체 smote의 요소 중 smote$data에는 SMOTE 기법으로 생성된 자료가 데이터 프레임 형태로 입력되는데, 반응변수의 이름이 class로, 유형은 문자형으로 변경된다.
따라서 분석의 편리를 위해 반응변수의 이름을 원래의 이름으로 다시 변경하고, 유형도 요인으로 변경하자.
SMOTE 기법으로 생성된 training data를 사용하여 예측모형을 다시 적합해 보자.
모형 fit_s로 test data에 대한 예측 및 분류를 실시해 보자.
pred_s <- predict(fit_s, newdata = test_C, type = "response")
yhat_s <- factor(if_else(pred_s >= 0.5, "Yes","No"))
table_s <- confusionMatrix(reference = test_C$Purchase, data = yhat_s, positive = "Yes")분류성능 평가를 위한 결과를 출력해 보자.
table_s$byClass[c(1,2,5,7)]
## Sensitivity Specificity Precision F1
## 0.5480769 0.7442144 0.1194969 0.1962134모형 fit에 의한 결과와 비교하면 정분류율과 특이도를 제외한 다른 측도는 모두 향상되었고,
특히 민감도는 크게 향상된 것을 볼 수 있다.
이번에는 모형 fit을 대상으로 분류기준값을 변경하는 방법을 적용해 보자.
모형 fit의 민감도는 0.029에 불구하지만, 특이도는 0.994으로 상당히 높은 값이다.
지나칠 정도로 높은 특이도를 조금 희생하더라도 민감도를 대폭 향상시킬 수 있는 방안으로 (민감도+특이도)를 최대화할 수 있는 최적 분류기준값을 찾아서 적용하는 것을 생각해 볼 수 있다.
여기에서 조심해야 하는 것은 최적 분류 기준값을 찾는 작업을 training data나 test data를 대상으로 진행해서는 안 된다는 것이다.
Training data를 대상으로 진행하면 overfitting의 문제가 생길 수 있으며, test data를 대상으로는 모형에 대한 어떠한 튜닝 작업도 진행해서는 안 되기 때문이다.
따라서 기존의 test data를 validation data와 test data로 다시 분리하고, validation data를 대상으로 최적 분류 기준값을 찾아야 할 것이다.
test_C를 절반으로 분리해서 validation data valid_C와 test data test_C1으로 나누자.
set.seed(123)
x.id <- createDataPartition(test_C$Purchase, p = 0.5, list = FALSE)[,1]
valid_C <- test_C |> slice(x.id)
test_C1 <- test_C |> slice(-x.id)최적 분류 기준값을 찾기 위해 먼저 모형 fit을 사용하여 validation data를 대상으로 확률 예측을 실시한다.
최적 분류 기준값을 찾는 작업은 패키지 pROC의 함수 coords()으로 할 수 있다.
기본적인 사용법은 coords(roc, x = "best", transpose = TRUE)이다.
roc는 함수 roc()로 생성된 객체이고, x = "best"를 지정하면 (민감도+특이도)를 최대화하는 분류 기준값을 찾는다.
transpose는 결과의 출력 형태에 대한 것으로, TRUE를 지정하면 벡터 형태로 결과가 출력된다.
(민감도+특이도)를 최대화하는 최적 분류 기준값은 0.0768547로 구해졌고, validation data를 대상으로는 민감도가 0.5192308, 특이도는 0.7819732로 계산되었다.
이제 변경된 분류 기준값을 사용하여 test data를 대상으로 다시 분류 작업을 진행해 보자.
pred_t <- predict(fit, newdata = test_C1, type = "response")
yhat_t <- factor(if_else(pred_t >= thres[1], "Yes", "No"))
table_t <- confusionMatrix(reference = test_C1$Purchase, data = yhat_t, positive = "Yes")분류성능 평가를 위한 결과를 출력해 보자.
table_t$byClass[c(1,2,5,7)]
## Sensitivity Specificity Precision F1
## 0.5961538 0.7746650 0.1435185 0.2313433민감도가 크게 향상된 것을 볼 수 있다. 민감도가 특히 중요한 분석에서 시도할 수 있는 방법이다.