1 장 회귀모형

사회현상, 자연현상, 경영현상이나 경제현상 등을 측정한 변수들의 변동은 그 현상과 관련된 여러 변수들과 관련이 있다고 볼 수 있다. 어떤 현상을 과학적 시각으로 설명하기 위해서는 해당 현상과 관련이 있는 변수들 사이의 관계를 설명하기 위한 적절한 모형을 설정해야 할 것이다. 회귀분석(regression analysis)이란 특정 현상과 그 현상에 영향을 주거나 혹은 관련이 있는 변수들 사이의 관계를 분석하고 모형화하기 위한 통계적 기법이다. 회귀분석에서는 변수들 사이의 함수관계를 이론적 근거나 경험적 판단에 의해서 설정하고, 관측된 자료에 의해서 함수관계를 추정해서 변수들 사이의 관계를 설명하거나 예측하는데 사용된다. 따라서 회귀분석은 사회과학, 공학, 물리학, 생물학, 경영학, 경제학, 의학 등 거의 모든 학문 분야에서 가장 널리 사용되고 있는 통계적 분석 방법인 것이다.

회귀모형을 설정할 때 우리가 관심이 있는 특정 현상의 변동을 나타내는 변수를 종속변수(dependent variable) 혹은 반응변수(response variable) 또는 결과변수(outcome variable)라고 하며, 일반적으로 \(Y\)로 표시한다. 반응변수가 나타내는 특정 현상에 연관되어 있을 것으로 판단되는 변수를 독립변수(independent variable) 혹은 설명변수(explanatory variable) 또는 예측변수(predictor variable)라고 하고, 일반적으로 \(X\)로 표시한다. 만일 설명변수의 수가 \(k\)개 있다고 하면 \(X_{1}, X_{2}, \ldots, X_{k}\)로 표시한다.

예를 들어, 회사 마케팅 부서에서 특정 제품의 매출액 변동을 예측할 수 있는 모형을 설정하고자 할 때 제품의 매출액 변동에 영향을 줄 수 있는 변수들로 광고비 지출액, 가격수준, 기술수준, 디자인 선호수준, 소득수준, 영엽사원의 수, 경쟁제품의 수 등을 생각할 수 있는데, 이 경우에 반응변수는 제품의 매출액이 되고, 광고비 지출액 등 나머지 변수들은 설명변수가 된다.

또 다른 예로써 투자자문회사에서 고객의 투자행위에 대한 예측모형을 개발할 때 투자행위에 영향을 미칠 수 있는 변수들로 연소득 수준, 미래 경제상황지수, 시장 이자율 등을 이용하게 되는데, 여기에서 반응변수는 고개들의 투자액이 되고, 연소득 수준 등은 설명변수가 된다.

회귀모형은 모형에 포힘되는 설명변수가 한 개인 경우에는 단순회귀모형(simple regression model)이라고 하고, 두 개 이상의 설명변수가 모형에 포함되는 경우에는 다중회귀모형(multiple regression model)이라고 한다.

1.1 반응변수와 설명변수 사이의 관계 설정

반응변수와 설명변수 사이의 관계는 일반적으로 결정적 관계(deterministic relation)와 확률적 관계(stochastic relation)로 구분해 볼 수 있다. 결정적 관계는 반응변수와 설명변수 사이에 정확한 수학적 함수관계가 성립되는 경우를 의미하는 것으로 \(Y=f(X)\)와 같이 표시할 수 있다. 여기에서 함수 \(f\) 는 직선, 곡선 혹은 더 복잡한 형태의 함수식이 될 수 있다. 결정적 관계에서는 설명변수의 값이 주어지면, 함수 \(f\) 에 의하여 대응되는 반응변수의 값이 유일하게 결정된다. 예를 들어, 제품의 판매단가가 2만원 일 때 판매개수(\(X\))와 매출액(\(Y\)) 사이의 관계는 \(Y=2X\)로 표현되는 결정적 관계가 성립한다. 반응변수와 설명변수의 관계가 결정적인 경우에 함수 \(f\) 에 대한 추정은 통계적 접근이 필요하지 않는 분야가 된다.

확률적 관계는 설명변수로 반응변수의 변동을 100% 설명할 수 없는 관계를 의미한다. 예를 들어, 특정 제품의 매출액(\(Y\))과 광고비 지출액(\(X\)) 사이의 관계를 생각해 보자. 일반적으로 광고비 지출을 증가시키면 매출액이 증가하겠지만, 광고비 지출액만으로 매출액의 변동을 100% 설명하는 것은 불가능하다. 가격수준, 기술수준, 디자인 선호수준, 소득수준 등 매출액의 변동에 영향을 줄 수 있는 다른 많은 변수를 포함시키더라도 매출액 변동을 100% 설명하는 것은 불가능하다고 할 수 있다.

이와 같이 설명할 수 없는 반응변수의 변동이 항상 존재하는 경우에는 반응변수와 설명변수의 관계를 다음과 같이 오차항 \(\varepsilon\) 을 포함시켜서 표현할 수 있다.

\[\begin{equation} Y = f(X) + \varepsilon \tag{1.1} \end{equation}\]

식 (1.1)에서 함수 \(f(X)\) 는 반응변수와 설명변수 사이에 존재하는 체계적 정보(systematic information)를 표현하며, 오차항 \(\varepsilon\)는 함수 \(f(X)\) 로 설명되지 않는 반응변수의 변동을 나타내는 확률변수로서 평균은 \(0\) 이며, 설명변수와는 독립이라고 가정한다.

1.2 회귀분석의 목적

회귀분석의 목적은 식 (1.1)의 함수 \(f\) 의 추정이라고 할 수 있는데, 함수 \(f\) 를 추정하려는 이유는 수집된 데이터에 존재하는 반응변수와 설명변수 사이의 관계를 명확하게 설명하려는 ’자료의 기술’과 새롭게 주어진 설명변수의 값에 대응되는 반응변수의 값에 대한 ’예측’이라고 할 수 있다.

자료의 기술(Data description)

자료들의 특징이나 변수들 사이의 관계 등을 명확하게 밝히는 것이 분석 목적이 되는 경우가 있다. 이런 경우에는 두 변수 사이의 함수형태를 가정하지 않는 비모수적 회귀모형이 효과적인 분석 방식이 될 수 있다. 그림 1.1는 2014년 호주 빅토리아 주에서 측정된 일일 최고 기온과 전기 사용량의 산점도와 두 변수에 대한 비모수적 회귀모형의 적합 결과를 나타낸 그래프이다. 명확한 2차 곡선의 관계가 잘 드러난 예제이다.

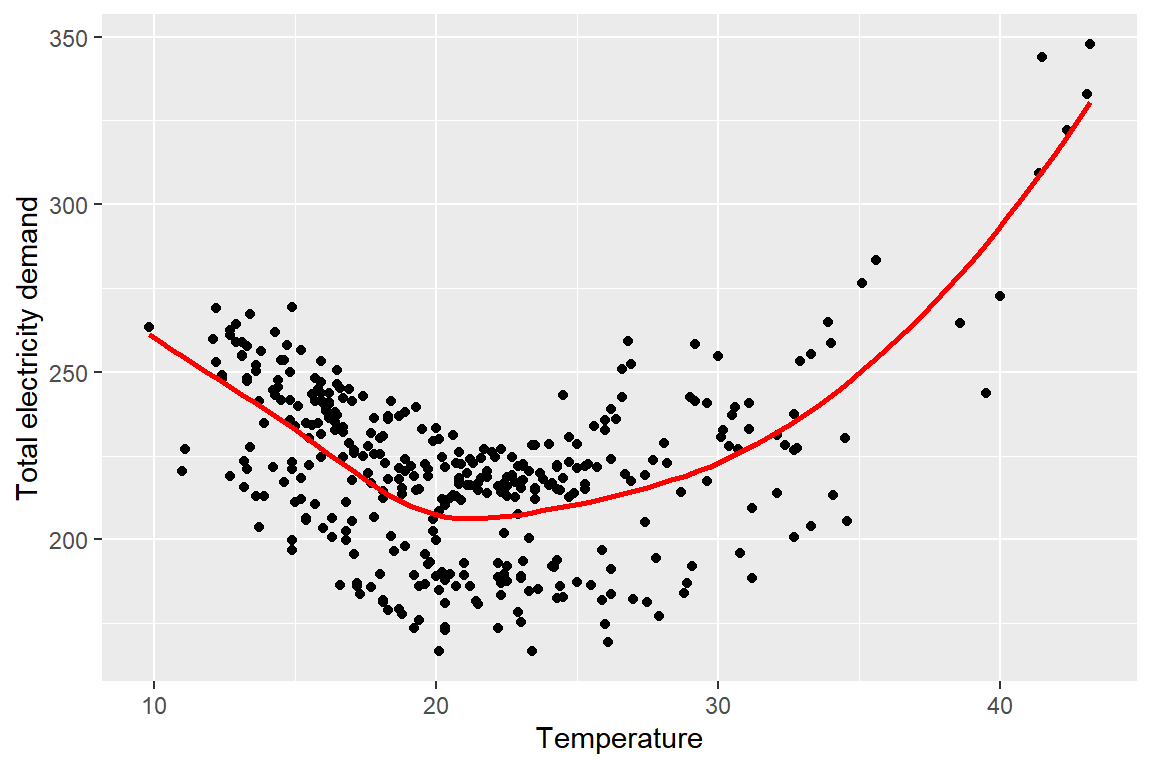
그림 1.1: 자료의 기술 목적으로 사용된 회귀모형의 예

예측(Prediction)

새롭게 관측되는 변수 \(X\) 의 자료에 대응되는 변수 \(Y\) 의 가장 정확한 예측값을 생성하는 것이 분석의 목적이 되는 경우가 많이 있다. 식 (1.1)의 관계에서 변수 \(Y\) 의 예측값 \(\widehat{Y}\) 은 다음과 같이 생성된다.

\[\begin{equation} \widehat{Y} = \hat{f}(X) \end{equation}\]

변수 \(Y\) 는 함수 \(f\) 와 오차항 \(\varepsilon\) 의 합으로 구성되어 있지만, 우리가 예측할 수 있는 대상은 두 변수 사이의 체계적 정보를 담고 있는 함수 \(f\) 뿐이다. 오차항은 변수 \(Y\) 에서 함수 \(f\) 로 설명되지 않는 변동을 나타내는 것으로서 확률적 관계에서는 항상 존재하며, 예측이 가능한 대상은 아니다.

예측의 정확도는 변수 \(Y\) 와 예측값 \(\widehat{Y}\) 의 차이의 제곱에 대한 평균으로 표시될 수 있다.

\[\begin{align} E(Y-\widehat{Y})^{2} & = E\left(f(X)+\varepsilon - \hat{f}(X) \right)^{2} \\ & = \left(f(X)-\hat{f}(X) \right)^{2} + Var(\varepsilon) \tag{1.2} \end{align}\]

식 (1.2)에서 \(Var(\varepsilon)\) 은 변수 \(Y\) 의 고유 특성으로 발생되는 변동이기 때문에 분석자가 감소시킬 수 있는 변량은 아니다. 예측의 정확도를 높이기 위해 분석자가 줄일 수 있는 변량은 \(\left(f(X)-\hat{f}(X) \right)^{2}\) 이다.

1.3 회귀모형의 종류

1.3.1 모수적 회귀모형

모형 \(f(X)\)에 대해서 직선 혹은 곡선 등의 함수형태를 가정하는 방법이 있다. 이런 접근 방식을 모수적 회귀모형(parametric regression model)이라고 하며, 이 책에서 주로 살펴볼 모형이다.

반응변수와 설명변수의 관계가 설정된 함수형태를 항상 따른다는 것은 매우 강한 제약 조건이 될 수 있으나, 반응변수와 설명변수 사이에 존재하는 참 관계를 잘 나타낼 수 있다면 매우 효과적인 분석 모형이 될 것이다. 실제로 참 관계는 매우 복잡한 형태가 될 수 있으며, 대부분의 경우 정확한 모습은 미리 알 수 없다. 만일 참 관계가 그림 1.2와 같다면, 선형식으로 충분히 근사될 수 있을 것이다.

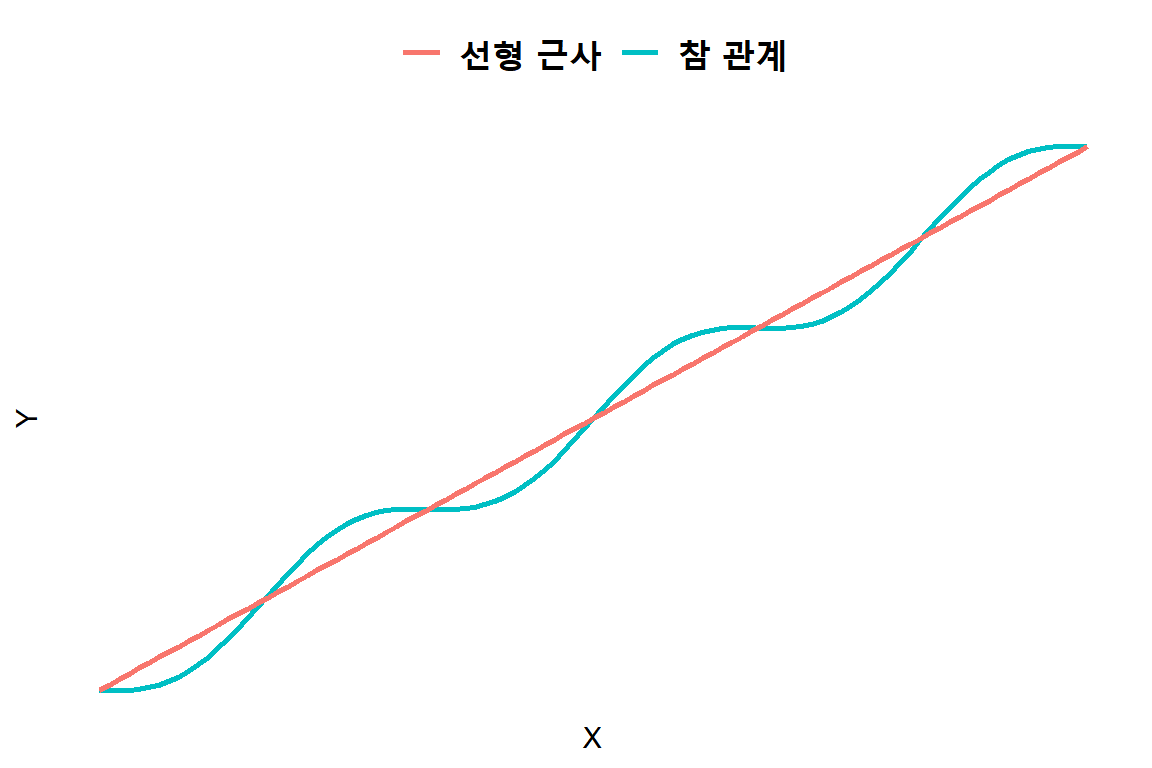
그림 1.2: 복잡한 관계에 대한 선형회귀 근사

단순선형회귀모형

예를 들어, 특정 제품의 매출액과 광고비 지출액의 관계가 그림 1.2와 같다고 하면, 두 변수의 관계는 다음과 같이 표현할 수 있다.

\[\begin{equation} Y = \beta_{0} + \beta_{1}X + \varepsilon \tag{1.3} \end{equation}\]

반응변수와 설명변수에 대한 회귀모형을 식 (1.3)와 같이 설정하면, 회귀직선은 두 변수 사이의 참 관계(true relation)에 대한 근사(approximation)를 의미한다. 식 (1.3)에서 \(\beta_{0}\) 와 \(\beta_{1}\) 은 두 변수의 관계를 규정하는 ’모집단 회귀직선’의 Y축 절편과 직선의 기울기를 각각 나타내는 있는 모수(parameter)이며, 회귀계수(regression coefficient)라고 불린다.

식 (1.3)를 단순선형회귀모형(simple linear regression model)이라고 부른다. 여기에서 ’단순’은 모형에 설명변수가 하나만 있다는 것을 의미하고, ’선형’은 모형에 포함된 모수 사이의 관계가 선형임을 의미한다.

단순회귀모형의 경우에 두 변수 사이의 관계를 탐색하기 위한 첫 번째 단계는 산점도를 작성하는 것이다. 예를 들어, 함수 \(f\) 를 추정하기 위해 두 변수에 대한 \(n=50\) 의 자료를 수집하여 작성한 산점도가 그림 1.3와 같다고 하자.

그림 1.3에서 자료들은 직선 위에 위치하지 않고 있는데, 이와 같은 반응변수의 관측값과 직선 (\(\beta_{0}+\beta_{1}X\))의 차이를 나타내기 위하여 오차항 \(\varepsilon\)이 포함되었다. 오차항은 광고비 지출 이외의 다른 변수들의 영향이나 측정 오차 등을 포함하는 통계적 오차가 된다.

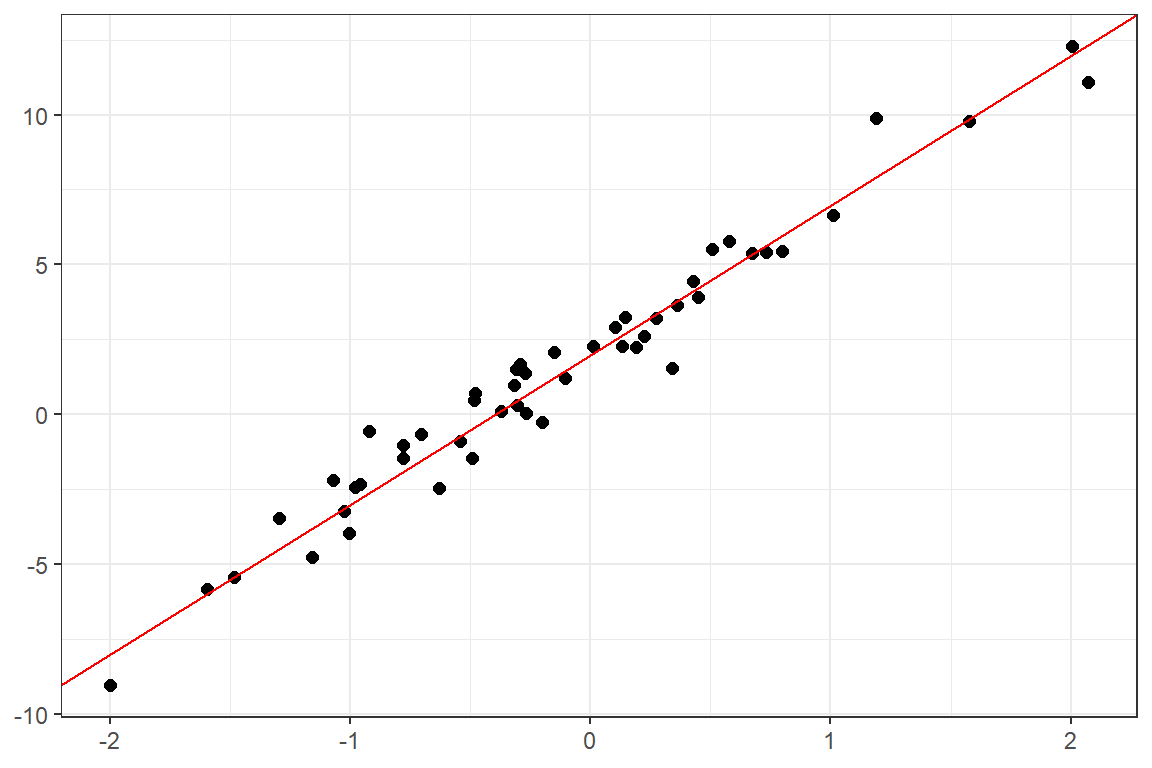
그림 1.3: 직선 관계 함수

함수 \(f\) 를 추정하는 데 사용되는 자료를 training data(학습 데이터)라고 한다. Training data의 산점도가 그림 1.3와 같다면 함수 \(f\)를 식 (1.3)에 주어진 직선 형태로 가정할 수 있을 것이다. 추정된 \(\hat{f}(x)\) 인 직선이 training data를 잘 설명하고 있음을 알 수 있다.

또한 만일 training data의 산점도가 그림 1.4와 같다면, \(f\) 를 2차 함수 형태로 가정할 수 있을 것이다. 추정된 \(\hat{f}(x)\) 인 2차 곡선이 training data를 잘 설명하고 있음을 알 수 있다.

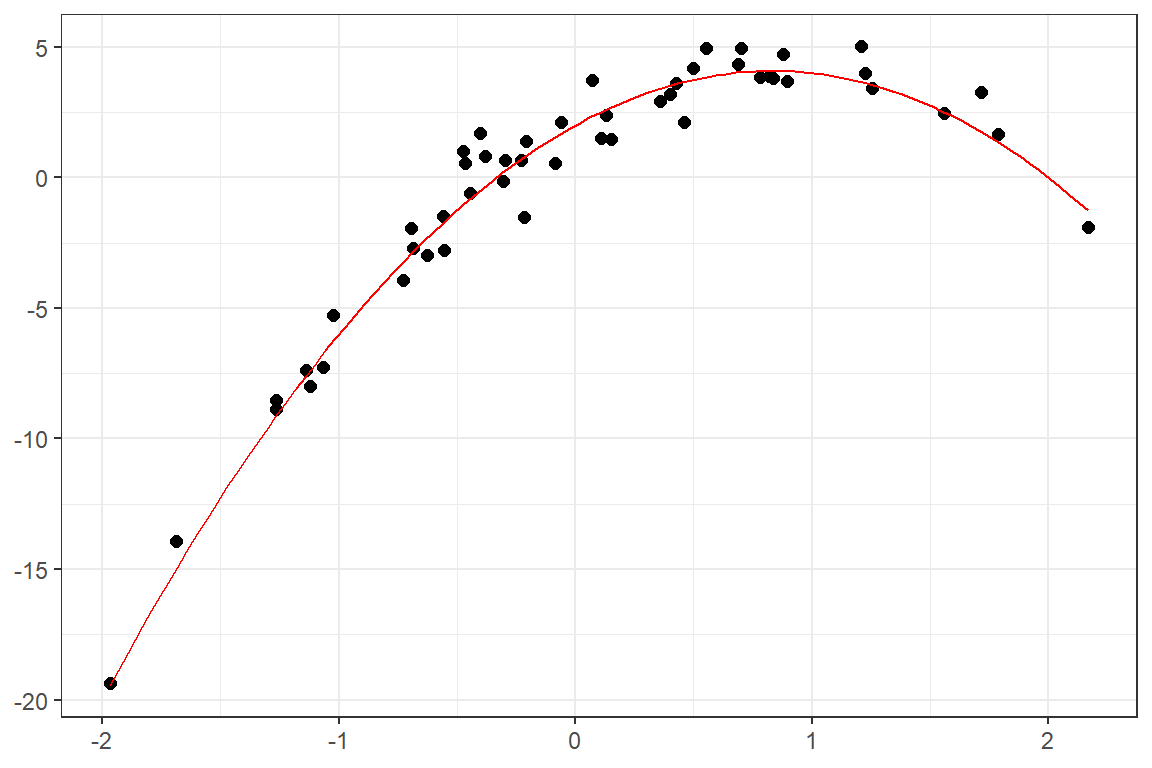
그림 1.4: 이차 관계 함수

회귀분석의 중요한 목적 중 하나는 회귀모형에 포함된 모수를 추정하는 것이다. 이러한 절차를 모형의 적합(fitting)이라고 하며, 2장에서는 회귀분석에서 가장 많이 사용되는 추정 방법인 최고제곱추정 방법이 소개될 것이다. 예를 들어 그림 1.3에 주어진 자료를 이용해서 구한 최소제곱추정에 의한 회귀직선식은 다음과 같이 주어진다.

\[\begin{equation} \hat{Y}=2.1 + 4.9X \end{equation}\]

여기에서 \(\hat{Y}\)은 광고비 지출액이 \(X\)일 때 대응되는 평균 매출액의 추정값이 된다.

일반적으로 추정된 회귀식은 설명변수가 관측된 범위 내에서만 적용하는 것이 바람직하다. 예를 들면, 그림 1.5에서 두 변수 \(Y\)와 \(X\)에 대한 자료가 \(x_{1} \leq X \leq x_{2}\)의 범위에서 수집되었다고 하자. 이 범위에서 참 관계는 직선으로 근사될 수 있을 것이다. 그러나 \(X \geq x_{2}\)의 범위에서 반응변수의 값을 선형 근사 관계를 근거로 예측하고자 한다면 심각한 신뢰성 문제가 발생하게 된다. 설명변수가 관측된 범위를 벗어난 구역에 대한 예측은 가능한 시도하지 않는 것이 좋겠지만, 시도를 해야만 하는 상황이라면 매우 조심해서 예측 결과를 적용해야 할 것이다.

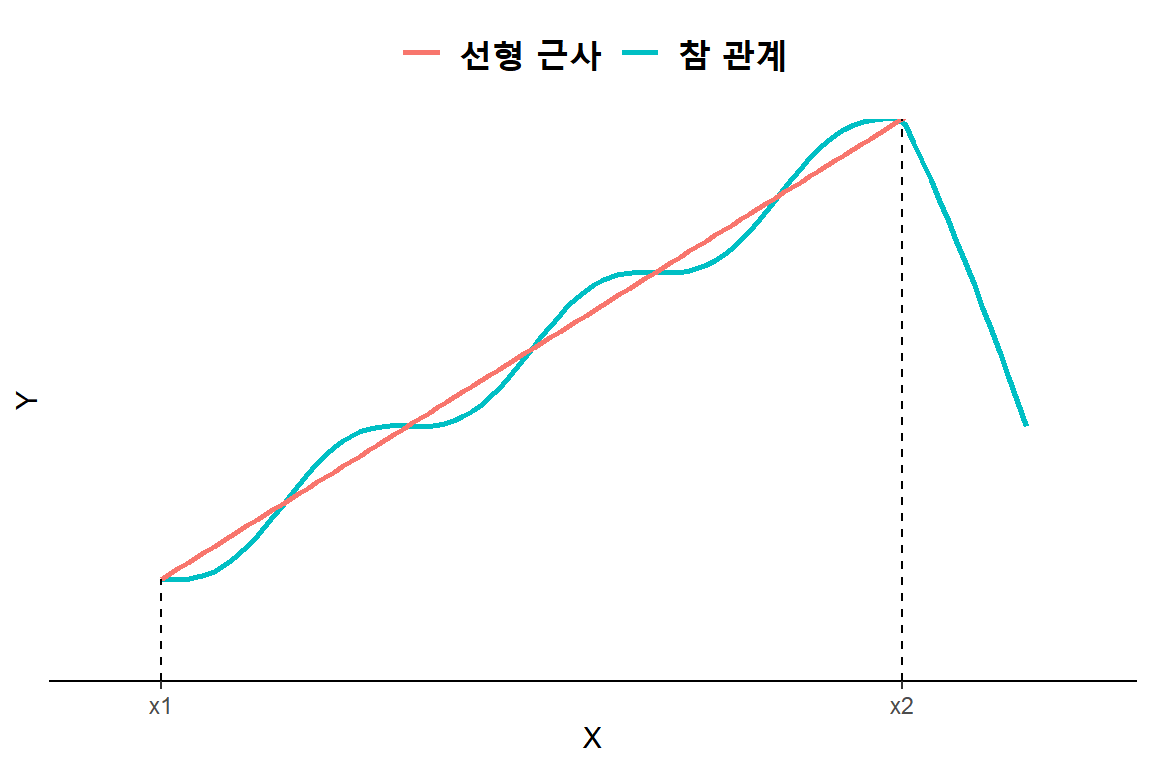
그림 1.5: 회귀모형의 유효성 문제

다중회귀모형

설명변수의 개수를 \(k\) 개로 늘린 회귀모형은 다음과 같이 설정할 수 있다.

\[\begin{equation} Y = \beta_{0} + \beta_{1}X_{1} + \cdots + \beta_{k}X_{k} + \varepsilon \tag{1.4} \end{equation}\]

식 (1.4)을 다중선형회귀모형(multiple linear regression model)이라고 부른다. 여기에서 ’다중’은 모형에 포함된 설명변수의 개수가 두 개 이상인 경우를 의미한다.

반응변수의 변동을 설명변수 하나만으로 충분히 설명한다는 것은 현실적으로 거의 불가능한 상황이라고 할 수 있다. 따라서 실제 상황에서는 설명변수의 개수를 \(k\) 개로 늘린 다중회귀모형이 더 현실적인 모형이라고 할 수 있다.

1.3.2 비모수적 회귀모형

모형 \(f(X)\)에 대해 특별한 함수 형태를 가정하지 않는 방법도 있다. 비모수적 회귀모형(non-parametric regression model)이라고 하는데, 자세한 설명은 이 책의 수준을 벗어나기 때문에 생략하겠지만, 자료탐색 수준에서 상당히 많이 사용되는 국소회귀(local regression)가 여기에 속하는 방법이다.

모수적 회귀모형에서는 회귀함수 \(f\)의 형태에 대한 가정을 하게 되는데, 만일 이 가정에 오류가 있다면 추정 및 예측 결과에도 문제가 있게 된다.

그림 1.6에서 볼 수 있는 산점도는 비교적 함수의 형태가 명확한 그림 1.3와 그림 1.4의 경우와는 많이 다른 경우가 된다.

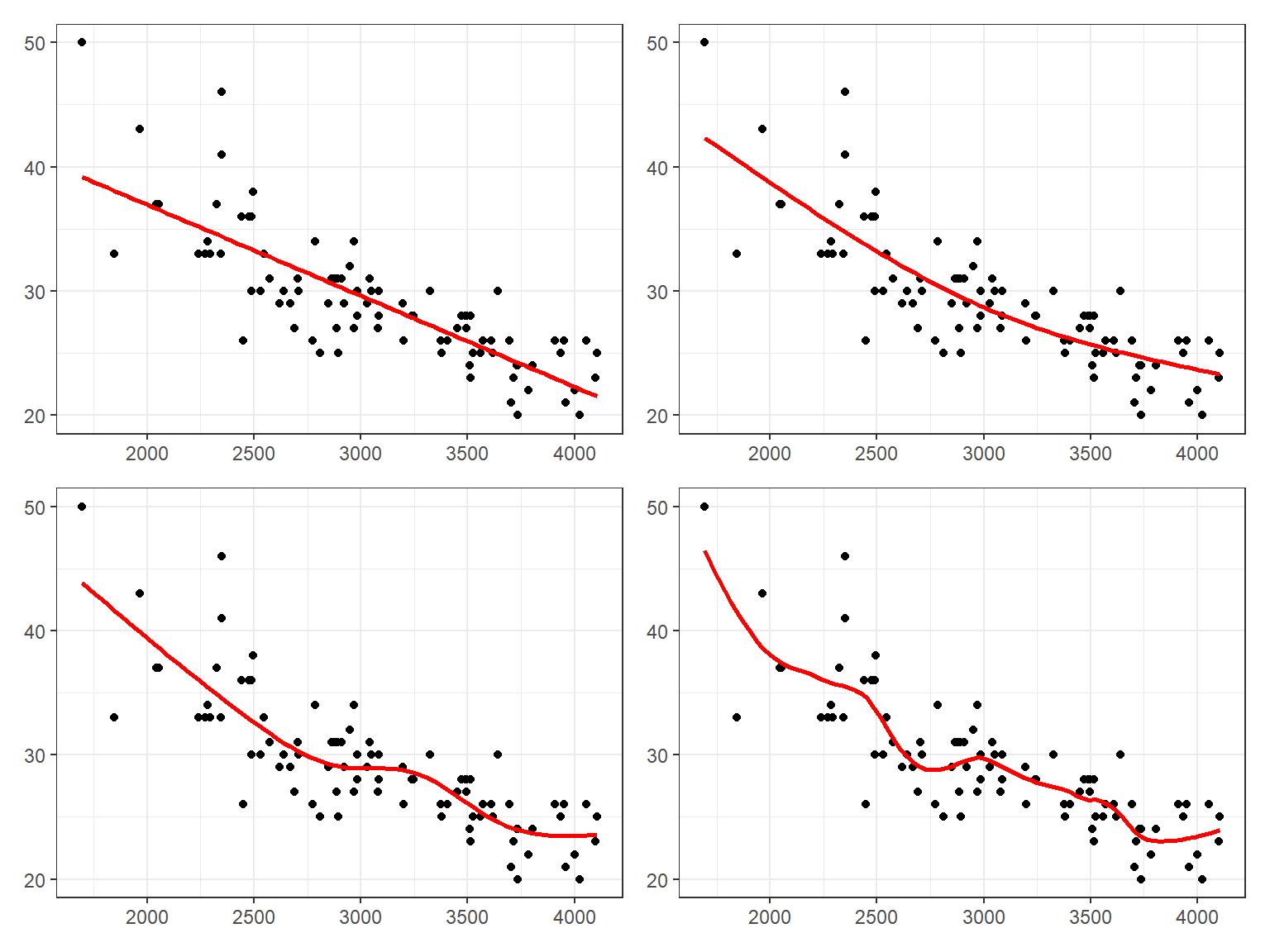
그림 1.6: 상대적으로 복잡한 형태의 관계

위쪽에 있는 두 그래프는 모두 모수적 회귀모형을 사용해서 함수 \(f\) 를 추정한 결과를 나타내고 있다. 왼쪽 위 그래프는 두 변수의 관계를 직선으로 가정하고 추정한 직선이 표시되어 있고, 오른쪽 위 그래프는 두 변수의 관계를 2차 곡선으로 가정하고 추정한 곡선이 표시되어 있다. 하지만 두 그래프에서 보여준 추정 결과는 모두 만족스럽지 못하다고 하겠다.

아래쪽에 있는 두 그래프는 비모수 회귀모형에 속한 두 모형으로 추정된 곡선이 표시되어 있다. 주어진 자료에 대해 비교적 잘 설명하고 있음을 알 수 있다.

주어진 자료를 잘 설명할 수 있다는 장점은 있지만, 비모수적 회귀모형으로 함수 \(f\) 를 효과적으로 추정하기 위해서는 많은 자료가 필요하다는 문제가 있다. 특히 다중회귀모형의 경우에는 모수적 회귀모형에 비해 대단히 많은 자료가 필요하기 때문에, 현실적으로 적용하는 데 한계가 있을 수 있다.

1.4 R의 역할

최종 회귀모형을 얻기 위해서는 많은 분석 단계를 거쳐야 한다. 자료의 특성을 잘 보여줄 수 있는 그래프 작성이 가능해야 하며, 반복적인 처리를 통해서 적합 과정의 문제를 발견할 수 있어야 하고, 효과적인 예측을 실시할 수 있어야 한다. 따라서 성공적인 분석을 실시하기 위해서는 고급통계분석에 가장 적절한 프로그래밍 언어를 선택해야 한다.

이 책에서는 R을 사용하여 회귀분석의 모든 과정을 자세하게 소개할 것이다. 기본적인 R 사용법이나 패키지 dplyr과 ggplot2에 대해서는 책을 읽는 분들이 어느 정도 익숙하다는 가정을 하고 있다. 또한 책에 제공된 R code에는 프롬프트(> 또는 +)를 제거하였고, console 창에 출력되는 결과물은 ##으로 시작되도록 하였다.

이 책을 작성할 때의 R 세션 정보는 다음과 같다.

sessionInfo()
## R version 4.4.0 (2024-04-24 ucrt)
## Platform: x86_64-w64-mingw32/x64
## Running under: Windows 11 x64 (build 22631)
## 
## Matrix products: default
## 
## 
## locale:
## [1] LC_COLLATE=Korean_Korea.utf8  LC_CTYPE=Korean_Korea.utf8   
## [3] LC_MONETARY=Korean_Korea.utf8 LC_NUMERIC=C                 
## [5] LC_TIME=Korean_Korea.utf8    
## 
## time zone: Asia/Seoul
## tzcode source: internal
## 
## attached base packages:
## [1] splines   stats     graphics  grDevices utils     datasets  methods  
## [8] base     
## 
## other attached packages:
##  [1] patchwork_1.2.0 expsmooth_2.3   fma_2.5         forecast_8.22.0
##  [5] fpp2_2.5        lubridate_1.9.3 forcats_1.0.0   stringr_1.5.1  
##  [9] dplyr_1.1.4     purrr_1.0.2     readr_2.1.5     tidyr_1.3.1    
## [13] tibble_3.2.1    ggplot2_3.5.1   tidyverse_2.0.0
## 
## loaded via a namespace (and not attached):
##  [1] gtable_0.3.5      xfun_0.44         bslib_0.7.0       lattice_0.22-6   
##  [5] tzdb_0.4.0        quadprog_1.5-8    vctrs_0.6.5       tools_4.4.0      
##  [9] generics_0.1.3    curl_5.2.1        parallel_4.4.0    fansi_1.0.6      
## [13] highr_0.10        xts_0.13.2        pkgconfig_2.0.3   Matrix_1.7-0     
## [17] lifecycle_1.0.4   farver_2.1.2      compiler_4.4.0    munsell_0.5.1    
## [21] htmltools_0.5.8.1 sass_0.4.9        yaml_2.3.8        pillar_1.9.0     
## [25] crayon_1.5.2      jquerylib_0.1.4   cachem_1.0.8      nlme_3.1-164     
## [29] fracdiff_1.5-3    tidyselect_1.2.1  digest_0.6.35     stringi_1.8.4    
## [33] bookdown_0.39     labeling_0.4.3    tseries_0.10-56   fastmap_1.1.1    
## [37] grid_4.4.0        colorspace_2.1-0  cli_3.6.2         magrittr_2.0.3   
## [41] utf8_1.2.4        withr_3.0.0       scales_1.3.0      timechange_0.3.0 
## [45] TTR_0.24.4        rmarkdown_2.26    quantmod_0.4.26   nnet_7.3-19      
## [49] timeDate_4032.109 zoo_1.8-12        hms_1.1.3         urca_1.3-3       
## [53] evaluate_0.23     knitr_1.46        lmtest_0.9-40     mgcv_1.9-1       
## [57] rlang_1.1.3       Rcpp_1.0.12       glue_1.7.0        rstudioapi_0.16.0
## [61] jsonlite_1.8.8    R6_2.5.1