2 장 단순선형회귀모형
선형회귀모형의 가장 기본적인 형태는 한 개의 설명변수로 반응변수의 변동을 설명하려는 단순회귀모형이다. 이 장에서는 특히 두 변수의 관계가 직선인 경우에 대해서만 살펴보겠다.
2.1 단순회귀모형의 설정
설명변수가 하나이고, 반응변수와의 관계가 직선인 경우에 회귀모형은 다음과 같이 설정된다.
\[\begin{equation} Y_{i} = \beta_{0} + \beta_{1}X_{i} + \varepsilon_{i}, ~~i=1,2,\ldots,n \tag{2.1} \end{equation}\]
여기에서 \(Y_{i}\) 는 반응변수의 \(i\) 번째 값, \(X_{i}\) 는 설명변수의 \(i\) 번째 값을 표시한다. 절편 \(\beta_{0}\) 와 \(\beta_{1}\) 은 모수(parameter)이며, 따라서 알려지지 않은 상수(constant)이다. 오차항 \(\varepsilon_{i}\) 는 반응변수의 변동 중 설명변수로 설명할 수 없는 부분을 나타내는 확률변수인데, \(n\) 개의 오차항이 모두 평균이 0, 분산은 \(\sigma^{2}\) 이며, 서로 독립이라고 가정한다. 또한 설명변수의 값 \(X_{i}\) 는 분석자에 의해서 값이 통제될 수 있는 변량으로써 확률변수가 아닌 상수라고 가정한다.
이러한 가정에서 단순회귀모형의 반응변수 \(Y_{i}\) 의 특성을 다음과 같이 유도할 수 있다.
\(Y_{i}\) 는 상수인 \(\beta_{0}+\beta_{1}X_{i}\)와 확률변수인 \(\varepsilon_{i}\)의 합으로 구성되어 있다. 따라서 \(Y_{i}\)는 확률변수이다.
설명변수의 값이 \(X_{i}\)로 주어졌을 때, 확률변수 \(Y_{i}\)의 평균은 다음과 같다.
위 수식에서 \(\beta_{0}+\beta_{1}X_{i}\)는 상수이기 때문에 기대값은 동일한 값이 되고, \(E(\varepsilon_{i})=0\) 은 가정에 의한 결과이다.
- 설명변수의 값이 \(X_{i}\)로 주어졌을 때, 확률변수 \(Y_{i}\)의 분산은 다음과 같다.
위 수식에서 \(\beta_{0}+\beta_{1}X_{i}\)는 상수이기 때문에 분산은 0이고 되고, \(Var(\varepsilon_{i}) = \sigma^{2}\) 는 가정에 의한 결과이다.
위 결과를 종합하면 설명변수의 값이 \(X_{i}\)로 주어졌을 때, 확률변수 \(Y_{i}\)는 평균이 \(\beta_{0}+\beta_{1}X_{i}\)이고 분산이 \(\sigma^{2}\)이 된다. 즉, 반응변수의 평균은 설명변수의 값에 따라 절편이 \(\beta_{0}\)이고 기울기가 \(\beta_{1}\)인 직선을 따라 움직인다는 것을 알 수 있는데, 이 직선을 ’모집단 회귀직선’이라고 한다. 또한 반응변수의 평균은 설명변수의 값에 따라 변하지만, 분산은 항상 일정한 값을 갖는다는 것을 알 수 있다.
\(n\)개의 오차항 \(\varepsilon_{1}, \ldots, \varepsilon_{n}\)들이 서로 독립이라고 가정했기 때문에 반응변수도 서로 독립이 된다. 따라서 \(Y_{i}\)와 \(Y_{j}\)는 \(i \ne j\) 라면, 서로 독립이기 때문에 두 변수의 공분산은 \(Cov(Y_{i}, Y_{j})=0\) 이 된다.
두 확률변수 \(X\)와 \(Y\)의 공분산 \(Cov(X,Y)\)는 다음과 같이 정의된다.
\[\begin{align} Cov(X,Y) & = E\left((X-E(X))(Y-E(Y)) \right) \\ & = E(XY) - E(X)E(Y) \tag{2.2} \end{align}\]
만일 확률변수 \(X\)와 \(Y\)가 서로 독립이면, \(E(XY)=E(X)E(Y)\)의 관계가 성립한다. 따라서 서로 독립인 두 확률변수의 공분산은 식 (2.2)에 의해서 0이 됨을 알 수 있다.
공분산 \(Cov(X,Y)\) 는 변수 \(X\)와 \(Y\) 사이에 존재하는 선형 관련성을 표현하고 있다. 식 (2.2)에서 볼 수 있듯이 공분산은 변수 \((X-E(X))(Y-E(Y)\)의 평균값을 나타낸다. 만일 \((X,Y)\)의 자료 중 \((X-E(X))>0\) 이고 \((Y-E(Y))>0\) 을 만족하거나 \((X-E(X))<0\) 이고 \((Y-E(Y))<0\) 인 조건을 만족하는 자료가 많게 되면 변수 \((X-E(X))(Y-E(Y)\) 의 값은 대부분 양수의 값이 되며, 따라서 변수 \((X-E(X))(Y-E(Y)\) 의 평균값인 두 변수의 공분산은 0보다 큰 값을 갖게 된다. 하지만 \((X,Y)\)의 자료 중 \((X-E(X))\)와 \((Y-E(Y))\)의 부호가 서로 반대가 되는 자료가 많게 되면 변수 \((X-E(X))(Y-E(Y)\)의 값은 대부분 음수의 값이 되며, 따라서 변수 \((X-E(X))(Y-E(Y)\)의 평균값인 두 변수의 공분산은 0보다 작은 값을 갖게 된다.
그런데 \((X,Y)\)의 자료 중 \((X-E(X))\)와 \((Y-E(Y))\)의 부호가 같은 자료들이 많다는 것은 그림 2.1에서 1구역과 3구역에 대부분의 자료가 있다는 것을 의미하고 있기 때문에 한 변수의 값이 증가하거나 감소하면 다른 변수의 값도 함께 증가하거나 감소하는 ’양의 관계’에 있다는 것을 알 수 있다. 또한 \((X,Y)\)의 자료 중 \((X-E(X))\)와 \((Y-E(Y))\)의 부호가 반대인 자료들이 많다는 것은 그림 2.1에서 2구역과 4구역에 대부분의 자료가 있다는 것을 의미하는 것이고, 따라서 한 변수의 값이 증가하거나 감소하면 다른 변수의 값은 정반대의 방향으로 움직이는 ’음의 관계’에 있다는 것을 알 수 있다.
이러한 관련성으로 두 변수의 공분산이 큰 양수 값이면 두 변수의 관계는 강한 양의 관계가 있음을 알 수 있으며, 큰 음수의 값을 취하고 있으면 강한 음의 관계가 있음을 알 수 있다. 그러나 공분산의 값은 변수가 취하는 값 자체의 절대적 크기에도 영향을 받고 있기 때문에 스케일이 다른 자료에 대한 비교는 의미가 없게 된다. 이 문제는 공분산을 두 변수의 표준편차를 나누는 것으로 해결될 수 있으며, 이것이 상관계수가 된다.

그림 2.1: 두 변수 X와 Y의 공분산 구성요소
2.2 회귀계수의 최소제곱추정
식 (2.1)을 이용해서 \(Y\) 의 변동을 설명하고 예측하려면, 값이 알려져 있지 않는 모수 \(\beta_{0}\) 와 \(\beta_{1}\) 을 추정해야 한다. 두 변수 \(Y\) 와 \(X\) 에 대해 관측된 \(n\) 개의 자료를 \((y_{1},x_{1})\), \((y_{2}, x_{2})\), \(\ldots\), \((y_{n}, x_{n})\) 이라고 하자. 두 모수 \(\beta_{0}\) 와 \(\beta_{1}\) 의 추정은 \(n\) 개의 자료를 가장 잘 설명할 수 있는 직선을 구하는 과정이라고 할 수 있는데, ’자료를 가장 잘 설명하는 직선’이란 자료와 직선 사이에 간격이 가장 작은 직선이라고 볼 수 있다. 최소제곱추정법은 이런 개념을 활용한 추정법이며, 선형회귀모형에서 가장 널리 사용되는 회귀계수의 추정방법이다.
2.2.1 모수 \(\beta_{0}\)와 \(\beta_{1}\)의 추정
두 모수의 추정값을 \(\hat{\beta}_{0}\) 과 \(\hat{\beta}_{1}\) 라고 하면, \(X\) 변수의 \(i\) 번째 관찰값에 대한 \(Y\) 변수의 \(i\) 번째 예측값은 \(\hat{y}_{i} = \hat{\beta}_{0} + \hat{\beta}_{1}x_{i}\) 가 된다. \(Y\) 변수의 관찰값인 \(y_{i}\) 와 예측값인 \(\hat{y}_{i}\) 의 차이인 \(y_{i}-\hat{y}_{i}\) 는 자료와 회귀직선 사이의 거리가 되는데, 이것을 잔차(residual)라고 하며, \(e_{i}\) 로 표시한다.
따라서 \(\hat{\beta}_{0}\) 과 \(\hat{\beta}_{1}\) 은 다음에 주어지는 잔차의 제곱합(Residual sum of squares; RSS)을 최소화시키도록 구해야 한다.
\[\begin{equation} RSS = \sum_{i=1}^{n} \left( y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1}x_{i} \right)^{2} \tag{2.3} \end{equation}\]식 (2.3)의 RSS를 최소화시키는 추정값 \(\hat{\beta}_{0}\) 과 \(\hat{\beta}_{1}\) 을 구하기 위해서, RSS를 \(\hat{\beta}_{0}\) 과 \(\hat{\beta}_{1}\) 에 대하여 각각 편미분을 실시해서 얻은 두 개의 방정식은 다음과 같다.
\[\begin{align} \frac{\partial RSS}{\partial \hat{\beta}_{0}} & = -2 \sum_{i=1}^{n}(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1}x_{i}) = 0\\ \frac{\partial RSS}{\partial \hat{\beta}_{1}} & = -2 \sum_{i=1}^{n}x_{i}(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1}x_{i}) = 0 \tag{2.4} \end{align}\]식 (2.4)을 정리하면 다음과 같다.
\[\begin{align} \sum_{i=1}^{n}y_{i} & = n \hat{\beta}_{0} + \hat{\beta}_{1} \sum_{i=1}^{n}x_{i} \\ \sum_{i=1}^{n}x_{i}y_{i} & = \hat{\beta}_{0}\sum_{i=1}^{n}x_{i} + \hat{\beta}_{1}\sum_{i=1}^{n}x_{i}^{2} \tag{2.5} \end{align}\]식 (2.5)를 \(\hat{\beta}_{0}\) 과 \(\hat{\beta}_{1}\) 에 대하여 정리하면 각각 다음의 결과를 얻게 된다.
\[\begin{align} \hat{\beta}_{1} &= \frac{\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}} \\ \hat{\beta}_{0} &= \overline{y}-\hat{\beta}_{1}\overline{x} \tag{2.6} \end{align}\]단, \(\overline{y}\) 와 \(\overline{x}\) 는 표본평균이다.
추정된 회귀직선의 기울기인 \(\hat{\beta}_{1}\)의 의미는 설명변수를 한 단위 증가시켰을 때 반응변수의 평균 변화량의 추정값이 되어서, \(\hat{\beta}_{1}>0\)이면 설명변수 값의 증가가 반응변수 값의 증가로 연결되는 관계를 의미하고, 반면에 \(\hat{\beta}_{1}<0\)이면 설명변수 값의 증가가 반응변수 값의 감소로 연결되는 관계를 의미한다. 절편인 \(\hat{\beta}_{0}\) 은 설명변수의 값이 0일 때, 반응변수의 평균값의 추정값이 되는데, 만일 설명변수의 값 범위에 0이 포함되지 않는다면 특별한 의미를 부여하기는 어렵다.
식 (2.1)에 포함된 오차항 \(\varepsilon_{i}\)는 자료를 통해서 관측될 수 없는 변량이다. 하지만 회귀모형에서는 오차항에 대해 몇 가지 가정을 하고 있으며, 이 가정이 만족되지 않는 자료를 대상으로 식 (2.1)의 회귀모형을 적용시켜 분석하게 되면, 그 결과에 심각한 문제가 발생할 수 있다. 따라서 가정 만족 여부를 확인하는 것은 매우 중요한 분석 과정이 되는데, 이 경우 오차항 대신 사용할 수 있는 것이 잔차이다. 잔차분석에 대해서는 5장에서 살펴보겠다.
\(\bullet\) 예제 2.1: 모집단 회귀직선과 추정된 회귀직선
모집단 회귀직선과 오차항의 분포는 일반적으로 알려져 있지 않지만, 회귀모형의 의미를 살펴보기 위해서 \(E(Y|X)=5+2X\) 라고 가정하고, 오차항 \(\varepsilon\)은 평균이 0이고 분산이 1인 표준정규분포라고 가정하자.
설명변수의 값이 1, 4, 2, 7, 12, 6, 0, 3, 5, 8, 7 로 주어졌을 때, 표준정규분포에서 발생시킨 오차값을 추가해서 반응변수의 값을 생성해 보자.
단순선형회귀모형을 자료에 적합시켜서 절편과 기울기를 추정하고 모집단 회귀직선과 비교해 보자.
주어진 설명변수의 값에 대해 정규 난수를 추가한 반응변수 값을 생성해서 데이터 프레임으로 만들어 보자. 표준정규분포에서 난수 생성은 함수 rnorm()으로 수행할 수 있다.
library(tidyverse)
set.seed(12)
df2.1 <- tibble(x = c(1, 4, 2, 7, 12, 6, 0, 3, 5, 8, 7),
y = 5 + 2*x + rnorm(n = length(x))
)생성된 모의자료는 다음과 같다.
df2.1
## # A tibble: 11 × 2
## x y
## <dbl> <dbl>
## 1 1 5.52
## 2 4 14.6
## 3 2 8.04
## 4 7 18.1
## 5 12 27.0
## 6 6 16.7
## 7 0 4.68
## 8 3 10.4
## 9 5 14.9
## 10 8 21.4
## 11 7 18.2선형화귀모형의 적합은 함수 lm()으로 할 수 있으며, 일반적인 사용법은 lm(formula, data, ...)이다. formula는 설정된 회귀모형을 나타내는 R 모형 공식으로써, 단순회귀모형의 경우에는 y ~ x와 같이 물결표(~)의 왼쪽에는 반응변수, 오른쪽에는 설명변수를 두면 된다. R 모형 공식에 대해서는 다중회귀모형에서 더 자세하게 살펴보겠다. data는 회귀분석에 사용될 데이터 프레임을 지정하는 것으로써, 이 예제에서는 위에서 생성한 데이터 프레임 df2.1를 지정하면 된다.
모의자료가 있는 데이터 프레임 df2.1를 대상으로 단순회귀모형을 함수 lm()으로 적합시켜보자. 적합 결과는 \(\hat{y} = 4.764 + 1.948x\) 임을 알 수 있다.
fit2.1 <- lm(y ~ x, data = df2.1)
fit2.1
##
## Call:
## lm(formula = y ~ x, data = df2.1)
##
## Coefficients:
## (Intercept) x
## 4.764 1.948함수 lm()으로 생성된 객체 fit2.1을 단순하게 출력시키면 추정된 회귀계수만 나타나지만, 사실 객체 fit2.1은 다음과 같이 많은 양의 정보가 담겨 있는 리스트 객체이다.
names(fit2.1)
## [1] "coefficients" "residuals" "effects" "rank"
## [5] "fitted.values" "assign" "qr" "df.residual"
## [9] "xlevels" "call" "terms" "model"사용자마다 필요한 정보가 서로 다를 수 있기 때문에 SAS나 SPSS에서와 같이 모든 결과물을 한 번에 출력하는 것은 좋은 방법이 아닐 수 있다. 객체 fit2.1에 담겨 있는 필요한 정보를 획득하기 위해서는 해당하는 함수를 사용해야 하며, 앞으로 차근차근 살펴보겠다.
모집단 회귀직선 및 생성된 모의자료, 그리고 추정된 회귀직선을 함께 나타낸 그래프가 그림 2.2이다. 추정된 회귀직선은 모집단 회귀직선과 매우 비숫하지만 완벽하게 일치하지 않음을 알 수 있다.
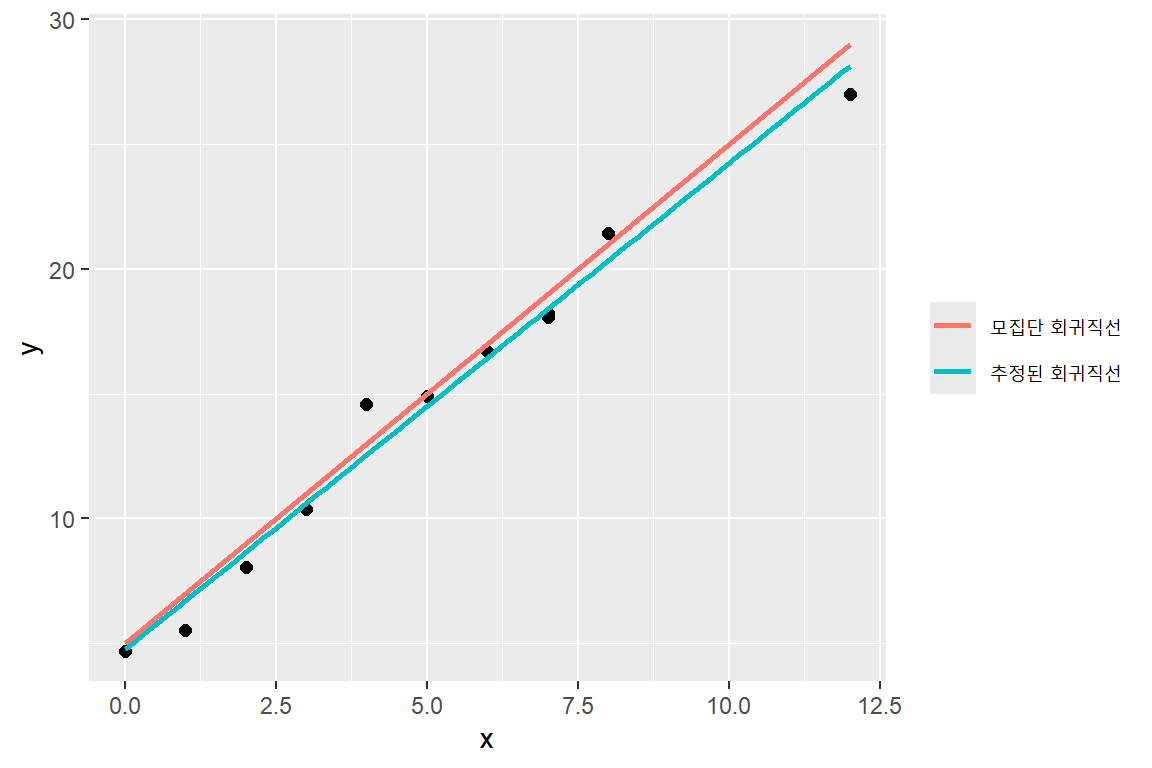
그림 2.2: 예제 2.1에서 사용된 모의자료와 회귀직선
\(\bullet\) 예제 2.2: 매출액에 대한 광고효과 분석
피자 전문 체인점 영업부서에서는 매출액에 대한 광고효과를 분석하기 위하여 유사한 인구분포를 갖는 20개 판매지역의 매출액 규모와 광고비 지출에 대한 자료를 수집하였다. 수집된 자료는 파일 ex2-2.csv에 입력되었고, 자료의 단위는 100만원이다.
매출액 규모와 광고비 지출 사이의 산점도를 작성하고, 두 변수 사이의 관계를 살펴보자.
최소제곱법에 의한 단순회귀직선을 추정하고, 추정된 \(\hat{\beta}_{1}\)의 의미를 해석해 보자.
자료가 콤마로 구분된 CSV 파일을 함수 readr::read_csv()로 불러와서 두 변수의 산점도를 작성해 보자.
df2.2 <- readr::read_csv("Data/ex2-2.csv")
df2.2
## # A tibble: 20 × 2
## sales advertisement
## <dbl> <dbl>
## 1 425 23
## 2 370 21
## 3 200 16
## 4 580 34
## 5 620 32
## 6 650 36
## 7 700 40
## 8 490 37
## 9 610 35
## 10 290 20
## 11 320 20
## 12 350 21
## 13 400 23
## 14 517 21
## 15 545 30
## 16 590 32
## 17 711 39
## 18 650 37
## 19 740 41
## 20 660 38ggplot(df2.2, aes(x = advertisement, y = sales)) +
geom_point(size = 2) +
geom_smooth(se = FALSE, aes(color = "비모수적 회귀곡선")) +
geom_smooth(method = "lm", se = FALSE, aes(color = "회귀직선")) +
labs(color = NULL)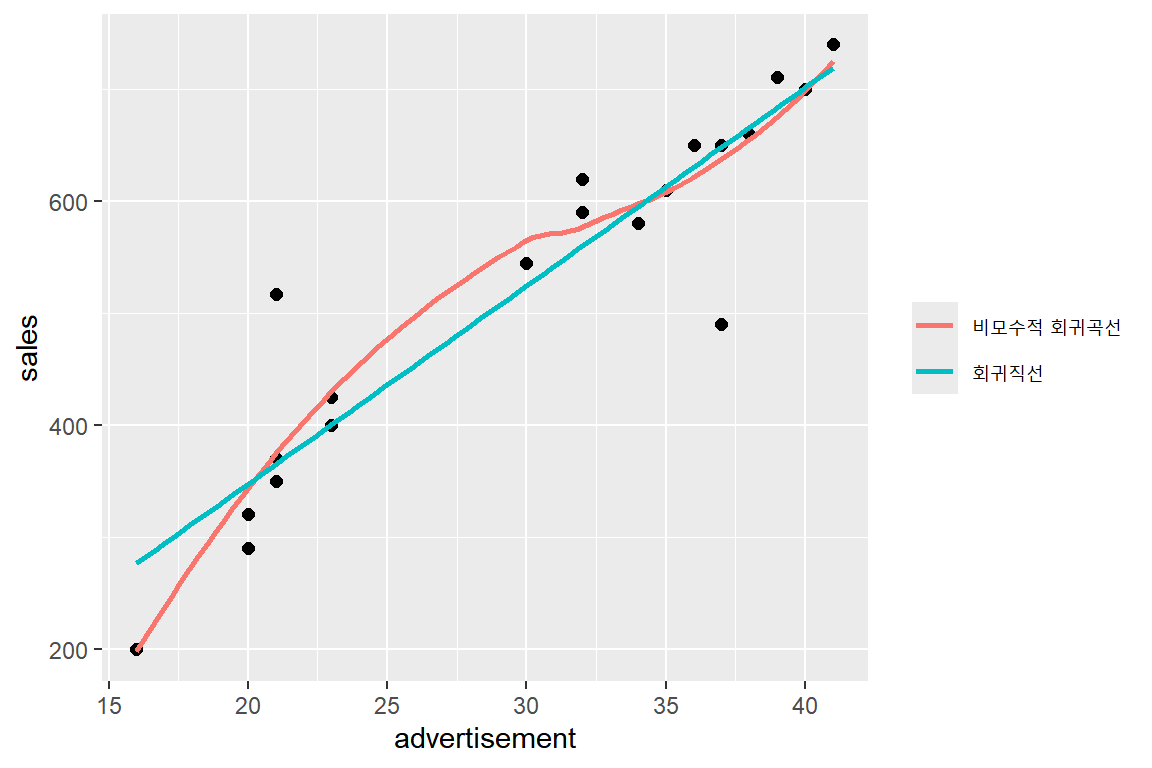
그림 2.3: 예제 2.2 자료의 산점도와 비모수적 회귀곡선
비모수적 회귀곡선은 두 변수의 관계를 가장 잘 나타내는 곡선을 추정하는 기능을 가지고 있다. 그림 2.3에 작성된 비모수적 회귀곡선은 대체로 직선의 형태를 취하고 있음을 알 수 있으며, 함께 표시된 회귀직선과 큰 차이가 없는 것을 알 수 있다. 이것으로 두 변수의 관계를 직선으로 설정하는 데에 큰 무리가 없음을 알 수 있다.
함수 lm()으로 단순회귀직선을 추정해 보자.
fit2.2 <- lm(sales ~ advertisement, data = df2.2)
fit2.2
##
## Call:
## lm(formula = sales ~ advertisement, data = df2.2)
##
## Coefficients:
## (Intercept) advertisement
## -6.944 17.713적합 결과는 \(\hat{y} = -6.994 + 17.713x\) 임을 알 수 있다. 추정된 직선의 기울기 \(\hat{\beta}_{1}=17.713\) 의 의미는 광고비 지출을 한 단위인 100만원 증가시키면 평균 매출액의 규모가 17.713백만원 증가한다는 것이 된다. 절편 \(\hat{\beta}_{0}=-6.994\) 의 의미는 광고비 지출이 \(0\) 일 때 평균 매출액은 -6.994백만원이라는 것이 된다. 즉, 광고를 하지 않으면 적자를 본다는 것인데, 이러한 해석은 조사된 광고비 자료의 범위에 \(0\) 이 포함되어 있지 않기 때문에 적절하지 않다고 하겠다.
2.2.2 최소제곱추정량의 특성
식 (2.1)에서 설정된 단순회귀모형에서 모수 \(\beta_{0}\)와 \(\beta_{1}\)의 최소제곱추정량인 \(\hat{\beta}_{0}\)과 \(\hat{\beta}_{1}\)은 몇 가지 중요한 통계적 특성을 갖는다.
첫 번째 특성은 식 (2.6)의 \(\hat{\beta}_{0}\)과 \(\hat{\beta}_{1}\)은 반응변수 \(Y_{i}\)의 선형결합으로 표시된다는 것이다. 먼저 \(\hat{\beta}_{1}\)의 경우를 살펴보자.
\[\begin{align} \hat{\beta}_{1} & = \frac{\sum_{i=1}^{n}(X_{i}-\overline{X})(Y_{i}-\overline{Y})}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}} \\ & = \frac{\sum_{i=1}^{n}(X_{i}-\overline{X})Y_{i}-\sum_{i=1}^{n}(X_{i}-\overline{X})\overline{Y}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}} \\ & = \frac{\sum_{i=1}^{n}(X_{i}-\overline{X})Y_{i}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}} \\ & = \sum_{i=1}^{n}\left(\frac{X_{i}-\overline{X}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right)Y_{i} \\ & = \sum_{i=1}^{n}c_{i}Y_{i} \tag{2.7} \end{align}\]단, \(c_{i} = (X_{i}-\overline{X})/\sum(X_{i}-\overline{X})^{2}\).
\(\hat{\beta}_{0}\)의 경우에는 \(\overline{Y}-\hat{\beta}_{1}\overline{X}\)의 표현식에서 \(\hat{\beta}_{1}\)이 \(Y_{i}\)의 선형결합이기 때문에 자연스럽게 \(Y_{i}\)의 선형결합으로 표시됨을 알 수 있다.
두 번째 특성은 최소제곱추정량이 불편추정량(unbiased estimator)이라는 것이다. 불편추정량이란 추정량의 기대값이 추정하려는 모수와 일치하는 추정량을 의미한다. 먼저 \(\hat{\beta}_{1}\)의 기대값을 구해보자.
\[\begin{align} E\left(\hat{\beta}_{1}\right) & = E\left(\sum_{i=1}^{n}c_{i}Y_{i}\right) \\ & = \sum_{i=1}^{n}c_{i}E(Y_{i}) \\ & = \sum_{i=1}^{n}c_{i}E(\beta_{0}+\beta_{i}X_{i}+\varepsilon_{i}) \\ & = \beta_{0}\sum_{i=1}^{n}c_{i}+\beta_{1}\sum_{i=1}^{n}c_{i}X_{i} \tag{2.8} \end{align}\]\(\sum c_{i}\)의 값은 다음과 같이 구할 수 있다.
\[\begin{equation} \sum_{i=1}^{n} c_{i} = \frac{\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)}{\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}} = 0 \tag{2.9} \end{equation}\]또한 \(\sum c_{i}X_{i}\)의 값은 다음과 같이 구할 수 있다.
\[\begin{align} \sum_{i=1}^{n}c_{i}X_{i} & = \frac{\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)X_{i}}{\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}} \\ & = \frac{\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)\left(X_{i}-\overline{X}\right)}{\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}} \\ & = \frac{\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}}{\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}} \\ & = 1 \tag{2.10} \end{align}\]식 (2.8)의 마지막 식에서 식 (2.9)와 식 (2.10)의 결과를 적용하면 다음의 결과를 얻게 된다.
\[\begin{equation} E\left(\hat{\beta}_{1}\right) = \beta_{1} \tag{2.11} \end{equation}\]이제 \(\hat{\beta}_{0}\)의 기대값을 유도해서 불편추정량임을 보이자.
\[\begin{align} E\left(\hat{\beta}_{0}\right) & = E\left(\overline{Y}-\hat{\beta}_{1}\overline{X}\right) \\ & = \frac{1}{n}\sum_{i=1}^{n}E(Y_{i})-\overline{X}E\left(\hat{\beta}_{1}\right) \\ & = \frac{1}{n}\sum_{i=1}^{n}(\beta_{0}+\beta_{1}X_{i}) - \overline{X}\beta_{1} \\ & = \beta_{0}+\beta_{1}\overline{X}-\overline{X}\beta_{1} \\ & = \beta_{0} \tag{2.12} \end{align}\]불편추정량인 \(\hat{\beta}_{0}\)과 \(\hat{\beta}_{1}\)의 분산을 유도해 보자. 식 (2.7)으로 \(\hat{\beta}_{1}\)은 \(\sum c_{i}Y_{i}\)로 표시할 수 있는데, \(Y_{i}\)가 서로 독립이기 때문에 \(\hat{\beta}_{1}\)의 분산은 다음과 같이 유도할 수 있다.
\[\begin{align} Var\left(\hat{\beta}_{1}\right) & = \sum_{i=1}^{n}c_{i}^{2}Var(Y_{i}) \\ & = \sigma^{2}\sum_{i=1}^{n}c_{i}^{2} \\ & = \sigma^{2}\sum_{i=1}^{n}\left(\frac{(X_{i}-\overline{X})}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right)^{2} \\ & = \sigma^{2}\frac{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}{\left(\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}\right)^{2}} \\ & = \frac{\sigma^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}} \tag{2.13} \end{align}\]\(\hat{\beta}_{0}\)의 분산은 다음과 같이 유도할 수 있다.
\[\begin{align} Var\left(\hat{\beta}_{0}\right) & = Var\left(\overline{Y}-\hat{\beta}_{1}\overline{X}\right) \\ & = Var\left(\overline{Y}\right) + \overline{X}^{2}Var\left(\hat{\beta}_{1}\right)-2\overline{X}Cov\left(\overline{Y},\hat{\beta}_{1}\right) \\ & = \frac{\sigma^{2}}{n} + \overline{X}^{2}\frac{\sigma^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}} \\ & = \sigma^{2}\left(\frac{1}{n}+\frac{\overline{X}^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right) \tag{2.14} \end{align}\]\(\overline{Y}\)와 \(\hat{\beta}_{1}\)의 공분산이 0임을 보이는 것은 연습문제로 남겨두겠다.
지금까지 살펴본 최소제곱추정량의 특성과 관련된 중요한 결과가 바로 가우스-마코프(Gauss-Markov) 정리이다. 가우스-마코프 정리는 최소제곱추정량으로 회귀계수를 추정해서 사용할 수 있는 근거를 제시하고 있다.
정리 2.1 (Gauss-Markov 정리) 오차항의 평균이 0, 분산이 \(\sigma^{2}\)이며 서로 독립을 가정한 회귀모형에서 최소제곱추정량은 최량선형불편추정량(Best Linear Unbiased Estimator: BLUE)이다. 즉, 최소제곱추정량은 \(Y_{i}\)의 선형결합으로 표시되는 모든 불편추정량 중에 최소 분산을 갖는다.
\(\bullet\) 최소제곱추정량으로 추정된 회귀직선의 특성
최소제곱추정량으로 추정된 회귀직선은 다음과 같은 몇 가지 유용한 특성을 가지고 있다.
- 절편을 포함한 회귀모형에서 잔차의 합은 항상 0이다. 이 특성은 식 (2.3)의 RSS를 \(\hat{\beta}_{0}\)으로 편미분한 식 (2.4)의 첫 번째 방정식에서 바로 확인할 수 있다.
\[\begin{equation} \sum_{i=1}^{n}(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1}x_{i}) = \sum_{i=1}^{n}(y_{i}-\hat{y}_{i}) = \sum_{i=1}^{n}e_{i} = 0 \tag{2.15} \end{equation}\]
관측값 \(y_{i}\)의 합과 추정값 \(\hat{y}_{i}\)의 합은 동일하다. 이 특성은 식 (2.15)에서 확인할 수 있다.
추정된 회귀직선은 항상 표본평균점 \((\overline{x}, \overline{y})\)을 항상 통과한다. 이 특성은 다음의 수식으로 확인할 수 있다. 마지막 수식에서 \(x=\overline{x}\) 가 되면, \(\hat{y}=\overline{y}\) 가 되기 때문에 추정된 회귀직선은 \((\overline{x}, \overline{y})\)을 항상 통과하게 된다.
\[\begin{align*} \hat{y} & = \hat{\beta}_{0} + \hat{\beta}_{1}x \\ & = (\overline{y}-\hat{\beta}_{1}\overline{x}) + \hat{\beta}_{1}x \\ & = \overline{y} + \hat{\beta}_{1}(x-\overline{x}) \end{align*}\]
- 잔차의 \(x_{i}\)에 대한 가중합은 0이다. 이 특성은 식 (2.3)의 RSS를 \(\hat{\beta}_{1}\)으로 편미분한 식 (2.4)의 두 번째 방정식에서 바로 확인할 수 있다.
\[\begin{align*} \sum_{i=1}^{n}x_{i}(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1}x_{i}) & = \sum_{i=1}^{n}x_{i}y_{i}-\sum_{i=1}^{n}x_{i}(\hat{\beta}_{0}+\hat{\beta}_{1}x_{i}) \\ & = \sum_{i=1}^{n}x_{i}y_{i} - \sum_{i=1}^{n}x_{i}\hat{y}_{i} \\ & = \sum_{i=1}^{n}x_{i}(y_{i}-\hat{y}_{i}) \\ & = \sum_{i=1}^{n}x_{i}e_{i} = 0 \end{align*}\]
- 잔차의 \(\hat{y}_{i}\)에 대한 가중합은 0이다. 이 특성은 다음의 수식으로 확인할 수 있다.
\[\begin{align*} \sum_{i=1}^{n}\hat{y}_{i}e_{i} & = \sum_{i=1}^{n}(\hat{\beta}_{0} + \hat{\beta}_{1}x_{i})e_{i} \\ & = \hat{\beta}_{0}\sum_{i=1}^{n}e_{i} + \hat{\beta}_{1}\sum_{i=1}^{n}x_{i}e_{i} \\ & = 0 \end{align*}\]
2.3 오차분산 \(\sigma^{2}\)의 추정
회귀계수 \(\beta_{0}\)과 \(\beta_{1}\)의 구간추정 및 가설검정을 실시하는 경우와 설명변수의 주어진 값에 대한 반응변수 값의 예측구간 추정 등을 실시하는 경우에는 오차항의 분산인 \(\sigma^{2}\)의 추정값이 반드시 필요하다.
식 (1.1)의 회귀모형에서 회귀모형 \(f(X)\)의 실제 형태는 일반적으로 알려져 있지 않으며, 주어진 자료를 근거로 식 (1.3)와 같은 함수형태를 가정하게 된다. 이 때 가정한 함수형태의 적절성 여부와 관계 없이 오차항의 분산을 정확하게 추정할 수 있다면 가장 이상적인 상황이 될 것이다. 그러나 이것은 하나의 \(X\) 변수의 값에 대하여 여러 개의 \(Y\) 변수의 값이 있는 경우에만 가능한 상황이며, 현실적으로는 접하기 어려운 상황이 된다.
따라서 일반적으로 사용하는 방법은 잔차의 분산으로 오차항의 분산을 추정하는 것이다. 잔차의 평균은 0이기 때문에 잔차의 분산은 잔차제곱합(residual sum of squares; RSS)으로 표현된다.
\[\begin{equation} RSS = \sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2} \tag{2.16} \end{equation}\]
회귀모형의 추론 과정에는 잔차제곱합과 같은 형태의 몇 가지 제곱합이 사용된다. 이러한 제곱합은 모두 ’자유도’를 갖게 되는데, 각 제곱합의 자유도는 다음 두 가지 방법 중 적용 가능한 방법으로 구할 수 있다.
변수의 합이 주어진 경우: 예를 들어 \(x_{1}+x_{2}+x_{3}=0\) 이라는 조건에서 자유롭게 값을 선택할 수 있는 변수의 개수는 2개가 된다. 그것은 만일 \(x_{1}\)과 \(x_{2}\)의 값이 선택되면 \(x_{3}\)의 값은 자동으로 구해지기 때문이다. 표본분산의 경우 적용되는 제곱합의 형태는 \(\sum_{i=1}^{n}(y_{i}-\overline{y})^{2}\)이 되는데, \(\sum_{i=1}^{n}(y_{i}-\overline{y})=0\) 이라는 조건이 있기 때문에 자유도는 \(n-1\)이 된다.
추정량이 포함된 경우: 자유도는 통계학에서 일종의 화폐와 같은 역할을 한다. 수집되는 각 자료마다 하나의 자유도가 추가되는 반면에, 모수에 대한 추정에 이루어질 때마다 하나의 자유도가 차감되는 것이다. 식 (2.16)의 잔차제곱합에서는 \(n\)개의 \(y_{i}\)가 수집되지만 \(\hat{y}_{i}\)를 얻기 위해서는 두 모수 \(\beta_{0}\)와 \(\beta_{1}\)에 대한 추정이 이루어져 2개의 자유도를 잃게 된다. 따라서 잔차제곱합의 자유도는 \(n-2\)가 된다.
식 (2.16)의 잔차제곱합 \(RSS\)의 기대값은 \(E(RSS)=(n-2)\sigma^{2}\)가 되는데, 이것은 \(RSS/\sigma^{2}\) 가 자유도가 \(n-2\) 인 카이제곱 분포를 하고 있으며, 카이제곱 분포를 하는 확률변수의 기대값은 자유도가 된다는 결과에 의해서 \(E(RSS/\sigma^{2})=n-2\) 가 되기 때문이다. 따라서 오차항의 분산인 \(\sigma^{2}\)의 불편추정량은 다음과 같이 정의된다.
\[\begin{equation} \hat{\sigma}^{2} = \frac{RSS}{n-2} = MSE \tag{2.17} \end{equation}\]
\(\sigma^{2}\) 의 추정량인 \(MSE\)는 잔차제곱평균이라고 하며, \(\sigma\) 의 추정량인 \(\sqrt{MSE}\)는 회귀 표준오차(standard error of regression)라고 한다. 추정량 \(MSE\)는 잔차를 기반으로 오차항의 분산을 추정하는 것이기 때문에 식 (1.3)에서 가정한 함수 형태가 적절해야 하는 것은 필수적이다. 또한 오차항의 가정 사항도 모두 만족되어야 \(\sigma^{2}\)의 좋은 추정량이 될 수 있다. 만일 이러한 가정 사항이 만족되지 않는다면, \(\sigma^{2}\)의 추정량으로서 \(MSE\)의 유용성은 매우 떨어진다고 할 수 있다.
\(\bullet\) 예제 2.3: 매출액에 대한 광고효과 분석
예제 2.2의 자료 ex2-2.csv에 대하여 다음의 분석을 실시해 보자.
예제 2.2에서 구한 회귀직선으로 주어진 광고비 지출자료에 대한 평균적인 매출액을 추정하고, 잔차를 구하자.
\(\sigma\) 의 추정값인 회귀 표준오차를 구해 보자.
예제 2.2에서 이루어진 분석을 다시 실행해 보자.
함수 lm()으로 생성된 리스트 객체 fit2.2에는 "fitted.values"와 "residuals"라는 이름으로 주어진 설명변수 값에 대한 반응변수의 추정값과 잔차가 입력되어 있다.
cbind(df2.2, Yhat = fit2.2$fitted, resid = fit2.2$resid)
## sales advertisement Yhat resid
## 1 425 23 400.4524 24.547619
## 2 370 21 365.0266 4.973389
## 3 200 16 276.4622 -76.462185
## 4 580 34 595.2941 -15.294118
## 5 620 32 559.8683 60.131653
## 6 650 36 630.7199 19.280112
## 7 700 40 701.5714 -1.571429
## 8 490 37 648.4328 -158.432773
## 9 610 35 613.0070 -3.007003
## 10 290 20 347.3137 -57.313725
## 11 320 20 347.3137 -27.313725
## 12 350 21 365.0266 -15.026611
## 13 400 23 400.4524 -0.452381
## 14 517 21 365.0266 151.973389
## 15 545 30 524.4426 20.557423
## 16 590 32 559.8683 30.131653
## 17 711 39 683.8585 27.141457
## 18 650 37 648.4328 1.567227
## 19 740 41 719.2843 20.715686
## 20 660 38 666.1457 -6.145658회귀모형의 다양한 추정 결과는 함수 lm()으로 생성된 객체를 함수 summary()에 입력하면 얻을 수 있다. 자세한 사용 방법은 3장에서 살펴볼 것이지만, 여기에서는 함수 summary()의 결과 중 \(\sigma\) 의 추정값만을 출력해 보자.
2.4 연습문제
1. 설명변수가 하나이고 반응변수와의 관계가 직선으로 가정할 수 있는 경우에 회귀모형은 다음과 같이 정의된다.
\[\begin{equation} y_{i} = \beta_{0} + \beta_{1}x_{i} + \varepsilon_{i}, ~~i = 1, \ldots, n \end{equation}\]
여기에서 \(y_{i}\) 는 반응변수의 \(i\) 번째 관찰값, \(x_{i}\) 는 설명변수의 \(i\) 번째 관찰값을 의미한다.
\(\beta_{0}\) 와 \(\beta_{1}\) 은 모수인데, 모수란 무엇인지 설명하고, 두 모수가 모형에서 어떤 역할을 하고 있는지 설명하라.
\(\varepsilon_{i}\) 는 모형의 오차항을 나타내는 변량이다. 모형에 오차항을 포함시킨 이유는 무엇이며, 어떤 가정을 하고 있는지 설명하라.
2. 단순회귀모형의 모수 \(\beta_{0}\) 와 \(\beta_{1}\) 의 최소제곱추정량을 각각 \(\hat{\beta}_{0}\) 와 \(\hat{\beta}_{1}\) 이라고 하자.
최소제곱추정량이란 무엇을 ’최소화’시키는 추정량이며, 어떤 의미를 지니고 있는지 설명하라.
최소제곱추정량 \(\hat{\beta}_{0}\) 와 \(\hat{\beta}_{1}\) 을 각각 유도하라.
최소제곱추정량 \(\hat{\beta}_{1}\) 의 표본분포를 유도하라.
3. Gauss-Markov 정리는 회귀모형에서 중요한 역할을 하고 있다.
Gauss-Markov 정리의 가정사항은 무엇인가?
Gauss-Markov 정리로 최소제곱추정량의 사용에 정당성이 부여되었다고 할 수 있는데, 그 이유는 무엇인가?
4. 단순회귀모형의 오차항 \(\varepsilon_{i}\) 의 분산 \(\sigma^{2}\) 를 추정하고자 한다.
오차항의 분산을 잔차의 제곱합을 이용해서 추정할 수밖에 없는 이유는 무엇인가?
잔차제곱합의 자유도는 무엇인가? 계산 과정을 설명하라.
오차항 분산 \(\sigma^{2}\) 의 불편추정량을 정의하라.