3 장 단순선형회귀모형의 추론

회귀모형의 추론에서 우리가 살펴볼 내용은 회귀계수에 대한 신뢰구간 추정 및 검정, 그리고 설명변수의 값이 주어졌을 때 반응변수의 조건부 평균에 대한 신뢰구간 추정 등이다.

이번 장에서 살펴볼 회귀모형은 다음의 단순회귀모형이다.

\[\begin{equation} Y_{i} = \beta_{0} + \beta_{1}X_{i} + \varepsilon_{i}, ~~i = 1, \ldots, n \tag{3.1} \end{equation}\]

2장에서 회귀계수를 최소제곱추정량으로 추정하기 위해서 필요한 가정은 다음과 같다.

\[\begin{equation} \varepsilon_{1}, \ldots, \varepsilon_{n} \text{은 서로 독립이고}~E(\varepsilon_{i})=0,~Var(\varepsilon_{i})=\sigma^{2} \end{equation}\]

회귀모형의 추론을 위해서는 위 가정에 정규분포 가정이 추가된 다음의 가정이 필요하게 된다.

\[\begin{equation} \varepsilon_{1}, \ldots, \varepsilon_{n} \stackrel{iid}{\sim} N(0,\sigma^{2}) \tag{3.2} \end{equation}\]

3.1 회귀계수 \(\beta_{1}\)에 대한 추론

식 (3.1)에서 회귀계수 \(\beta_{1}\)은 회귀직선의 기울기를 나타내는 모수로서, 설명변수 \(X\)를 한 단위 증가시켰을 때 반응변수 \(Y\)의 평균 변화량을 나타낸다. 회귀계수 \(\beta_{1}\)의 점추정량은 2장에서 살펴본 최소제곱추정량으로 구할 수 있었는데, 이번 절에서는 \(\beta_{1}\)의 신뢰구간 추정과 가설검정에 대해 살펴보고자 한다.

식 (3.1)으로 설정된 회귀모형이 주어진 자료를 적절하게 설명하고 있는지 여부는 점추정 결과만으로는 알 수 없다. 추정 결과의 정확성 또는 적절성 등에 대한 접근은 관련된 회귀계수의 신뢰구간 추정을 통해 확인할 수 있다. 또한 주어진 자료를 근거로 가설 \(H_{0}:\beta_{1}=0\) 에 대한 검정이 필요한데, 만일 가설을 기각할 수 없다면, 반응변수 \(Y\)와 설명변수 \(X\)의 관계가 식 (3.1)에서 설정한 선형관계로는 설명하기 어렵다는 것을 의미하기 때문이다.

이러한 추론을 실시하기 위해서는 회귀계수 \(\beta_{1}\)의 점추정량인 \(\hat{\beta}_{1}\)의 표본분포를 반드시 알고 있어야 한다.

3.1.1 \(\hat{\beta}_{1}\)의 표본분포

식 (3.1)의 회귀모형에 식 (3.2)에 주어진 오차항의 가정 사항을 적용시키면 설명변수 \(X_{i}\)가 주어졌을 때 반응변수 \(Y_{i}\)에 대한 분포는 다음과 같이 주어진다.

\[\begin{equation} Y_{i} \stackrel{iid}{\sim} N(\beta_{0}+\beta_{1}X_{i}, \sigma^{2}),~~i=1, \ldots, n \end{equation}\]

2장에서 유도한 회귀계수 \(\beta_{1}\)의 최소제곱추정량인 \(\hat{\beta}_{1}\)은 식 (2.7)에서 다음과 같이 반응변수 \(Y_{i}\)의 선형결합으로 표현됨을 보였다.

\[\begin{equation} \hat{\beta}_{1} = \sum_{i=1}^{n} c_{i}Y_{i},~~c_{i}= \frac{X_{i}-\overline{X}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}} \end{equation}\]

즉, \(\hat{\beta}_{1}\)은 정규분포를 하는 확률변수인 \(Y_{i}\)의 선형결합으로 표현되기 때문에 \(\hat{\beta}_{1}\)의 분포도 정규분포를 따르게 되는 것이다. 또한 식 (2.11)와 식 (2.13)에서 유도된 \(\hat{\beta}_{1}\)의 평균과 분산을 적용시키면 \(\hat{\beta}_{1}\)의 표본분포는 다음과 같이 주어진다.

\[\begin{equation} \hat{\beta}_{1} \sim N \left( \beta_{1}, \frac{\sigma^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}} \right) \tag{3.3} \end{equation}\]

3.1.2 \(\beta_{1}\)의 신뢰구간

모수 \(\beta_{1}\)에 대한 신뢰구간은 하나의 숫자보다는 모수를 포함할 구간을 제시하는 것이며, 구간의 폭은 추정량의 표준오차에 비례하여 결정된다. 따라서 주어진 자료가 설정된 회귀모형에 의하여 잘 설명된다면 신뢰구간의 폭은 상대적으로 작은 값을 갖게 된다.

모수 \(\beta_{1}\)의 신뢰구간은 모수의 불편추정량인 \(\hat{\beta}_{1}\)의 표본분포를 활용해서 유도되는데, 우선 식 (3.3)에서 다음의 결과를 얻을 수 있다.

\[\begin{equation} Z = \frac{\hat{\beta}_{1}-\beta_{1}}{\sqrt{\sigma^{2}/\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}} \sim N(0,1) \end{equation}\]

식 (2.17)에서 \(\sigma^{2}\)의 불편추정량은 \(MSE\)임이 확인되었고, 이제 \(\sigma^{2}\)를 \(MSE\)로 대체하면 다음의 결과를 얻게 된다.

\[\begin{equation} t = \frac{\hat{\beta}_{1}-\beta_{1}}{\sqrt{MSE/\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}} \sim t(n-2) \tag{3.4} \end{equation}\]

단, \(t(n-2)\)는 자유도가 \(n-2\)인 \(t\) 분포를 의미하는 것인데, 통계량 \(t\)의 자유도는 분모에 사용된 \(MSE\)의 자유도가 그대로 적용된다.

모수 \(\beta_{1}\)의 \(100 \times (1-\alpha)\)% 신뢰구간은 식 (3.4)을 이용해서 다음과 같이 유도된다.

\[\begin{align} 1-\alpha & = P \left( -t_{\alpha, n-2} < \frac{\hat{\beta}_{1}-\beta_{1}}{SE(\hat{\beta}_{1})} < t_{\alpha, n-2} \right) \\ & = P \left( \hat{\beta}_{1} - t_{\alpha, n-2} \cdot SE(\hat{\beta}_{1}) < \beta_{1} < \hat{\beta}_{1} + t_{\alpha, n-2} \cdot SE(\hat{\beta}_{1}) \right) \tag{3.5} \end{align}\]

단, \(SE(\hat{\beta}_{1})=\sqrt{MSE/\sum(X_{i}-\overline{X})^{2}}\) 를 나타내고, \(t_{\alpha, n-2}\) 는 자유도가 \(n-2\)인 \(t\) 분포에서 상위 \(100 \times \alpha\) 백분위수를 나타낸다.

모수의 신뢰구간은 점추정량의 표본분포를 근거로 유도된 것이기 때문에, 식 (3.5)의 신뢰구간도 표본분포의 개념을 이용해서 해석해야 한다. 즉, 자료에 주어진 동일한 \(X\) 값에 대해서 표본을 반복해서 추출하고, 추출된 각 표본마다 식 (3.5)에 의해 95% 신뢰구간을 계산한다면, 계산된 전체 신뢰구간 중 대략 95%의 신뢰구간에는 미지의 모수인 \(\beta_{1}\)이 포함되지만 나머지 5%의 신뢰구간에는 \(\beta_{1}\)이 포함되지 않을 수 있다는 것이다. 따라서 실제 상황에서 우리가 얻게 되는 하나의 표본을 대상으로 계산된 신뢰구간에는 \(\beta_{1}\)이 포힘되어 있는지 여부를 알 수 없는 것이다.

3.1.3 \(\beta_{1}\)에 대한 가설검정

기울기에 대한 가설검정은 \(\beta_{1}\) 이 특정한 상수인 \(\beta_{1o}\) 와 같은 값을 갖는지 여부에 대한 것이다.

\[\begin{equation} H_{0}:\beta_{1} = \beta_{1o}, ~~~H_{1}:\beta_{1} \ne \beta_{1o} \tag{3.6} \end{equation}\]

만일 \(\sigma^{2}\) 가 알려져 있다면, 검정통계량은 다음과 같이 주어지며,

\[\begin{equation} Z= \frac{\hat{\beta}_{1}-\beta_{1o}}{\sqrt{\sigma^{2}/\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}} \tag{3.7} \end{equation}\]

\(H_{0}\)이 사실인 경우, 분포는 \(N(0,1)\) 이 된다.

그러나 대부분의 상황에서는 \(\sigma^{2}\) 의 값을 알기 어렵고, 따라서 \(MSE\) 로 추정한 결과를 대신 사용하게 된다. 이 경우에 검정통계량은 다음과 같이 주어지며,

\[\begin{equation} t = \frac{\hat{\beta}_{1}-\beta_{1o}}{SE(\hat{\beta}_{1})} \tag{3.8} \end{equation}\]

단, \(SE(\hat{\beta}_{1}) = \sqrt{MSE/\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\).

\(H_{0}\)이 사실인 경우, 검정통계량의 분포는 \(t(n-2)\) 가 된다.

식 (3.6)의 가설 중 가장 중요한 경우는 \(\beta_{1o}=0\) 이 되며, 이것을 회귀계수 \(\beta_{1}\)의 유의성 검정이라고 한다.

\[\begin{equation} H_{0}:\beta_{1}=0,~~~H_{1}:\beta_{1} \ne 0 \tag{3.9} \end{equation}\]

\(\beta_{1}\)의 유의성 검정에서 사용되는 검정통계량은 식 (3.8)에서 \(\beta_{1o}\) 를 0으로 두는 형태가 된다.

\[\begin{equation} t = \frac{\hat{\beta}_{1}}{SE(\hat{\beta}_{1})} \tag{3.10} \end{equation}\]

주어진 자료를 근거로 만일 \(H_{0}\) 을 기각할 수 없다면, 식 (3.1)에서 설정된 모형이 \(Y_{i}=\beta_{0}+\varepsilon_{i}\) 로 변경되는 것이며, 따라서 설명변수 \(X\)가 반응변수 \(Y\)의 변동을 설명하는데 아무런 기여를 할 수 없다는 것을 의미하게 된다. 하지만 이것은 두 변수의 실제 관계가 선형이 아닌 경우에는 틀린 결론이 될 수 있다. 예시 자료를 활용해서 자세히 살펴보자.

그림 3.1은 두 변수 사이에 관계가 없는 경우에 대한 예시로서, 설명변수가 반응변수의 변동을 설명하는데 어떤 역할도 할 수 없는 상황으로 보인다. 파란 직선은 추정된 회귀직선을 나타내고 있는데, \(H_{0}:\beta_{1}=0\) 을 기각하기 어려운 상황으로 보인다. 실제 예시 자료를 근거로 가설 \(H_{0}:\beta_{1}=0, ~~H_{1}:\beta_{1} \ne 0\) 에 대한 검정을 실시한 결과 p-값은 0.859으로 계산되어 \(H_{0}\)은 기각할 수 없게 된다.

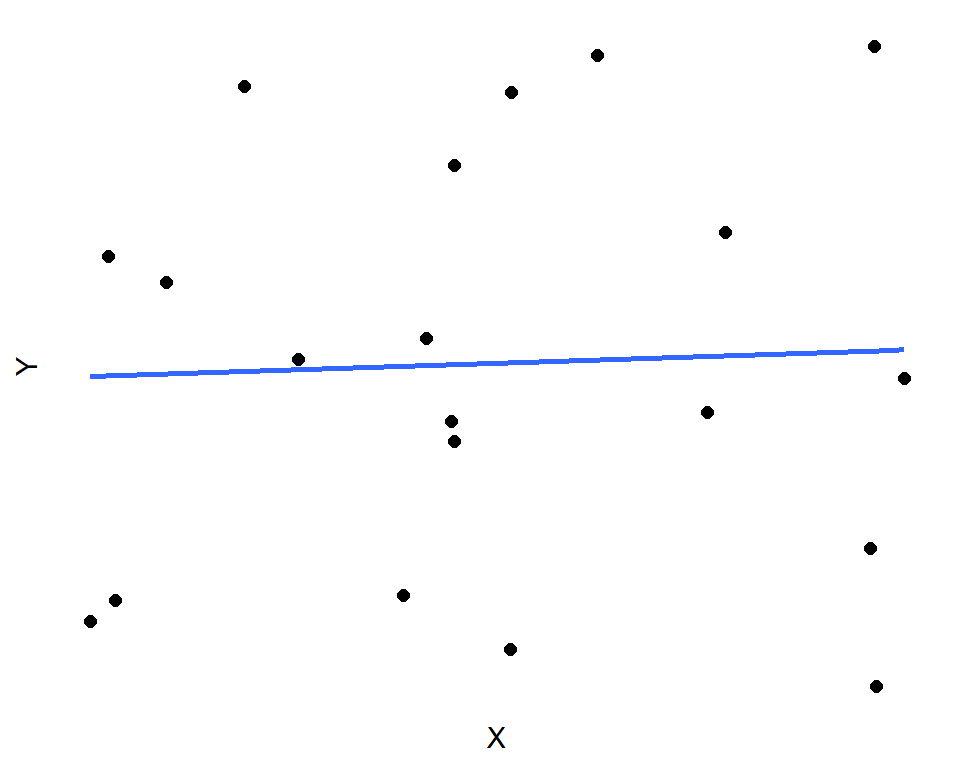
$H_{0}:\beta_{1}=0$을 기각할 수 없는 상황: 두 변수 사이에 관계가 없는 경우

그림 3.1: \(H_{0}:\beta_{1}=0\)을 기각할 수 없는 상황: 두 변수 사이에 관계가 없는 경우

그림 3.2는 두 변수의 관계가 선형이 아닌 2차 함수의 관계에 있는 경우에 대한 예시 자료이다. 추정된 기울기는 0에 가까운 값을 갖고 있고, 가설 \(H_{0}:\beta_{1}=0, ~~H_{1}:\beta_{1} \ne 0\) 에 대한 검정 결과 p-값은 0.839으로 계산되어 \(H_{0}\) 을 기각하기 어려운 상황으로 보이지만, 두 변수 사이에는 명확한 관계가 있는 것을 알 수 있다.

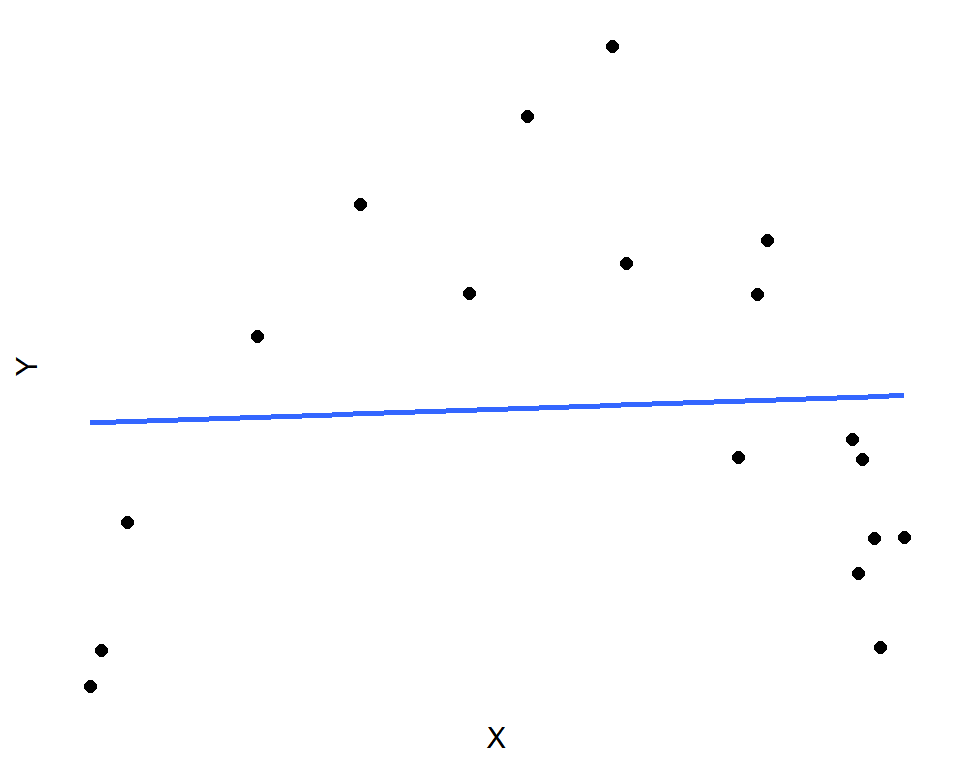
$H_{0}:\beta_{1}=0$을 기각할 수 없는 상황: 두 변수 사이에 2차 함수 관계가 있는 경우

그림 3.2: \(H_{0}:\beta_{1}=0\)을 기각할 수 없는 상황: 두 변수 사이에 2차 함수 관계가 있는 경우

그림 3.3도 두 변수의 관계가 선형이 아닌 2차 함수의 관계에 있는 경우에 대한 예시 자료이다. 이 경우에는 기울기의 추정 결과가 0.376으로 나오며, 검정 결과에서도 p-값이 0.0112로 계산되어서 유의수준 \(\alpha = 0.05\) 에서 \(H_{0}\)을 기각할 수 있는 자료이다. 하지만 \(X^{2}\)을 포함시킨 회구모형 \(Y=\beta_{0}+\beta_{1}X+\beta_{2}X^{2}+\varepsilon\) 이 더 적절한 모형으로 보인다.

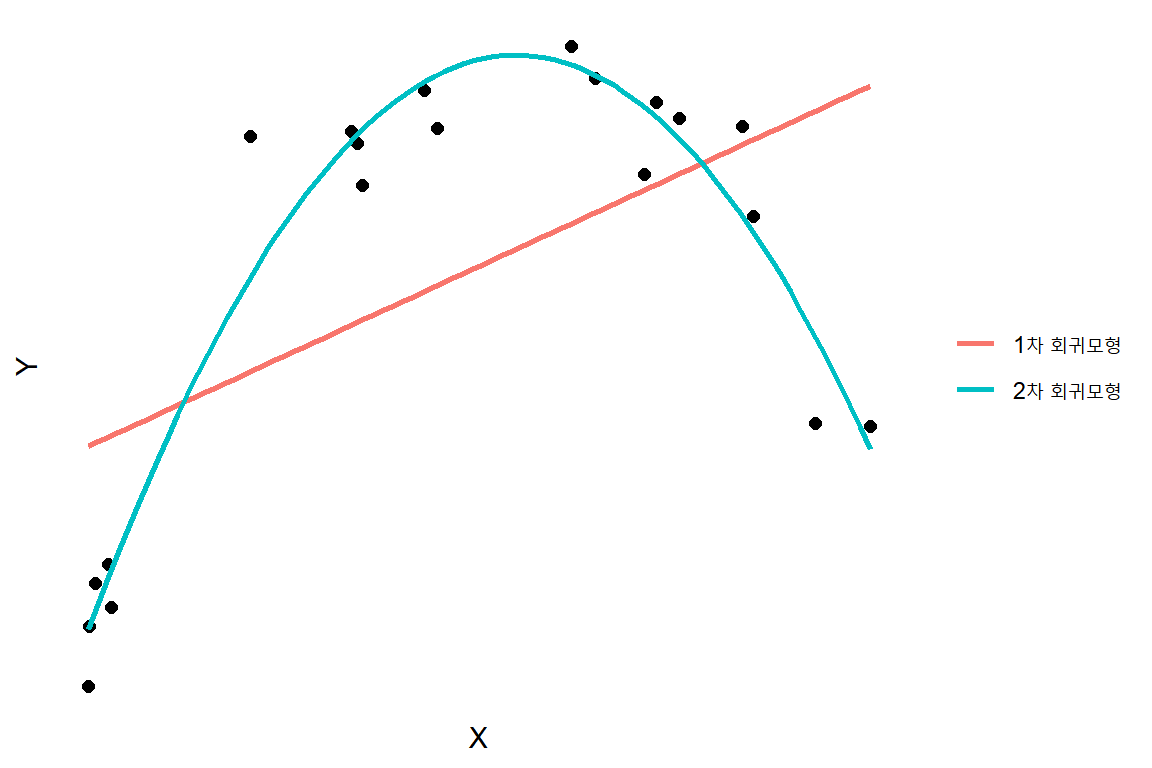
$H_{0}:\beta_{1}=0$을 기각할 수 있지만, $X^{2}$을 포함한 2차 회귀모형이 더 좋은 결과를 보이는 경우

그림 3.3: \(H_{0}:\beta_{1}=0\)을 기각할 수 있지만, \(X^{2}\)을 포함한 2차 회귀모형이 더 좋은 결과를 보이는 경우

3.2 회귀계수 \(\beta_{0}\)에 대한 추론

회귀계수 \(\beta_{0}\) 는 회귀직선의 Y축 절편을 나타내는 모수로서, 설명변수 \(X\) 의 값이 0일 때 반응변수 \(Y\)의 평균값을 나타낸다. 따라서 설명변수가 갖는 자료의 범위에 0이 포함되지 않는 경우에는 추론의 필요성이 크지 않은 모수가 된다. 또한 가설 \(H_{0}:\beta_{0}=0\) 을 기각할 수 없는 경우에도 일반적으로는 모형에서 \(\beta_{0}\) 를 제외시키지 않는다.

3.2.1 \(\hat{\beta}_{0}\) 의 표본분포

2장에서 살펴본 \(\beta_{0}\) 의 최소제곱추정량은 식 (2.6)에서 다음과 같이 유도되었다.

\[\begin{equation} \hat{\beta}_{0} = \overline{Y} - \hat{\beta}_{1} \overline{X} \end{equation}\]

\(\hat{\beta}_{1}\) 이 식 (2.7)에서 \(Y_{i}\) 의 선형결합으로 표현됨을 알 수 있기 때문에 \(\hat{\beta}_{0}\) 도 자연스럽게 \(Y_{i}\) 의 선형결합으로 표현됨을 알 수 있다. 따라서 \(\hat{\beta}_{0}\) 도 \(Y_{i}\) 와 같은 분포인 정규분포를 따르게 된다.

\(\hat{\beta}_{0}\) 의 평균과 분산은 식 (2.12)과 식 (2.14)에서 다음과 같이 유도되었다.

\[\begin{align*} E\left(\hat{\beta}_{0}\right) &= \beta_{0} \\ Var\left(\hat{\beta}_{0}\right) &= \sigma^{2}\left(\frac{1}{n}+\frac{\overline{X}^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right) \end{align*}\]

따라서 \(\hat{\beta}_{0}\) 의 표본분포는 다음과 같다.

\[\begin{equation} \hat{\beta}_{0} \sim N\left(\beta_{0},~ \sigma^{2}\left(\frac{1}{n}+\frac{\overline{X}^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right) \right) \end{equation}\]

3.2.2 \(\beta_{0}\)의 신뢰구간

모수 \(\beta_{0}\) 의 신뢰구간은 3.1.2절에서 \(\beta_{1}\)의 신뢰구간을 유도할 때 사용했던 것과 동일한 방식으로 유도할 수 있다. 우선 \(\beta_{0}\) 의 불편추정량인 \(\hat{\beta}_{0}\) 을 표준화시킨 통계량 \(t\) 는 다음과 같이 표현되며, 분포는 \(\hat{\beta}_{1}\) 의 경우와 동일하게 \(t(n-2)\)가 된다.

\[\begin{equation} t = \frac{\hat{\beta}_{0}-\beta_{0}}{\sqrt{MSE\left(\frac{1}{n}+\frac{\overline{X}^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right)}} \sim t(n-2) \tag{3.11} \end{equation}\]

모수 \(\beta_{0}\) 의 \(100 \times (1-\alpha)\)% 신뢰구간은 식 (3.11)을 이용하면 다음과 같이 유도된다.

\[\begin{align} 1-\alpha & = P \left( -t_{\alpha, n-2} < \frac{\hat{\beta}_{0}-\beta_{0}}{SE(\hat{\beta}_{0})} < t_{\alpha, n-2} \right) \\ & = P \left( \hat{\beta}_{0} - t_{\alpha, n-2} \cdot SE(\hat{\beta}_{0}) < \beta_{0} < \hat{\beta}_{0} + t_{\alpha, n-2} \cdot SE(\hat{\beta}_{0}) \right) \tag{3.12} \end{align}\]

단, \(SE(\hat{\beta}_{0})=\sqrt{MSE\left(\frac{1}{n}+\frac{\overline{X}^{2}}{\sum(X_{i}-\overline{X})^{2}}\right)}\) 을 나타내며, \(t_{\alpha, n-2}\) 는 자유도가 \(n-2\)인 \(t\) 분포에서 상위 \(100 \times \alpha\) 백분위수를 나타낸다.

3.2.3 \(\beta_{0}\)에 대한 가설검정

모수 \(\beta_{0}\) 에 대한 가설검정도 3.1.3절에서 살펴본 \(\beta_{1}\) 의 가설검정의 경우와 동일한 방식으로 진행할 수 있다. 다음의 가설에 대하여

\[\begin{equation} H_{0}: \beta_{0} = 0, ~~H_{1}: \beta_{0} \ne 0 \end{equation}\]

검정정통계량은 식 (3.11)을 근거로 다음과 같이 주어진다.

\[\begin{equation} t = \frac{\hat{\beta}_{0}}{SE(\hat{\beta}_{0})} \tag{3.13} \end{equation}\]

단, \(SE(\hat{\beta}_{0})=\sqrt{MSE\left(\frac{1}{n}+\frac{\overline{X}^{2}}{\sum(X_{i}-\overline{X})^{2}}\right)}\).

\(H_{0}\) 이 사실일 때 검정통계량은 분포는 \(t(n-2)\)가 된다.

절차는 \(\beta_{1}\) 의 경우와 동일하지만, 검정 결과의 적용 방식에는 큰 차이가 있다.

\(\beta_{0}\) 는 설명변수 \(X\) 의 값이 0일 때 반응변수 \(Y\)의 평균값을 나타내기 때문에, 설명변수가 갖는 자료의 범위에 0이 포함되지 않는 경우에는 추론의 필요성이 크지 않은 모수가 된다. 또한 가설 \(H_{0}:\beta_{0}=0\) 을 기각할 수 없는 경우에도 모형에서 \(\beta_{0}\) 를 제외시키지 않기 때문에, \(\beta_{0}\) 에 대한 가설검정은 일반적으로 무시된다고 할 수 있다.

만일 가설 \(H_{0}:\beta_{0}=0\) 의 검정 결과에 따라 모형에서 \(\beta_{0}\) 를 제외시키게 되면, 회귀직선은 반드시 원점을 지나가야 하는데, 이것은 지나치게 강력한 제한사항이라고 할 수 있다. 예시 자료를 이용해서 이 문제를 살펴보자. 주어진 자료에 대해 식 (3.1)에 설정된 절편이 포함된 일반적인 단순회귀모형으로 추정된 회귀직선과 원점을 제거한 회귀모형인 \(Y=\beta_{1}X+\varepsilon\) 으로 추정된 회귀직선이 그림 3.4에 표시되어 있다.

주어진 자료에서 가설 \(H_{0}:\beta_{0}=0, ~~H_{1}:\beta_{0} \ne 0\) 에 대한 p-값은 0.248으로 계산되어 \(H_{0}\) 을 기각할 수 없는 상황이다. 두 회귀직선 사이에는 무시할 수 없는 차이가 있는 것으로 보이는데, 절편이 포함된 회귀직선의 경우에는 잔차제곱합이 \(RSS=\) 118.98인 반면에, 절편이 제거되어 원점을 지나는 회귀직선의 경우에는 잔차제곱합이 \(RSS=\) 124.89로 계산된다. 따라서 가설검정의 결과에 따라 절편을 제거한 회귀모형의 적합도가 더 떨어지는 것을 볼 수 있다.

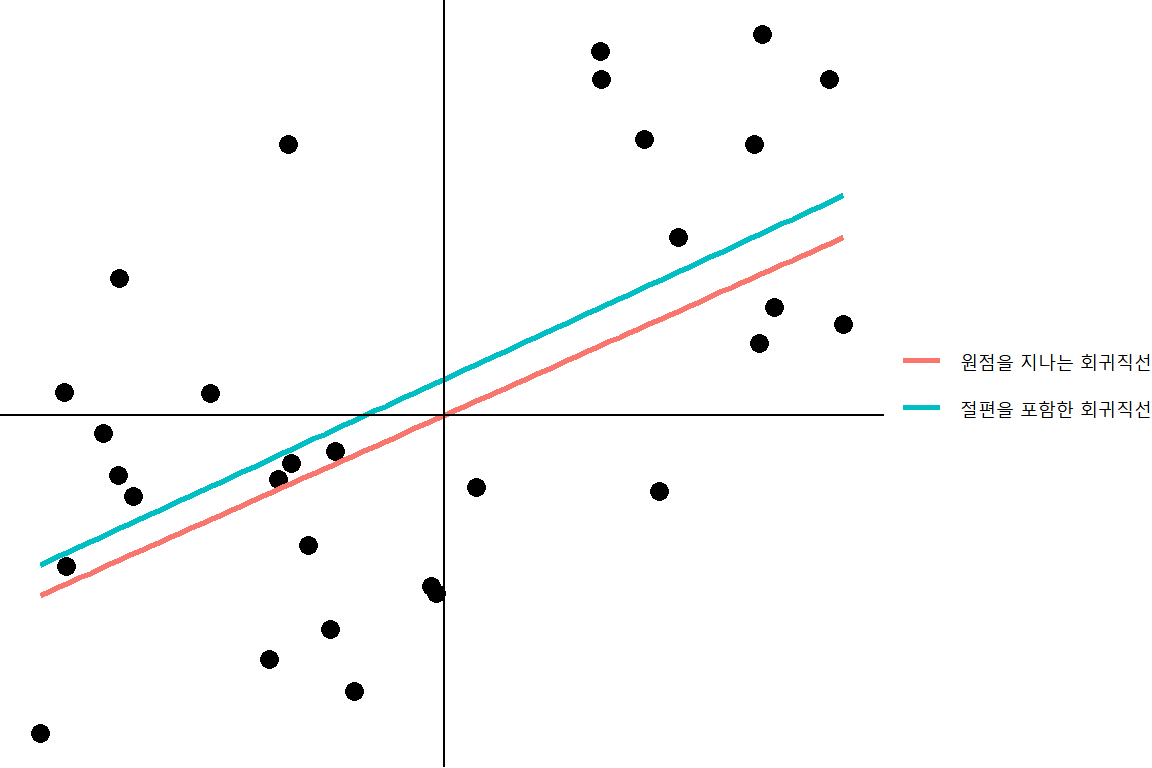
절편을 제거한 회귀모형의 한계

그림 3.4: 절편을 제거한 회귀모형의 한계

\(\bullet\) 예제 3.1: 매출액에 대한 광고효과 회귀모형의 회귀계수에 대한 추론

예제 2.2의 자료 ex2-2.csv에 대하여 다음의 분석을 실시해 보자.

  1. 광고비 지출이 매출액 증가에 양의 효과가 있는지 검정하라.

  2. 기울기 모수인 \(\beta_{1}\)에 대한 95% 신뢰구간을 추정하라.

회귀모형의 적합은 함수 lm()으로 이루어진다. 적합된 회귀모형에 대한 추론을 위해서는 lm()으로 생성된 객체에 다른 함수를 적용시켜 생성된 객체를 대상으로 이루어진다. 추론을 위해 사용되는 가장 대표적인 함수는 summary()이다. 자료 ex2-2.csv를 대상으로 회귀모형을 적합시켜보자.

df2.2 <- readr::read_csv("Data/ex2-2.csv")
fit2.2 <- lm(sales ~ advertisement, data = df2.2)

함수 lm()으로 생성된 객체 fit2.2에 회귀모형의 추론 단계에서 가장 빈번하게 사용되는 함수 summary()를 적용시킨 결과를 확인해 보자.

summary(fit2.2)
## 
## Call:
## lm(formula = sales ~ advertisement, data = df2.2)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -158.433  -15.093    0.557   21.674  151.973 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)     -6.944     52.004  -0.134    0.895    
## advertisement   17.713      1.685  10.511 4.13e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 60.41 on 18 degrees of freedom
## Multiple R-squared:  0.8599, Adjusted R-squared:  0.8521 
## F-statistic: 110.5 on 1 and 18 DF,  p-value: 4.126e-09

함수 summary()의 결과물은 SAS나 SPSS에서 볼 수 있는 결과물과는 형식에서 차이가 있으나, 많은 정보를 매우 효율적으로 보여주는 방식이라고 하겠다. 결과물을 하나씩 살펴보자.

먼저 Residuals:에는 잔차의 분포 형태를 엿볼 수 있는 요약통계가 계산되어 있다. 가정이 만족된다면 평균이 0인 정규분포를 보이게 되는데, 잔차의 요약통계 결과로 대략적인 판단을 할 수 있다. 잔차에 대한 분석은 5장에서 살펴볼 것이다.

Coefficients:에는 회귀계수의 추정값이 Estimate에, 표준오차가 Std. Error에 각각 계산되어 있다. 또한 개별 회귀계수의 유의성 검정인 \(H_{0}:\beta_{j} = 0, ~~H_{1}: \beta_{j} \ne 0\) 에 대한 검정통계량의 값이 t value에, p-값이 Pr(>|t|)이 각각 계산되어 있다.

Residual standard error:는 식 (2.17)에서 정의된 \(MSE\) 에 제곱근을 취한 값으로 \(\sigma\) 에 대한 추정 결과이며, 회귀모형의 평가 측도로 사용된다. Multiple R-squared:와 Adjusted R-squared:, 그리고 F-statistic:의 내용은 추후에 살펴보겠다.

이제 예제 문제를 해결해 보자. 광고비 지출이 매출액 증가에 양의 효과가 있는지 여부를 확인하는 것은 식 (3.9)와는 다르게 다음과 같은 단측검정이 된다.

\[\begin{equation} H_{0}:\beta_{1}=0, ~~H_{1}:\beta_{1}>0 \tag{3.14} \end{equation}\]

광고비 지출이 매출액 증가에는 음의 효과가 있을 수 없다는 확신이 있는 경우에만 적용할 수 있는 가설이며, 가설은 반드시 자료를 조사하기 전에 설정되어야 한다.

함수 summary()에서 계산한 p-값은 식 (3.9)의 양측검정에 대한 것으로서, \(P(t > |t_{0}|)\) 을 계산한 것이다. 여기에서 \(t\) 는 자유도가 \((n-2)\) 인 \(t\) 분포이고 \(|t_{0}|\) 는 자료에서 계산된 검정통계량 값을 나타낸다. 식 (3.14)의 단측검정에 대한 p-값은 \(P(t>t_{0})\)가 되는데, 예제 자료에서는 \(t_{0}=\) 17.713으로 양수이므로 함수 summary()에서 계산한 p-값을 2로 나누면 된다. 따라서 양의 효과가 있는지 여부를 확인하는 가설의 p-값은 2.063186e-09 이 되어서, \(H_{0}\) 을 기각하는데 문제가 없어 보인다. 즉, 광고비 지출이 매출액 증가에 양의 효과가 있는 것으로 볼 수 있다.

회귀계수에 대한 신뢰구간은 함수 lm()으로 생성된 객체를 함수 confint()에 적용시키면 얻을 수 있다. 함수 confint()의 기본적인 사용법은 confint(object, level = 0.95)인데, object는 함수 lm()으로 생성된 객체이고, level은 신뢰수준을 지정하는 것으로서 95%가 디폴트 값이다. 이제 광고비 자료에 대한 회귀모형 객체인 fit2.2를 함수 confint()에 적용시킨 결과를 살펴보자.

confint(fit2.2)
##                    2.5 %    97.5 %
## (Intercept)   -116.20070 102.31274
## advertisement   14.17241  21.25336

만일 90% 신뢰구간을 계산하고자 한다면, level = 0.9를 추가하면 된다.

confint(fit2.2, level = 0.9)
##                     5 %     95 %
## (Intercept)   -97.12253 83.23457
## advertisement  14.79064 20.63513

3.3 반응변수의 평균, \(E(Y|X_{o})\)에 대한 신뢰구간 추정

새롭게 관측되는 설명변수 자료에 대한 가장 정확한 반응변수의 예측값을 생성하는 것이 회귀분석의 목적이 되는 경우가 많이 있다. 반응변수의 예측값은 대부분의 경우 반응변수의 평균을 의미하는데, 경우에 따라서는 반응변수의 개별 관측값을 예측하고자 하는 경우도 있을 수 있다. 반응변수의 평균 예측에 대한 문제는 이번 절에서 살펴볼 것이고, 반응변수의 개별 관측값 예측에 대한 문제는 다음 절에서 살펴볼 것이다.

식 (3.1)의 회귀모형에 의하면, 반응변수 \(Y\) 의 평균값은 설명변수의 값에 따라 다른 값을 갖게 된다. 따라서 반응변수의 평균을 예측하고자 하는 설명변수의 수준을 먼저 지정해야 하는데, 이 값을 \(X_{o}\) 라고 하자. 그러면 지정된 설명변수 수준에 대한 반응변수의 평균값은 \(E(Y|X_{o})\) 가 되는데, 이 때 설명변수의 수준 \(X_{o}\) 는 현재 분석에 사용된 자료의 범위 내에서 지정하는 것이 안전하다. 그 이유는 그림 1.5에서 살펴본 회귀모형의 유의성 문제로 인하여, 현재 수집된 자료 범위를 벗어난 영역에 대해서는 가급적 예측을 실시하지 않는 것이 안전하기 때문이다.

\(E(Y|X_{o})=\beta_{0}+\beta_{1}X_{o}\) 에 대한 불편추정량은 \(\beta_{0}\) 와 \(\beta_{1}\) 에 대한 불편추정량을 각각 적용시켜서 다음과 같이 주어진다.

\[\begin{equation} \widehat{E(Y|X_{o})} \equiv \widehat{Y}_{o} = \hat{\beta}_{0} + \hat{\beta}_{1}X_{o} \tag{3.15} \end{equation}\]

\(E(Y|X_{o})\) 에 대한 신뢰구간을 추정하기 위해서는 \(E(Y|X_{o})\) 의 불편추정량인 \(\widehat{Y}_{o}\) 의 표본분포를 유도해야 한다. \(\widehat{Y}_{o}\) 은 \(\hat{\beta}_{0}\) 와 \(\hat{\beta}_{1}\) 의 선형결합으로 이루어져 있는데, \(\hat{\beta}_{0}\) 와 \(\hat{\beta}_{1}\) 은 2.2.2절에서 살펴보았지만 모두 \(Y_{i}\) 의 선형결합으로 표현된다. 따라서 \(\widehat{Y}_{o}\) 은 \(Y_{i}\) 와 동일하게 정규분포를 따르게 된다.

또한 \(\widehat{Y}_{o}\) 의 분산은 다음과 같이 유도할 수 있다.

\[\begin{align} Var(\widehat{Y}_{o}) &= Var(\hat{\beta}_{0}+\hat{\beta}_{1}X_{o}) \\ &= Var(\overline{Y}-\hat{\beta}_{1}\overline{X}+\hat{\beta}_{1}X_{O}) \\ &= Var(\overline{Y}+\hat{\beta}_{1}(X_{o}-\overline{X})) \\ &= \frac{\sigma^{2}}{n}+\frac{(X_{o}-\overline{X})^{2}\cdot \sigma^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}} \\ &= \sigma^{2}\left(\frac{1}{n}+\frac{(X_{o}-\overline{X})^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right) \tag{3.16} \end{align}\]

식 (3.16)의 세 번째에서 네 번째 단계로 넘어오는 과정에는 \(Cov(\overline{Y}, \hat{\beta}_{1})=0\) 이 필요한데, 이것의 증명은 2장 연습문제로 주어졌다.

따라서 \(\widehat{Y}_{o}\) 의 표본분포는 다음과 같다.

\[\begin{equation} \widehat{Y}_{o} \sim N\left(\beta_{0}+\beta_{1}X_{o},~\sigma^{2}\left(\frac{1}{n}+\frac{(X_{o}-\overline{X})^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right) \right) \end{equation}\]

\(E(Y|X_{o})\) 의 불편추정량인 \(\widehat{Y}_{o}\) 을 표준화시킨 통계량 \(t\) 는 다음과 같이 표현되며, 분포는 \(\hat{\beta}_{1}\)의 경우와 동일하게 \(t(n-2)\) 가 된다.

\[\begin{equation} t = \frac{\widehat{Y}_{o}-E(Y|X_{o})}{\sqrt{MSE\left(\frac{1}{n}+\frac{(X_{o}-\overline{X})^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right)}} \tag{3.17} \end{equation}\]

모수 \(E(Y|X_{o})\) 의 \(100 \times (1-\alpha)\)% 신뢰구간은 식 (3.17)을 이용하면 다음과 같이 유도된다.

\[\begin{align} 1-\alpha &= P\left(-t_{\alpha, n-2}<\frac{\widehat{Y}_{o}-E(Y|X_{o})}{SE(\widehat{Y}_{o})}<t_{\alpha, n-2} \right) \\ &= P\left(\widehat{Y}_{o}-t_{\alpha, n-2}\cdot SE(\widehat{Y}_{o}) < E(Y|X_{o}) < \widehat{Y}_{o}+t_{\alpha, n-2}\cdot SE(\widehat{Y}_{o})\right) \tag{3.18} \end{align}\]

단, \(SE(\widehat{Y}_{o})) = \sqrt{MSE\left(\frac{1}{n}+\frac{(X_{o}-\overline{X})^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right)}\) 을 나타내며, \(t_{\alpha, n-2}\) 는 자유도가 \((n-2)\) 인 \(t\) 분포의 상위 \(100 \times \alpha\) 백분위수를 나타낸다.

식 (3.18)의 신뢰구간에서 확인할 수 있는 것은 신뢰구간의 폭이 \(X_{o} = \overline{X}\) 일 때 최소가 되며, \(|X_{o}-\overline{X}|\) 의 값이 증가함에 따라 점점 넓어진다는 점이다. 즉, \(E(Y|X_{o})\) 에 대한 추정은 \(X_{o}\) 의 값이 자료의 평균에 가까우면 좋은 결과를 기대할 수 있지만, 그렇지 않은 경우에는 신뢰도가 많이 떨어질 수 있다는 것을 의미한다.

3.4 반응변수의 개별 관측값 예측

이번 절에서는 주어진 설명변수의 수준에 대한 반응변수의 개별 관측값 예측에 대한 문제를 살펴보겠다. 이번 절에서도 미리 지정되는 설명변수의 수준을 \(X_{o}\) 라고 하고, \(X_{o}\) 에 해당하는 새로운 관측값을 \(Y_{o}\) 라고 하자. 새로운 관측값 \(Y_{o}\) 는 식 (3.1)의 회귀모형에 의해서 다음과 같이 주어진다.

\[\begin{equation} Y_{o} = \beta_{0} + \beta_{1}X_{o} + \varepsilon_{o} \end{equation}\]

\(Y_{o}\) 의 점추정량 \(\widehat{Y}_{o}\) 을 구하기 위해서는 \(\beta_{0}\) 와 \(\beta_{1}\) 을 각각의 불편추정량으로 대체하고, 확률변수인 \(\varepsilon_{o}\) 은 \(N(0,\sigma^{2})\) 에 따른 임의의 값을 갖게 되기 때문에 정확한 값을 예측할 수 없는 대상이어서 평균값 0으로 적용시켜서 다음과 같이 구할 수 있다.

\[\begin{equation} \widehat{Y}_{o} = \hat{\beta}_{0} + \hat{\beta}_{1}X_{o} \tag{3.19} \end{equation}\]

따라서 개별 관측값 \(Y_{o}\) 와 평균 관측값 \(E(Y|X_{o})\) 는 식 (3.15)와 (3.19)에 주어진 동일한 점추정량 \(\widehat{Y}_{o}\) 을 갖게 된다.

\(Y_{o}\) 에 대한 예측구간을 추정하기 위해 다음의 확률변수를 고려해 보자.

\[\begin{equation} \psi = \widehat{Y}_{o}-Y_{o} \end{equation}\]

확률변수 \(\psi\) 는 \(Y_{i}\) 와 동일한 분포를 하기 때문에 정규분포를 따르고 있으며, 평균은 다음과 같고, \[\begin{align*} E(\psi) &= E(\widehat{Y}_{o}-Y_{o}) \\ &= E(\hat{\beta}_{o}+\hat{\beta}_{1}X_{o}) - E(\beta_{0} + \beta_{1}X_{o} + \varepsilon_{o}) \\ &= 0 \end{align*}\]

분산은 다음과 같이 유도된다.

\[\begin{align*} Var(\psi) &= Var(\widehat{Y}_{o}-Y_{o}) \\ &= Var(\widehat{Y}_{o}) + Var(Y_{o}) \\ &= \sigma^{2}\left(\frac{1}{n}+\frac{(X_{o}-\overline{X})^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right) + \sigma^{2} \\ & = \sigma^{2}\left(1+\frac{1}{n}+\frac{(X_{o}-\overline{X})^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right) \end{align*}\]

확률변수 \(\psi\) 를 표준화시킨 통계량 \(t\) 는 다음과 같이 표현되며, 분포는 \(t(n-2)\) 가 된다.

\[\begin{equation} t = \frac{\widehat{Y}_{o}-Y_{o}}{SE(\psi)} \end{equation}\]

단, \(SE(\psi) = \sqrt{MSE\left(1+\frac{1}{n}+\frac{(X_{o}-\overline{X})^{2}}{\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}\right)}\).

따라서 미리 지정되는 설명변수의 수준 \(X_{o}\) 에 대해 새롭게 관측될 개별 반응변수 값 \(Y_{o}\) 의 \(100 \times (1-\alpha)\)% 예측구간은 다음과 같이 주어진다.

\[\begin{align*} 1-\alpha &= P\left(-t_{\alpha, n-2}<\frac{\widehat{Y}_{o}-Y_{o}}{SE(\psi)}<t_{\alpha, n-2} \right) \\ &= P\left(\widehat{Y}_{o}-t_{\alpha, n-2}\cdot SE(\psi) < Y_{o} < \widehat{Y}_{o}+t_{\alpha, n-2}\cdot SE(\psi)\right) \tag{3.20} \end{align*}\]

지정된 설명변수 수준 \(X_{o}\) 에 대한 반응변수의 평균에 대한 신뢰구간과 반응변수의 개별 관측값에 대한 예측구간의 폭을 비교해 보면, 식 (3.20)의 예측구간이 식 (3.18)의 신뢰구간보다 항상 더 넓다는 것을 알 수 있다. 이것은 예측구간이 \(E(Y|X_{o})\) 을 \(\widehat{Y}_{o}\) 으로 추정하는 과정에서 발생하는 오차와 새로운 관측값 \(Y_{o}\) 에 의해 발생하는 오차를 모두 포함하기 때문이다.

\(\bullet\) 예제 3.2: 매출액에 대한 광고효과 회귀모형에서 매출액의 신뢰구간과 예측구간 추정

예제 2.2 자료 ex2-2.csv에 대하여 다음의 분석을 실시해 보자.

  1. 모형 적합에 사용된 광고비 자료에 대한 평균 매출액의 95% 신뢰구간과 매출액의 개별 관측값에 대한 95% 예측구간을 구하라.

  2. 피자 체인점들이 광고비를 25, 30, 35, 40을 각각 지출하면 얻게 될 것으로 예상되는 매출액의 평균은 어떻게 되는가? 평균 매출액에 대한 95% 신뢰구간을 구하라.

  3. 수원에 있는 어느 특정 피자 체인점이 광고비를 25, 30, 35, 40을 각각 지출하면 얻게 될 것으로 예측되는 매출액의 95% 예측구간을 구하라.

적합된 회귀모형의 예측에 사용되는 함수는 predict()이다. 함수 lm()으로 생성된 회귀모형 객체에 대한 predict()의 기본적인 사용법은 다음과 같다.

predict(object, newdata, interval = c("none", "confidence", "prediction"))

object는 함수 lm()으로 생성된 객체이고, newdata는 새롭게 주어지는 설명변수의 값으로 반드시 데이터 프레임으로 입력되어야 하며, 생략이 되면 모형적합에 사용된 자료에 대한 예측이 이루어진다. interval은 구간의 종류를 선택하는 것으로서, 평균 반응변수에 대한 신뢰구간은 "confidence", 반응변수의 개별 관측값에 대한 예측구간은 "prediction"을 선택하면 되고, 신뢰구간을 원하지 않는 경우에는 "none"을 선택하면 된다. 디폴트는 "none"이다.

자료 ex2-2.csv에 대하여 회귀모형 객체 fit2.2를 생성하자.

df2.2 <- read_csv("Data/ex2-2.csv")
fit2.2 <- lm(sales ~ advertisement, data = df2.2)

예제의 첫 번째 문제는 모형적합에 사용된 광고비 자료에 대한 예측이다. 따라서 함수 predict()에 newdata를 지정하지 않고 interval을 "confidence"와 "prediction"을 각각 지정해서 평균 반응변수에 대한 신뢰구간과 개별 관측값에 대한 예측구간을 구하면 된다.

pred_1 <- predict(fit2.2, interval = "confidence")
pred_2 <- predict(fit2.2, interval = "prediction")

두 구간의 폭은 그래프로 비교해 보자.

library(patchwork)
p1 <- cbind(df2.2, pred_1) |> 
  ggplot(aes(x = advertisement, y = sales)) +
  geom_point() +
  geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.1, fill = "pink",
              color = "red", linewidth = 1) +
  ggtitle("반응변수 평균에 대한 신뢰구간")

p2 <- cbind(df2.2, pred_2) |> 
  ggplot(aes(x = advertisement, y = sales)) +
  geom_point() +
  geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.1, fill = "skyblue",
              color = "blue", linewidth = 1) +
  ggtitle("반응변수 개별 관측값에 대한 예측구간")

p1 + p2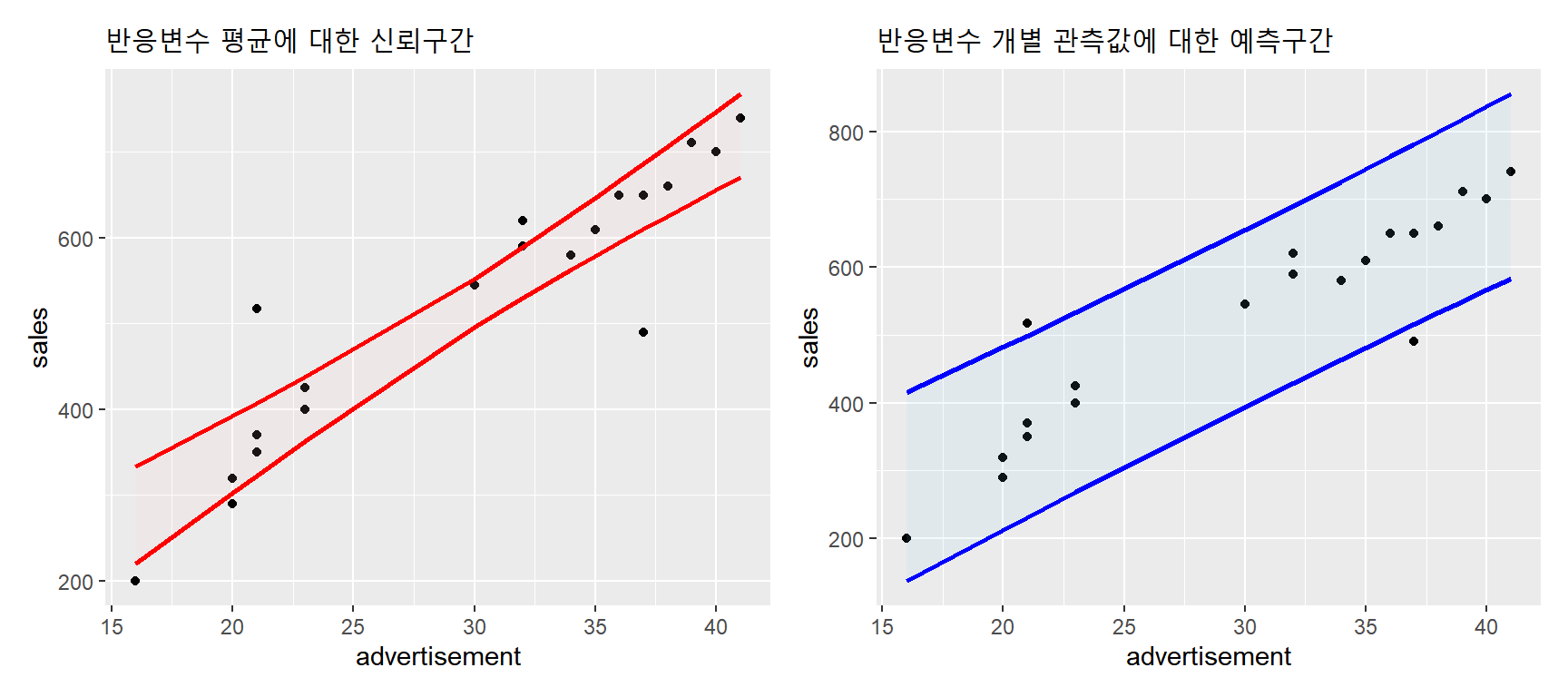
매출액 자료에 대한 신뢰구간과 예측구간 비교

그림 3.5: 매출액 자료에 대한 신뢰구간과 예측구간 비교

예제의 두 번째와 세 번째 문제는 새롭게 주어진 설명변수 값에 대하여 평균 매출액에 대한 신뢰구간과 개별 관측값에 대한 예측구간을 추정하는 문제이다. 새롭게 주어진 설명변수 값을 데이터 프레임으로 지정하고, 예측을 실시해 보자.

new_data <- data.frame(advertisement = c(25, 30, 35, 40))
pred_3 <- predict(fit2.2, newdata = new_data, interval = "confidence")
pred_4 <- predict(fit2.2, newdata = new_data, interval = "prediction")

신뢰구간의 폭은 새롭게 주어지는 설명변수의 값이 자료의 평균인 29.8에 가까울수록 작아진다.

new_data |> cbind(pred_3) |> mutate(width = upr - lwr)
##   advertisement      fit      lwr      upr    width
## 1            25 435.8782 402.7979 468.9584 66.16044
## 2            30 524.4426 496.0525 552.8327 56.78018
## 3            35 613.0070 579.1774 646.8366 67.65917
## 4            40 701.5714 655.6407 747.5022 91.86146

예측구간은 폭도 신뢰구간의 경우와 동일하게 자료의 평균에 가까울수록 작아지지만, 이 예제의 경우에는 상대적으로 큰 차이가 없는 것을 알 수 있다.

new_data |> cbind(pred_4) |> mutate(width = upr - lwr)
##   advertisement      fit      lwr      upr    width
## 1            25 435.8782 304.7133 567.0430 262.3297
## 2            30 524.4426 394.3814 654.5038 260.1224
## 3            35 613.0070 481.6512 744.3628 262.7117
## 4            40 701.5714 566.5916 836.5512 269.9596

3.5 상관계수 : 두 변수 사이의 선형 연관성 측정

두 변수 사이의 선형 관련성을 측정하는 통계량으로 식 (2.2)에 정의된 공분산이 있다. 공분산의 값이 크면 두 변수 사이에 강한 양의 관계 또는 음의 관계가 있다고 할 수 있지만, 값이 작으면 선형 관계가 명확하지 않다고 할 수 있다. 그러나 공분산은 변수가 취하는 값 자체의 절대적 크기에도 영향을 받는 통계량이기 때문에, ‘값이 크다’ 또는 ’값이 작다’에 대한 절대적 기준을 제시할 수 없는데, 이 문제는 두 변수의 표준편차를 나누어 값을 상대화시킴으로서 해결할 수 있다. 이것이 두 변수의 상관계수 \(\rho\) 가 된다.

\[\begin{equation} \rho = \frac{Cov(Y,X)}{\sqrt{Var(Y)}\sqrt{Var(X)}} \tag{3.21} \end{equation}\]

상관계수는 \(-1 \leq \rho \leq 1\) 의 범위를 취하고 있는데, \(1\)과 \(-1\)이 되면 두 변수가 완벽한 선형관계를 갖게 되고, \(0\)에 가까울수록 명확한 선형관계가 없는 경우가 된다. 그림 3.6은 상관관계의 값에 따라 두 변수의 산점도에 어떤 변화가 생길 수 있는지를 보여주는 모의자료에 대한 산점도이다.

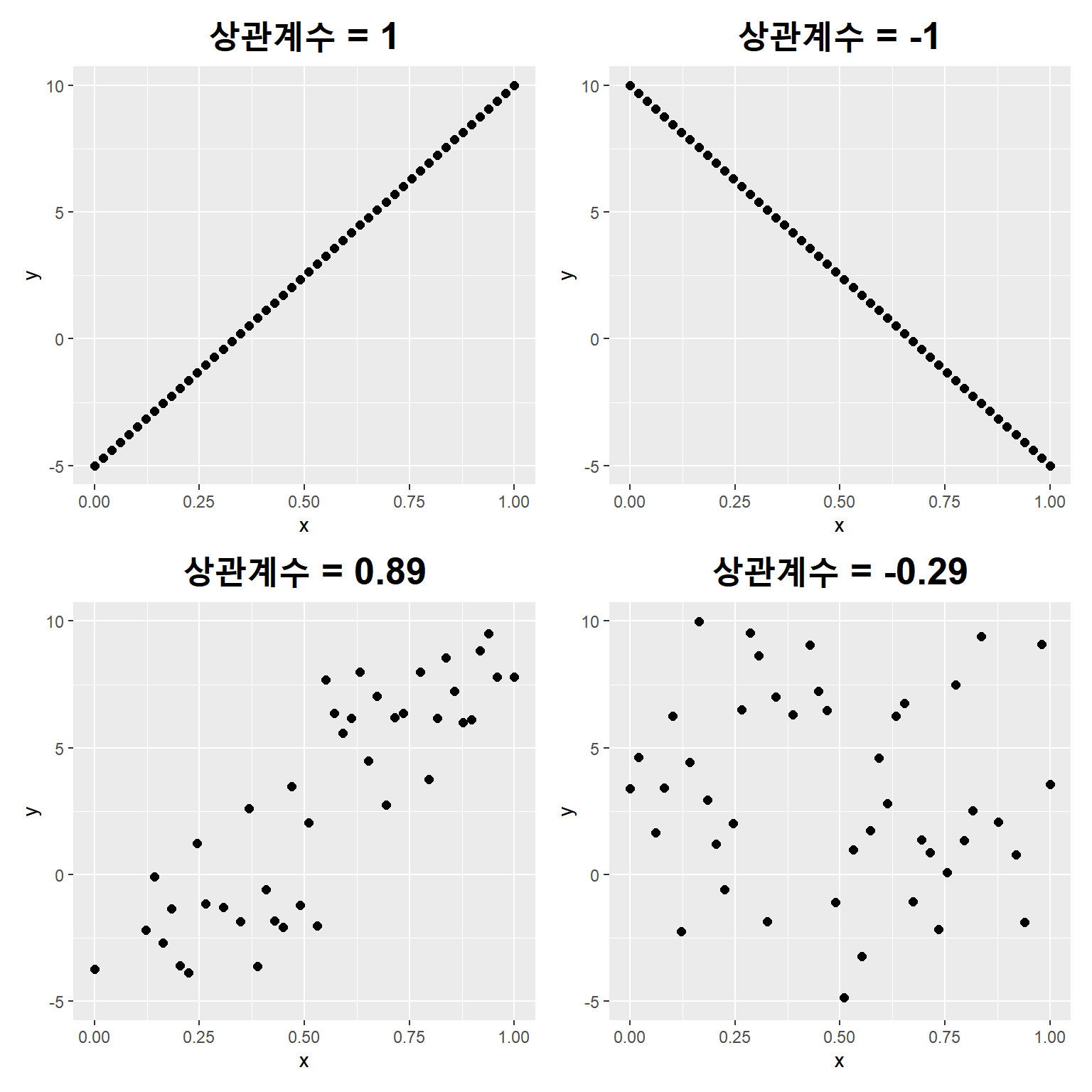
상관계수와 두 변수 산점도 형태

그림 3.6: 상관계수와 두 변수 산점도 형태

공분산이나 상관계수는 두 변수가 모두 확률변수인 경우에 적용되는 개념이다. 그러나 식 (2.1)에서 설정한 회귀모형에서 설명변수 \(X\) 는 분석자가 통제할 수 있는 변량이고, 반응변수만 확률변수라고 가정하였다. 하지만 설명변수 \(X\) 의 수준을 분석자가 임의로 조절하는 것이 불가능한 경우가 많이 있으며, 이런 상황에서는 변수 \(Y\) 와 \(X\) 가 모두 확률변수가 된다.

예를 들어 그림 1.1에서 다루고 있는 일일 최고 기온과 전기 사용량의 관계에서 설명변수인 일일 최고 기온의 수준은 분석자가 임의로 선택할 수 없는 변량이 된다. 또한 예제 2.2에서 다루고 있는 매출액에 대한 광고비 효과 자료에서도 실제로 우리는 피자 체인점을 임의로 선택해서 지출된 광고비와 매출액을 관측하는 것이기 때문에 광고비 수준을 분석자가 미리 설정하는 것은 어려운 상황이라고 할 수 있다.

이와 같이 설명변수도 확률변수인 경우에는 관측된 설명변수의 수준을 조건부로 하여 회귀모형에 대한 추론을 실시하게 된다.

식 (3.21)에 주어진 모수 \(\rho\) 는 다음의 표본 상관계수로 추정할 수 있다.

\[\begin{equation} r = \frac{\sum_{i=1}^{n} (X_{i}-\overline{X})(Y_{i}-\overline{Y})}{\sqrt{\sum_{i=1}^{n} (X_{i}-\overline{X})^{2}}\sqrt{\sum_{i=1}^{n}(Y_{i}-\overline{Y})^{2}}} \tag{3.22} \end{equation}\]

상관계수의 유의성 검정은 다음의 가설에 대한 검정이다.

\[\begin{equation} H_{0}: \rho = 0,~~H_{1}:\rho \ne 0 \end{equation}\]

검정통계량 \(t\) 는 다음과 같이 주어지며, \(H_{0}\) 이 사실인 경우의 분포는 \(t(n-2)\) 가 된다.

\[\begin{equation} t = \frac{r \sqrt{n-2}}{\sqrt{1-r^{2}}} \end{equation}\]

상관계수의 유의성 검정으로 \(H_{0}\) 이 기각되면, 두 변수 사이에 유의한 선형관계가 있다는 것을 의미한다. 하지만 그렇다고 해서 두 변수 사이에 강한 선형관계가 있다는 것을 의미하는 것은 아니다. 그림 3.6에서 상관계수 값이 -0.29인 자료의 산점도를 보면 두 변수 사이에는 마치 선형관계가 없는 것으로 보인다. 하지만 상관계수의 유의성 검정을 실시하면 조금 다른 결과를 얻게 되는데, 상관계수의 유의성 검정은 함수 cor.test()로 할 수 있다.

cor.test(x,y)
## 
##  Pearson's product-moment correlation
## 
## data:  x and y
## t = -2.0846, df = 48, p-value = 0.04245
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.52441468 -0.01062909
## sample estimates:
##        cor 
## -0.2881244

검정 결과는 두 변수 사이에 유의한 선형관계가 존재하는 것으로 나왔다.

3.6 연습문제

1. 단순회귀모형에서 기울기 모수인 \(\beta_{1}\) 에 대한 다음의 가설 검정을 실시하고자 한다.

\[\begin{equation} H_{0}: \beta_{1}=0,~~H_{1}: \beta_{1} \ne 0 \end{equation}\]

  • 검정통계량을 정의하고, 유도되는 과정을 설명하라.

  • \(H_{0}\) 이 사실인 경우, 검정통계량의 분포는 무엇인가? 이 분포가 검정 과정에서 어떤 역할을 하고 있는지 설명하라.

2. 데이터 프레임 mtcars의 변수 mpg를 반응변수로, disp를 설명변수로 하는 회귀모형을 함수 lm()으로 적합시키고, 그 결과를 함수 summary()에 입력한 결과가 다음과 같다. 분석 목적은 자동차 엔진 배기량(disp)이 증가하면 연비(mpg)가 떨어진다는 가설을 검정하는 것이다.

lm(mpg ~ disp, data = mtcars) |> summary()
## 
## Call:
## lm(formula = mpg ~ disp, data = mtcars)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.8922 -2.2022 -0.9631  1.6272  7.2305 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 29.599855   1.229720  24.070  < 2e-16 ***
## disp        -0.041215   0.004712  -8.747 9.38e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.251 on 30 degrees of freedom
## Multiple R-squared:  0.7183, Adjusted R-squared:  0.709 
## F-statistic: 76.51 on 1 and 30 DF,  p-value: 9.38e-10

  • 추정된 회귀모형식을 작성하고, 그 의미를 해석하라.

  • 분석 목적을 위한 가설을 작성하라.

  • 검정통계량의 값은 무엇이며, 어떻게 계산되었는지 설명하라.

  • p-value를 계산하고, 가설 검정을 실시하라. 가설 검정 결과에서는 어떤 오류가 발생할 수 있는가?

3. 두 변수 사이의 선형 관련성을 측정하고자 한다.

  • 두 변수의 공분산은 무엇이며, 어떻게 두 변수 사이의 선형 관련성을 측정할 수 있는가?

  • 두 변수 사이의 선형 관련성은 공분산이 아닌 상관계수로 측정하는 것이 일반적이다. 그 이유는 무엇인가?

4. 단순회귀모형 \(Y=\beta_{0}+\beta_{1}X+\varepsilon\) 에서 기울기 모수 \(\beta_{1}\) 에 대한 유의성 검정과 두 변수 \((X,Y)\) 의 상관계수에 대한 유의성 검정에는 어떤 관련성이 있는지 설명하라.

5. 자동차의 특정 주행속도(speed)에서 급제동을 해서 차를 완전히 멈추는데 필요한 거리(dist)를 측정하는 실험을 50회 반복한 자료의 산점도이다. speed의 단위는 mph이고, dist의 단위는 feet이다.

cars |> 
  ggplot(aes(x = speed, y = dist)) +
  geom_point()

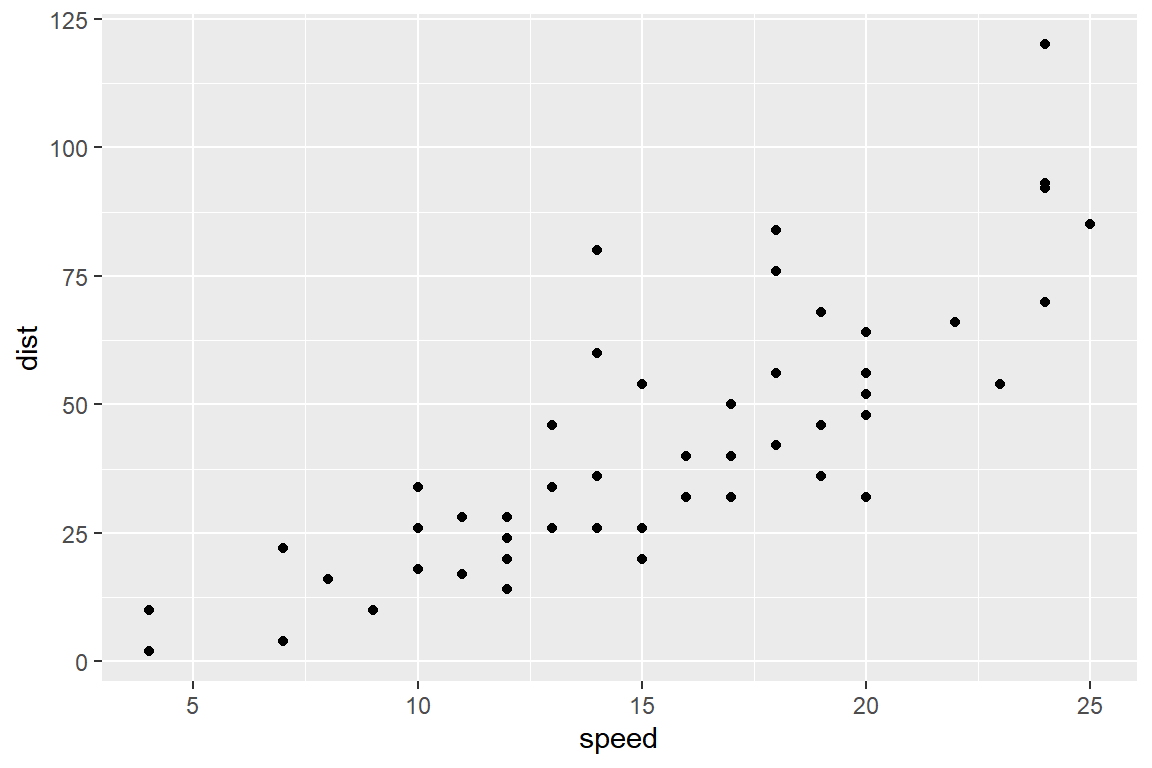
speed를 설명변수로 하는 dist에 대한 단순회귀모형을 적합한 결과가 다음과 같다.

lm(dist ~ speed, cars) |> summary()
## 
## Call:
## lm(formula = dist ~ speed, data = cars)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -29.069  -9.525  -2.272   9.215  43.201 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -17.5791     6.7584  -2.601   0.0123 *  
## speed         3.9324     0.4155   9.464 1.49e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 15.38 on 48 degrees of freedom
## Multiple R-squared:  0.6511, Adjusted R-squared:  0.6438 
## F-statistic: 89.57 on 1 and 48 DF,  p-value: 1.49e-12

  • 추정된 회귀모형식을 작성하고, 의미를 해석하라.

  • 주어진 결과물을 근거로 기울기 모수 \(\beta_{1}\) 에 대한 95% 신뢰구간을 작성하고 해석하라.

  • 자동차의 주행속도가 증가하면 차를 완전히 멈추는데 필요한 거리도 증가한다는 가설을 검정하라.

  • 운행속도가 21mph인 차량을 장애물 60 feet 앞에서 급제동을 했을 때, 장애물과 출동하지 않고 차량을 멈출 수 있겠는가?