5 장 회귀모형의 진단

4.3절에서 우리는 변수선택 과정을 통해 최적모형을 찾는 방법을 살펴보았다. 이제 선택된 모형을 이용하여 반응변수에 대한 예측을 실시하거나 혹은 변수들에 대한 추론 등을 실시할 수 있게 되었다. 그러나 만일 선택된 모형이 회귀모형의 가정을 전혀 만족시키지 못하고 있거나, 혹은 몇몇 극단적인 관찰값으로 인하여 적합 결과가 왜곡되어 있다면 이러한 예측이나 추론 등은 통계적 신빙성이 전혀 없는 결과가 될 수도 있다.

따라서 선택된 회귀모형이 가정사항을 만족하고 있는지를 확인하는 과정이 필요한데, 이것을 회귀진단이라고 한다. 회귀진단은 일반적으로 회귀모형에 대한 진단과 관찰값에 대한 진단으로 구분해서 진행된다.

회귀모형에 대한 진단은 적합된 회귀모형이 중요한 가정 사항을 만족하고 있는지 여부를 확인하는 것으로서, 적합 및 추론의 신빙성을 확보하기 위한 단계가 된다. 관찰값에 대한 진단은 개별 관찰값들이 모형의 적합 과정에 미치는 영향력을 파악해서, 지나치게 큰 영향력을 지닌 관찰값을 확인하기 위한 단계이다.

5.1 회귀모형에 대한 진단

다중회귀모형 \(y_{i}=\beta_{0}+\beta_{1}x_{1i}+\cdots+\beta_{ki}x_{ki}+\varepsilon_{i}\), \(i=1,\ldots,n\) 에 대한 가정은 다음과 같다.

오차항 \(\varepsilon_{1}, \varepsilon_{2}, \cdots, \varepsilon_{n}\) 의 평균은 0, 분산은 \(\sigma^{2}\)
오차항 \(\varepsilon_{1}, \varepsilon_{2}, \cdots, \varepsilon_{n}\) 의 분포는 정규분포
오차항 \(\varepsilon_{1}, \varepsilon_{2}, \cdots, \varepsilon_{n}\) 은 서로 독립
반응변수와 설명변수의 관계는 선형

오차항에 대한 가정 사항이 있지만, 실제 오차항은 관측할 수 없는 대상이기 때문에 만족 여부를 확인할 수 없다. 따라서 오차항에 대한 가정 사항은 잔차 (\(e_{i}=y_{i}-\hat{y}_{i}\))를 이용하여 확인하게 되며, 만족 여부는 대부분 그래프를 이용해서 이루어진다.

4장에서 사용한 예제 자료인 state.x77과 mtcars를 대상으로 회귀모형 진단을 실시해 보자.

\(\bullet\) 예제 : state.x77

state.x77 자료에 대해 4.1.1절에서 이루어진 주된 분석은 다음과 같다.

library(tidyverse)

states <- as.data.frame(state.x77) |>
  rename(Life_Exp = 'Life Exp', HS_Grad = 'HS Grad')

states 자료에 대하여 변수선택 과정 없이 모든 설명변수를 포함한 회귀모형을 적합하고, 그 모형에 대한 회귀진단을 실시해 보자.

fit_s <- lm(Murder ~ ., states)

추정된 회귀모형의 가정 만족 여부를 확인하는 가장 기본적인 절차는 함수 lm()으로 생성된 객체를 함수 plot()에 입력하는 것인데, 네 종류의 그래프가 차례로 그려진다. 작성된 그래프를 하나의 Plots 창에서 함께 보는 것이 편리한데, 그것을 위해서는 함수 par()를 함께 사용해야 한다. 함수 par()는 plot()과 같은 base graphic 함수로 작성된 그래프의 다양한 환경 모수를 조정하는 기능이 있다.

par(mfrow = c(2, 2))
plot(fit_s, pch = 20)
par(mfrow = c(1, 1))

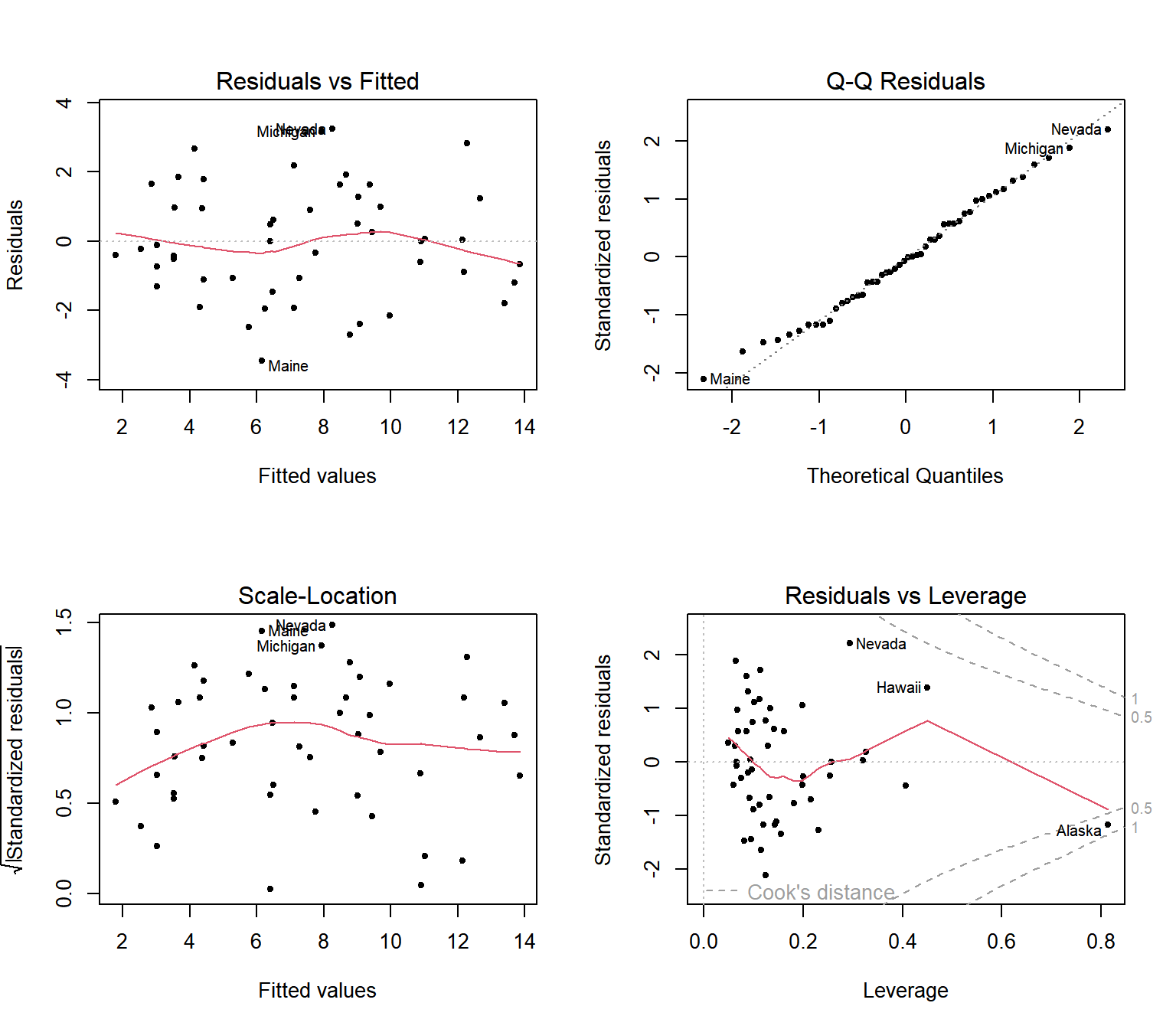
그림 5.1: states 자료에 대한 회귀모형 fit_s의 회귀진단

par(mfrow = c(2, 2))는 Plots 창의 영역을 2개의 행과 2개의 열로 분리시키고, 이어서 작성되는 그래프를 행 단위로 출력하게 한다. plot(fit_s, pch = 20)로 네 종류의 진단 그래프를 작성하고, par(mfrow = c(1, 1))를 실행시켜서 분리된 Plots 창의 영역을 통합하였다. 함수 plot()에 입력한 pch = 20는 점의 모양을 속이 찬 동그란 원으로 지정하기 위해 사용했다.

그림 5.1의 왼쪽 위 패널에 있는 Residuals vs Fitted라는 제목의 그래프는 일반적으로 가장 많이 사용되는 잔차 산점도 그래프로서, 잔차 \(e_{i}\) 와 \(\hat{y}_{i}\) 의 산점도이다. 오른쪽 위 패널에 있는 Q-Q Residuals라는 제목의 그래프는 표준화잔차 \(r_{i}\) 의 정규 분위수-분위수 그래프이다. 왼쪽 아래 패널에 있는 Scale-Location이라는 제목의 그래프는 \(\sqrt{|r_{i}|}\) 와 \(\hat{y}_{i}\) 의 산점도로서 동일 분산 가정의 만족 여부를 확인하는 그래프이다. 마지막으로 오른쪽 아래 패널에 있는 Residuals vs Leverage라는 제목의 그래프는 관찰값의 진단에 사용되는 그래프인데, 관련 통계량 및 그래프에 대한 자세한 설명은 5.2절에서 하겠다.

또한 각 그래프에는 3개의 점 옆에 라벨이 표시되어 있는데, 이것은 각 그래프에서 가장 극단적인 세 점의 행 이름이 표시된 것이다.

Q-Q Residuals 그래프와 Scale-Location 그래프에서 사용된 표준화 잔차는 일반 잔차의 퍼짐 정도를 조정한 잔차로써 다음과 같이 정의된다.

\[\begin{equation} r_{i} = \frac{e_{i}}{RSE \sqrt{1-h_{i}}} \end{equation}\]

회귀모형 fit_s에 대한 잔차와 표준화 잔차의 산점도를 비교해 보자.

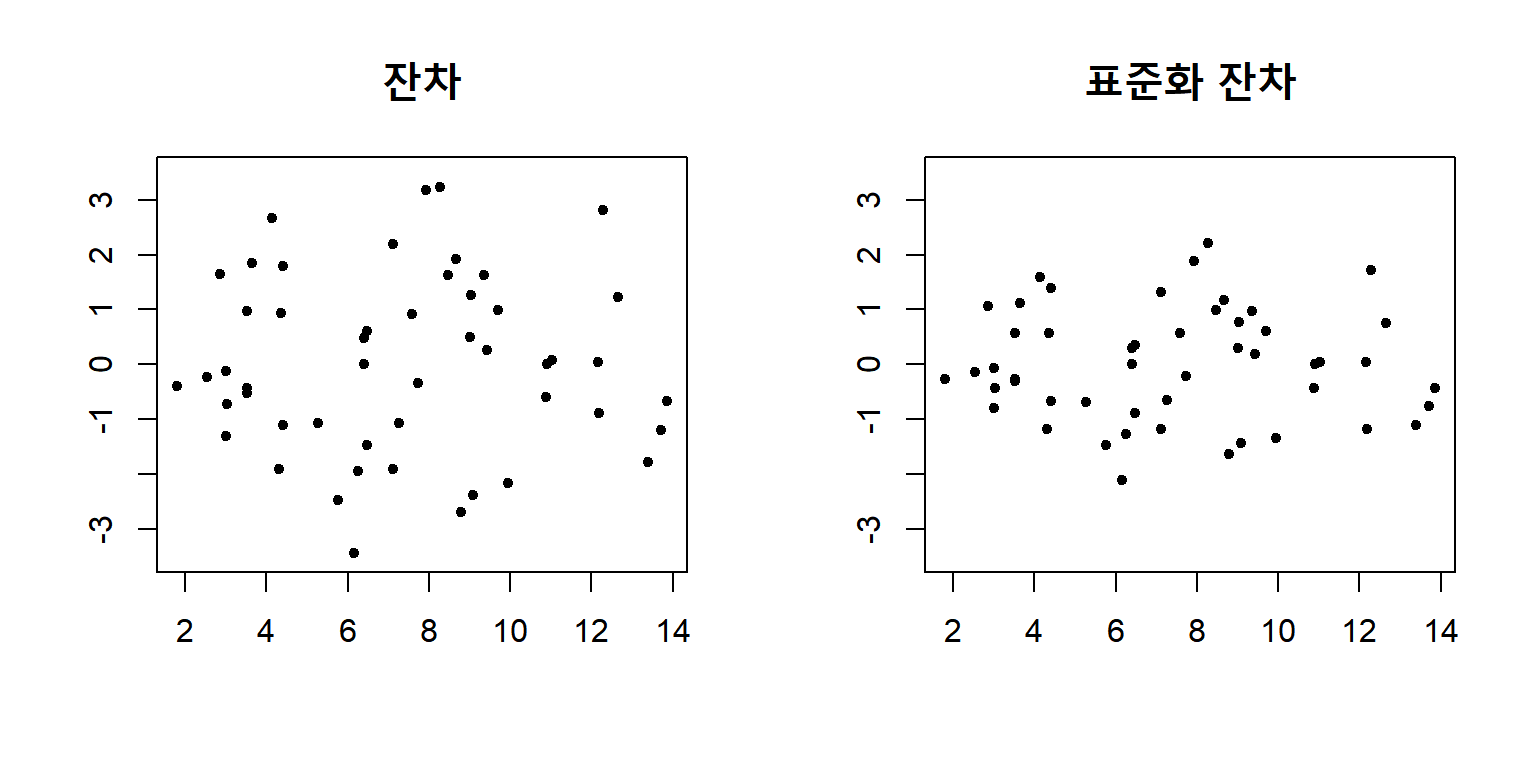
그림 5.2: 모형 fit_s의 잔차와 표준화 잔차의 비교

표준화 잔차를 정의하는데 사용된 \(h_{i}\)는 leverage라고 불리는 통계량으로서, 설명변수들의 \(k\) 차원 공간에서 설명변수의 \(i\) 번째 관찰값이 자료의 중심으로부터 떨어져 있는 거리를 표현하는 것으로 볼 수 있다.

단순회귀모형의 경우 \(i\) 번째 관찰값의 leverage \(h_{i}\) 는 다음과 같이 정의된다.

\[\begin{equation} h_{i} = \frac{1}{n} + \frac{(x_{i}-\overline{x})^{2}}{\sum_{j=1}^{n}(x_{j}-\overline{x})^{2}} \end{equation}\]

Leverage 값이 큰 관찰값은 회귀계수의 추정 결과에 큰 영향을 줄 가능성이 높다고 할 수 있다. 그림 5.3는 leverage가 큰 관찰값이 회귀계수 추정 결과에 어떻게 영향을 줄 수 있는지를 보여주는 모의자료를 이용한 예가 된다. 두 그래프에서 빨간 점은 leverage가 높은 관찰값인데, 실선은 빨간 점을 포함하고 추정한 회귀직선이고, 점선은 빨간 점을 제외한 상테에서 추정한 회귀직선이다. 첫 번째 그래프에서만 큰 영향력을 확인할 수 있다.

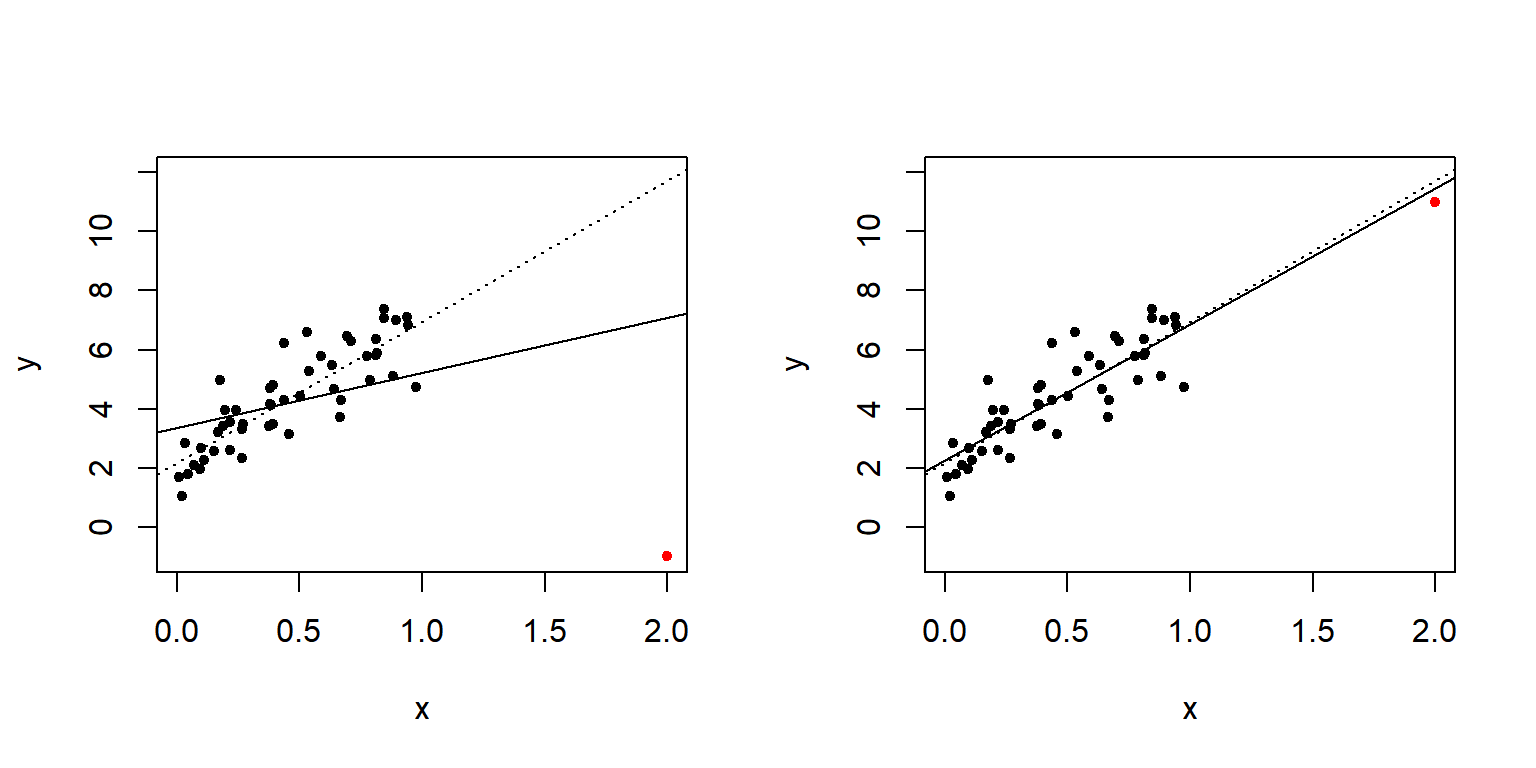
그림 5.3: leverage가 높은 관찰값의 영향력을 보여주는 모의자료

\(\bullet\) 오차항의 동일분산 가정

동일분산 가정의 만족 여부를 확인하는 기본적인 방법은 함수 plot()으로 생성되는 잔차 \(e_{i}\) 와 \(\hat{y}_{i}\) 의 산점도와 \(\sqrt{|r_{i}|}\) 와 \(\hat{y}_{i}\) 의 산점도를 확인하는 것이다. 모형 fit_s에 대한 두 종류의 잔차 산점도를 다시 살펴보자.

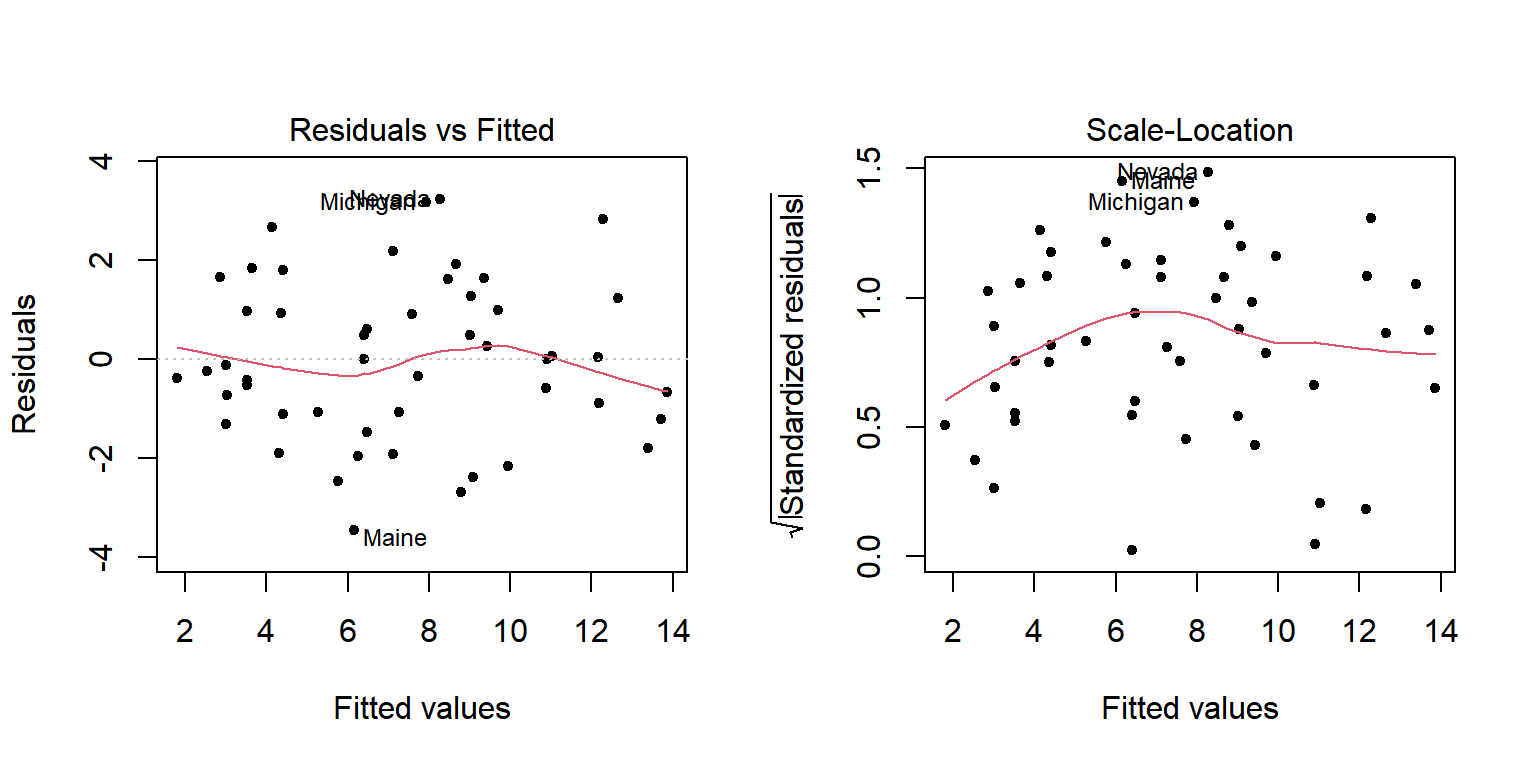
그림 5.4: 동일분산 가정 확인을 위한 잔차 산점도

그림 5.4의 첫 번째 그래프에서는 Y축이 0인 수평선을 중심으로 점들이 거의 일정한 폭을 유지하며 분포하고 있는지 확인해야 한다. 그림 5.4의 두 번째 그래프에서는 점들이 전체적으로 증가하거나 감소하는 패턴이 있는지 확인해야 한다. 그래프에 추가된 빨간 곡선을 참조하여 판단하는 것이 좋은데, 이것은 로버스트 국소다항회귀에 의해 추정된 비모수 회귀곡선이다. 극단값에 영향을 덜 받으면서 두 변수의 관계를 가장 잘 나타내는 곡선이라고 하겠다. 그림 5.4에서는 분산이 일정하지 않다는 증거를 확인하기 어려워 보인다.

\(\bullet\) 오차항의 정규분포 가정

회귀분석에서 이루어지는 검정 및 신뢰구간은 오차항이 정규분포를 한다는 가정에 근거를 두고 이루어진다. 그러나 오차항의 분포가 정규분포의 형태에서 약간 벗어나는 것은 큰 문제를 유발하지 않으며, 표본 크기가 커지면 중심극한정리를 적용할 수 있어서 비정규성은 큰 문제가 되지 않는다. 그러나 오차항의 분포가 Cauchy 분포와 같이 꼬리가 긴 형태의 분포임이 확인된다면 최소제곱법에 의한 회귀계수의 추정보다는 로버스트 선형회귀를 이용하는 것이 더 효과적일 것이다.

정규성의 확인에 사용되는 그래프로는 함수 plot()에서 생성되는 표준화잔차에 대한 정규 분위수-분위수 그래프가 있다. 회귀모형 fit_s의 정규성 가정을 확인해보자.

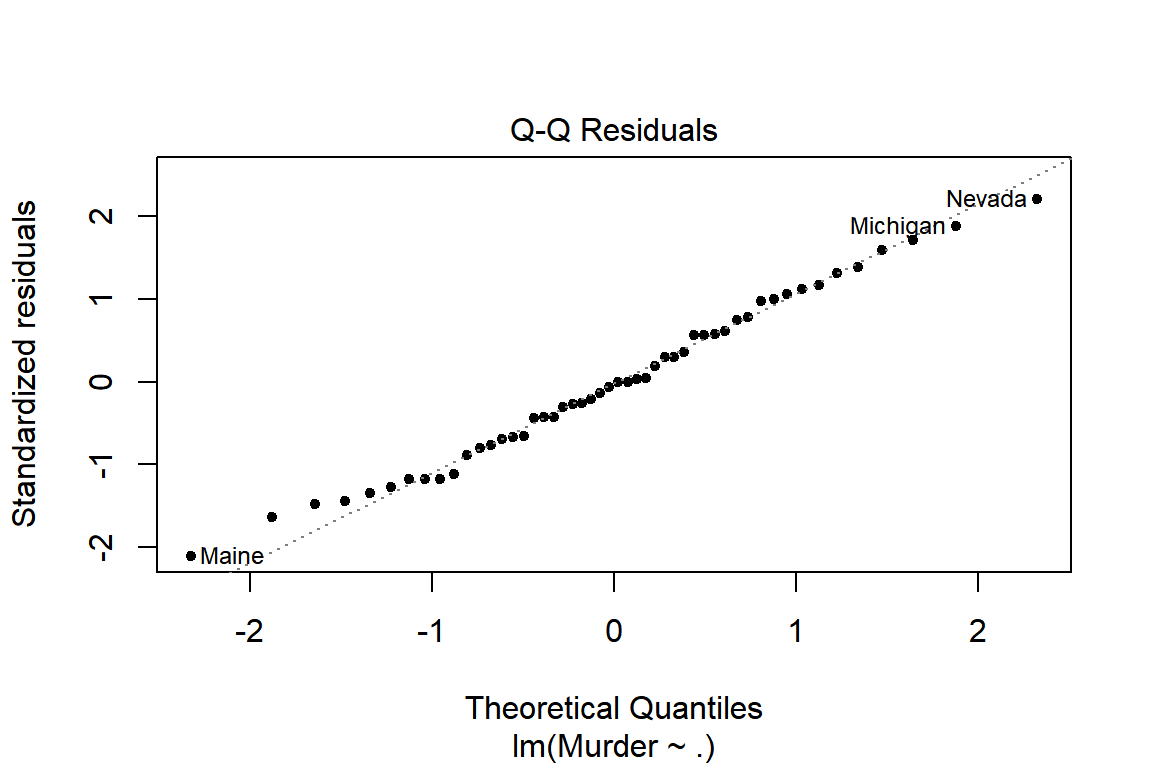
그림 5.5: 정규분포 가정 확인을 위한 그래프

잔차의 정규 분위수-분위수 그래프에서는 크기순으로 재배열한 잔차가 표본 분위수가 되는데, 표본 분위수 사이의 간격 패턴이 정규분포 이론 분위수 사이의 간격 패턴과 유사하면 점들이 기준선 위에 분포하게 된다. 정규분포 가정에는 문제가 없는 것으로 보인다.

\(\bullet\) 오차항의 독립성 가정

수집된 자료가 시간적 혹은 공간적으로 서로 연관되어 있는 경우에는 오차항의 독립성 가정이 만족되지 않을 수 있다. 시간에 흐름에 따라 관측된 시계열 자료나 공간에 따라 관측된 공간 자료를 대상으로 회귀분석을 하는 경우에는 반드시 확인해야 할 가정이 된다.

독립성 가정은 여러 행태로 위반될 수 있는데, 우선 \(\varepsilon_{i}\) 가 \(\varepsilon_{i-1}\) 와 서로 연관되어 있는지 여부, 즉 1차 자기상관관계만을 확인하려면 Durbin-Watson 검정을 실시하면 된다. Durbin-Watson 검정은 패키지 car의 함수 durbinWatsonTest()로 할 수 있으며, 귀무가설은 오차항의 1차 자기상관계수가 0이라는 것이다.

Durbin-Watson 검정에서 귀무가설을 기각하지 못했다고 해서 오차항이 독립이라고 바로 결론을 내릴 수는 없는데, 그것은 일반적인 형태의 위반 여부를 확인해야 하기 때문이다. 일반적인 형태의 독립성 위반이란 오차항이 자기회귀이동평균모형, 즉 ARMA(p,q)모형인지 여부를 확인하는 것이다. 이것을 위한 첫 번째 단계는 오차항의 1차 자기상관계수부터 K차 자기상관계수가 모두 0이라는 귀무가설을 검정하는 Breusch-Godfrey 검정을 실시하는 것이며, 이 작업은 패키지 forecast의 함수 checkresiduals()로 할 수 있다.

독립성 가정 검정은 이 책의 수준을 넘어서기 때문에, 자세한 내용은 생략하기로 한다.

데이터 프레임 states는 시간적 혹은 공간적으로 연관을 갖기 어려운 방식으로 수집되어 있기 때문에 오차항의 독립성 가정에는 큰 문제가 없는 경우라고 할 수 있다.

\(\bullet\) 선형관계 가정

단순회귀모형의 경우 반응변수와 설명변수의 선형관계는 두 변수의 산점도로 충분히 확인할 수 있다. 그러나 다중회귀모형의 경우에는 변수 \(X_{i}\) 와 \(Y\) 의 산점도 혹은 변수 \(X_{i}\) 와 잔차 \(e\) 산점도가 큰 의미를 갖지 못하게 되는데, 이것은 회귀모형에 포함된 다른 변수의 영향력을 확인할 수 없기 때문이다.

이러한 경우 부분잔차(partial residual)가 매우 유용하게 사용될 수 있다. 변수 \(X_{i}\) 의 부분잔차란 반응변수 \(Y\) 에서 모형에 포함된 다른 설명변수의 영향력이 제거된 잔차를 의미하는데, \(Y-\sum_{j \ne i}\hat{\beta}_{j}X_{j}\) 로 정의할 수 있다.

그런데 \(Y=\hat{Y} + e\) 가 되기 때문에, 부분잔차는 \(\hat{Y}+e-\sum_{j \ne i}\hat{\beta}_{j}X_{j}\) 로 표현되고, \(e + \hat{\beta}_{i}X_{i}\) 로 정리할 수 있다. 따라서 다중선형회귀모형에서 \(X_{i}\) 와 \(Y\) 의 선형관계는 변수 \(X_{i}\) 와 그 부분잔차 \(e + \hat{\beta}_{i}X_{i}\) 의 산점도로 확인할 수 있다.

데이터 프레임 states의 회귀모형 fit_s에 포함된 설명변수와 반응변수의 선형관계를 부분잔차 산점도를 작성하여 확인해 보자. 부분 잔차 산점도는 패키지 car의 crPlots()로 작성할 수 있는데, 이 그래프는 Component + Residual Plots라고도 불린다.

library(car)

crPlots(fit_s)

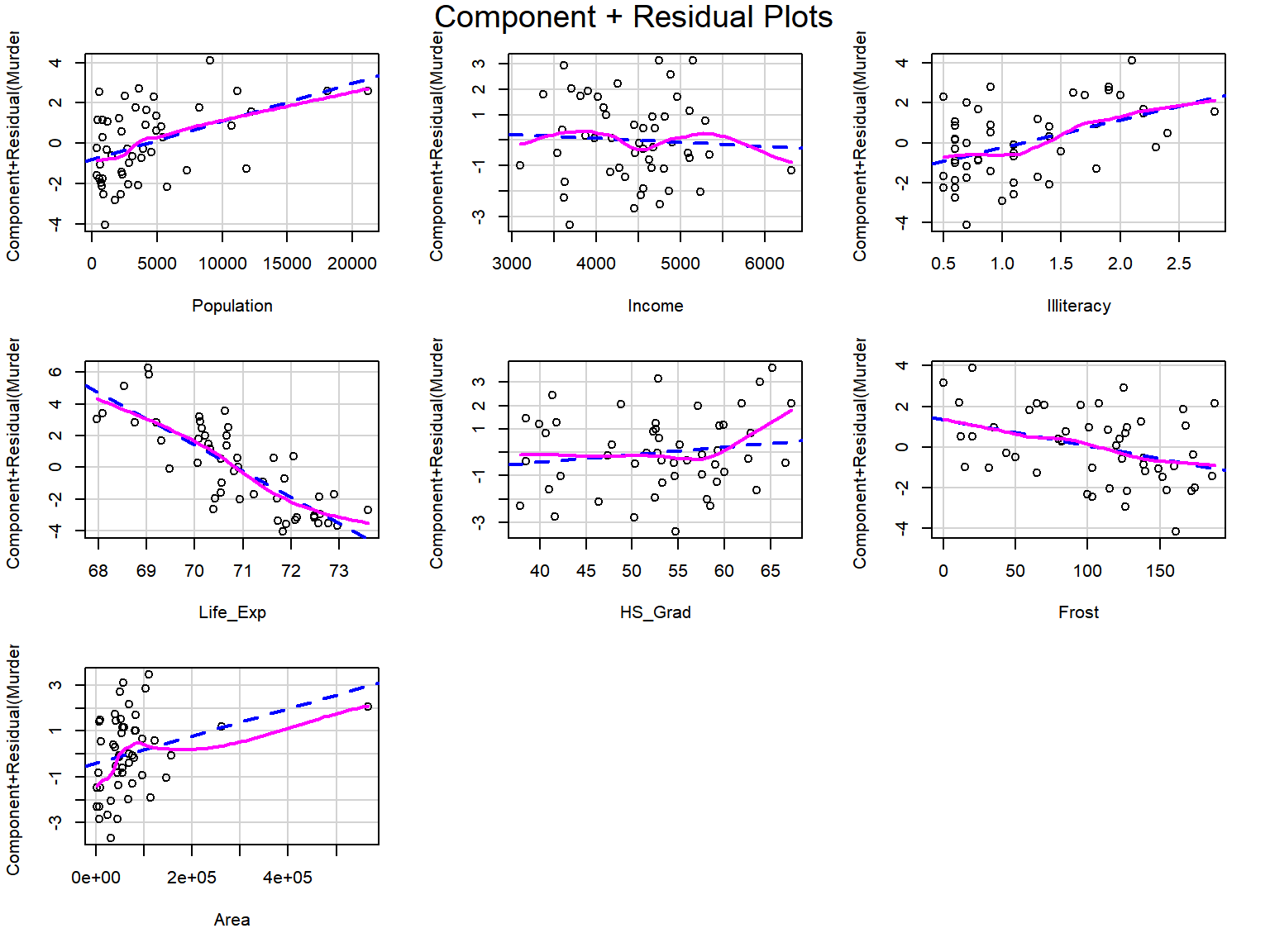
그림 5.6: 선형 가정 확인을 위한 부분잔차 산점도

각 변수의 부분잔차 산점도에는 두 변수의 회귀직선을 나타내는 파란 색의 대시(dashed line)와 국소다항회귀곡선을 나타내는 마젠타(magenta) 색의 실선이 추가되어 있다. 국소다항회귀곡선이 회귀직선과 큰 차이를 보인다면 비선형 관계를 의심할 수 있을 것이다. 그런 경우에는 해당 변수의 제곱항을 모형에 포함시키거나 또는 해당 변수의 적절한 변환이 이루어져야 할 것이다. 회귀모형 fit_s에서는 선형관계에 큰 문제가 없는 것으로 확인된다.

\(\bullet\) 다중공선성

다중공선성은 회귀모형의 가정과 직접적인 연관이 있는 것이 아니지만 회귀모형의 추정결과를 해석하는 과정에 큰 영향을 미칠 수 있는 문제가 된다. 즉, 설명변수들 사이에 강한 선형관계가 존재하는 다중공선성의 문제가 생기면 회귀계수 추정량의 분산이 크게 증가하게 되어 결과적으로 회귀계수의 신뢰구간 추정 및 검정에 큰 영향을 미치게 된다.

다중공선성은 분산팽창계수(VIF; Variance Inflation Factor)를 계산해 보면 확인할 수 있다. 변수 \(X_{j}\) 의 VIF는 \(1/(1-R_{j}^{2})\) 로 계산되는데, 여기에서 \(R_{j}^{2}\) 는 \(X_{j}\) 를 종속변수로 하고 나머지 설명변수를 독립변수로 하는 회귀모형의 결정계수이다.

변수 \(X_{j}\) 의 회귀계수 추정량인 \(\hat{\beta}_{j}\) 의 분산은 변수 \(X_{j}\) 의 VIF를 이용해서 다음과 같이 표현된다.

\[\begin{equation} Var(\hat{\beta}_{j}) = \frac{\sigma^{2}}{1-R_{j}^{2}} \end{equation}\]

수식에 의하면, VIF가 큰 값이 되면, \(\hat{\beta}_{j}\) 의 분산도 큰 값을 갖게 된다. 그런데 추정량의 분산이 커진다는 것은 추정 결과에 변동성이 커진다는 것을 의미하는 것이며, 따라서 추정 결과에 대한 신빙성이 많이 떨어지게 된다.

VIF 값에 대한 판단 기준을 일률적으로 제시하는 것은 적절하지 않은 것으로 보인다. 다만 VIF 값이 10 이상이 된다는 것은 \(R_{j}^{2}\) 의 값이 0.9 이상이라는 것이고, VIF 값이 5 이상이면, \(R_{j}^{2}\) 의 값이 0.8 이상이 되는 것인데, 특정 설명변수의 변동이 다른 설명변수로 80% 혹은 90% 이상 설명된다면, 해당 변수를 굳이 모형에 포함시킬 필요는 없는 것으로 보인다.

강한 다중공선성이 존재하는 경우에 특정 변수를 제거함으로써 문제를 해결할 수도 있지만, 대부분의 경우에는 다른 모형을 대안으로 사용해야 한다. Ridge 회귀모형과 같은 shrinkage 모형이 사용될 수 있으며, 관련이 있을 것 같은 설명변수들을 대상으로 주성분을 추출해서 설명변수로 대신 사용하는 방법도 대안으로 사용된다.

분산팽창계수의 계산은 패키지 car의 함수 vif()로 할 수 있다. 모형 fit_s의 다중공선성 존재 여부를 확인해 보자.

vif(fit_s)
## Population     Income Illiteracy   Life_Exp    HS_Grad      Frost       Area 
##   1.342691   1.989395   4.135956   1.901430   3.437276   2.373463   1.690625

회귀모형 fit_s에 있는 다섯 설명변수의 분산팽창계수가 모두 큰 값이 아닌 것으로 계산되었고, 따라서 다중공선성의 문제는 없는 것으로 보인다.

\(\bullet\) 예제 : mtcars

mtcars 자료에 대해 4.3.2절에서 이루어진 주된 분석은 다음과 같다.

mtcars_4 <- mtcars |> 
  select(!c(gear, carb)) |> 
  mutate(across(c(cyl, vs, am), as.factor))

mtcars_4 자료에 대하여 BIC를 기준으로 best subset selection에 의한 변수선택 결과로 wt, qsec, am이 선택되었다.

fit_bic <- lm(mpg ~ wt + qsec + am, mtcars_4)

모형 fit_bic에 대한 잔차분석을 진행해 보자. 잔차분석 결과에 큰 문제가 없다면, 회귀모형에 대한 가정을 대부분 만족하는 것으로 간주할 수 있고, 따라서 모형 fit_bic를 예측모형으로 사용할 수 있는 것이다. 하지만 중대한 문제가 발견이 된다면, 발견된 문제 해결을 위해 모형 수정을 진행해야 할 것이다.

이제 모형 fit_bic에 대한 기본 그래프를 작성하는 것으로 잔차분석을 진행해 보자.

par(mfrow = c(2, 2))
plot(fit_bic, pch = 20)
par(mfrow = c(1,1))

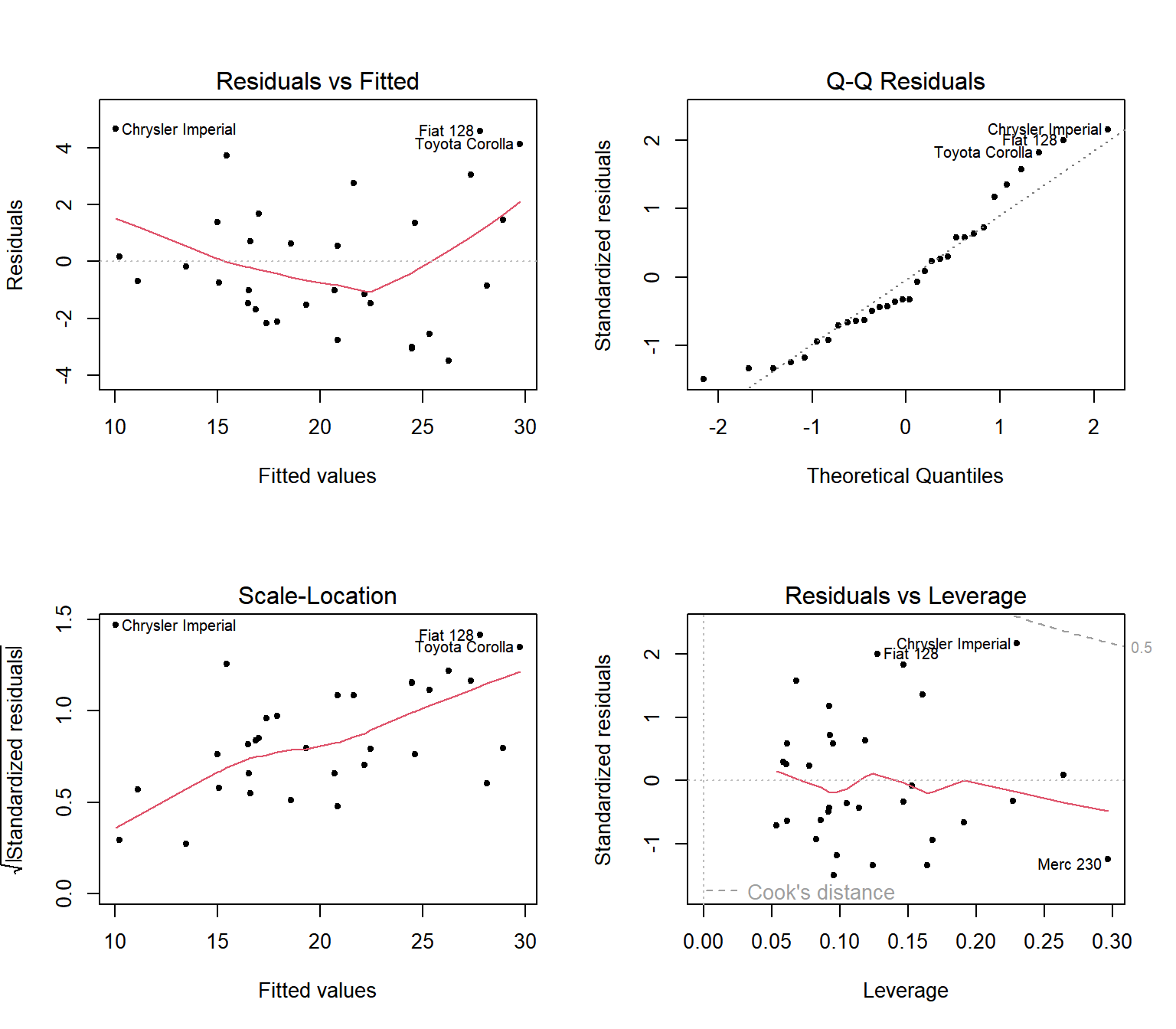
그림 5.7: mtcars 자료에 대한 모형 fit_bic의 잔차 산점도

Residuals vs Fitted라는 제목의 첫 번째 그래프에서 점들이 2차 함수 형태를 보이고 있음을 볼 수 있다. 이 현상은 일반적으로 반응변수와의 관계가 선형이 아닌 변수가 설명변수로 모형에 포함되면 발생하게 된다. 또한 Scale-Location이라는 제목의 세 번째 그래프에서 점들이 전체적으로 증가하는 패턴이 있음을 볼 수 있다. 이것은 일반적으로 오차항의 분산이 적합값이 증가하면 함께 증가할 때 발생하는 현상이다.

부분잔차 그래프를 작성해서 선형관계에 문제가 있는 변수를 확인해 보자.

crPlots(fit_bic, pch = 20)

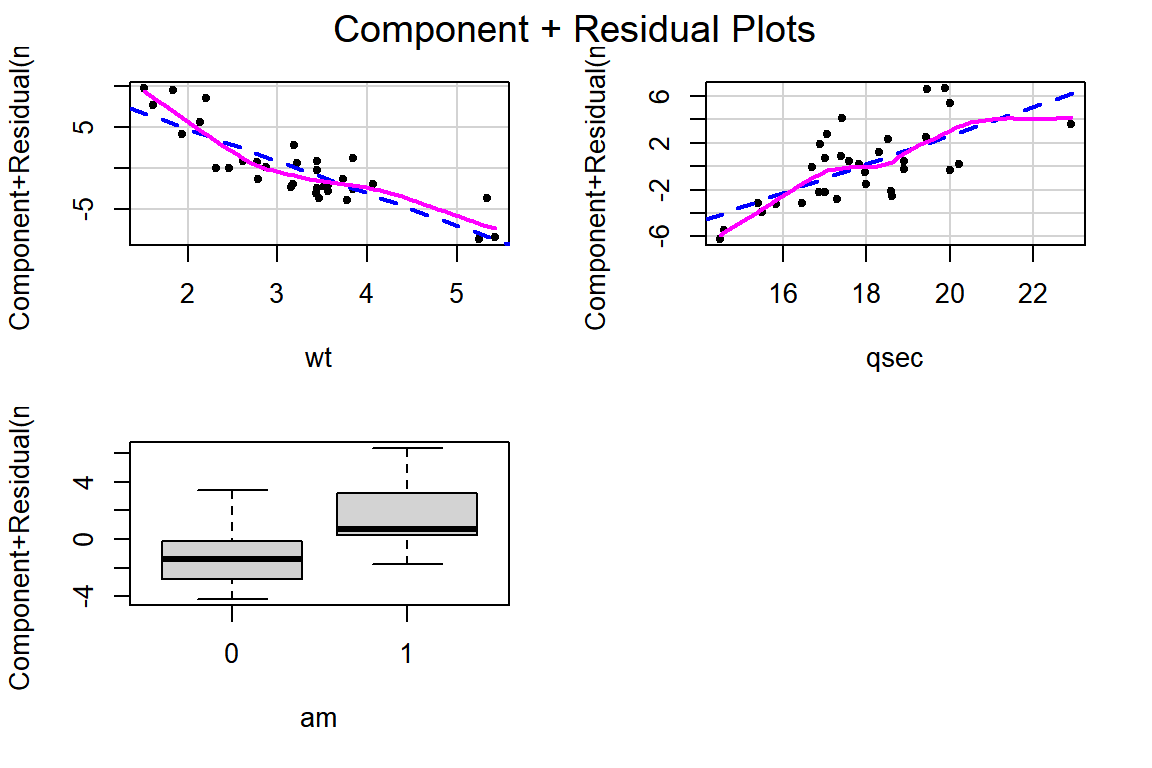
그림 5.8: mtcars 자료에 대한 모형 fit_bic의 부분잔차 그래프

변수 qsec의 경우에는 선형성에 큰 문제가 없는 것으로 보이지만, wt의 경우에는 선형으로 설명하기에 약간의 무리가 있는 것으로 보인다. 모형 fit_bic에 wt의 2차항을 포함시키고,적합 결과를 확인해보자.

fit_bic.1 <- update(fit_bic, . ~ . + I(wt^2))

summary(fit_bic.1)
## 
## Call:
## lm(formula = mpg ~ wt + qsec + am + I(wt^2), data = mtcars_4)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.7508 -1.3125 -0.4954  1.0722  4.8553 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  27.7376     8.9574   3.097 0.004528 ** 
## wt          -11.2491     2.6808  -4.196 0.000263 ***
## qsec          0.9705     0.2739   3.543 0.001461 ** 
## am1           1.0215     1.4346   0.712 0.482522    
## I(wt^2)       0.9582     0.3403   2.816 0.008978 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.201 on 27 degrees of freedom
## Multiple R-squared:  0.8838, Adjusted R-squared:  0.8666 
## F-statistic: 51.33 on 4 and 27 DF,  p-value: 3.107e-12

추가된 wt의 2차항이 유의하게 나왔고, 수정결정계수가 증가한 것으로 보아, wt의 2차항을 포함시키는 것이 좋을 것으로 보인다. 그러나 wt의 2차항이 포함됨으로써 am이 비유의적이 되었는데, 따라서 am을 제외한 모형을 적합시키고, 결과를 확인할 필요가 있다.

fit_bic.2 <- update(fit_bic.1, . ~ . - am)

summary(fit_bic.2)
## 
## Call:
## lm(formula = mpg ~ wt + qsec + I(wt^2), data = mtcars_4)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.2200 -1.2521 -0.6288  0.9357  5.1761 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  32.6418     5.6768   5.750 3.59e-06 ***
## wt          -12.4331     2.0842  -5.965 2.01e-06 ***
## qsec          0.8599     0.2236   3.846 0.000634 ***
## I(wt^2)       1.0730     0.2970   3.613 0.001174 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.182 on 28 degrees of freedom
## Multiple R-squared:  0.8816, Adjusted R-squared:  0.8689 
## F-statistic:  69.5 on 3 and 28 DF,  p-value: 4.345e-13

모형 fit_bic, fit_bic.1, fit_bic.2를 비교해 보자. AIC와 BIC, 그리고 수정결정계수를 비교해 보자.

AIC(fit_bic, fit_bic.1, fit_bic.2)
##           df      AIC
## fit_bic    5 154.1194
## fit_bic.1  6 147.8800
## fit_bic.2  5 146.4754

BIC(fit_bic, fit_bic.1, fit_bic.2)
##           df      BIC
## fit_bic    5 161.4481
## fit_bic.1  6 156.6744
## fit_bic.2  5 153.8040

summary(fit_bic)$adj.r.squared
## [1] 0.8335561

summary(fit_bic.1)$adj.r.squared
## [1] 0.8665743

summary(fit_bic.2)$adj.r.squared
## [1] 0.8689233

세 가지 기준에서 모형 fit_bic.2를 선택하는 것이 좋을 것으로 보인다. 이제 fit_bic.2에 대한 잔차분석을 다시 진행해 보자.

par(mfrow = c(2, 2))
plot(fit_bic.2, pch = 20)
par(mfrow = c(1, 1))

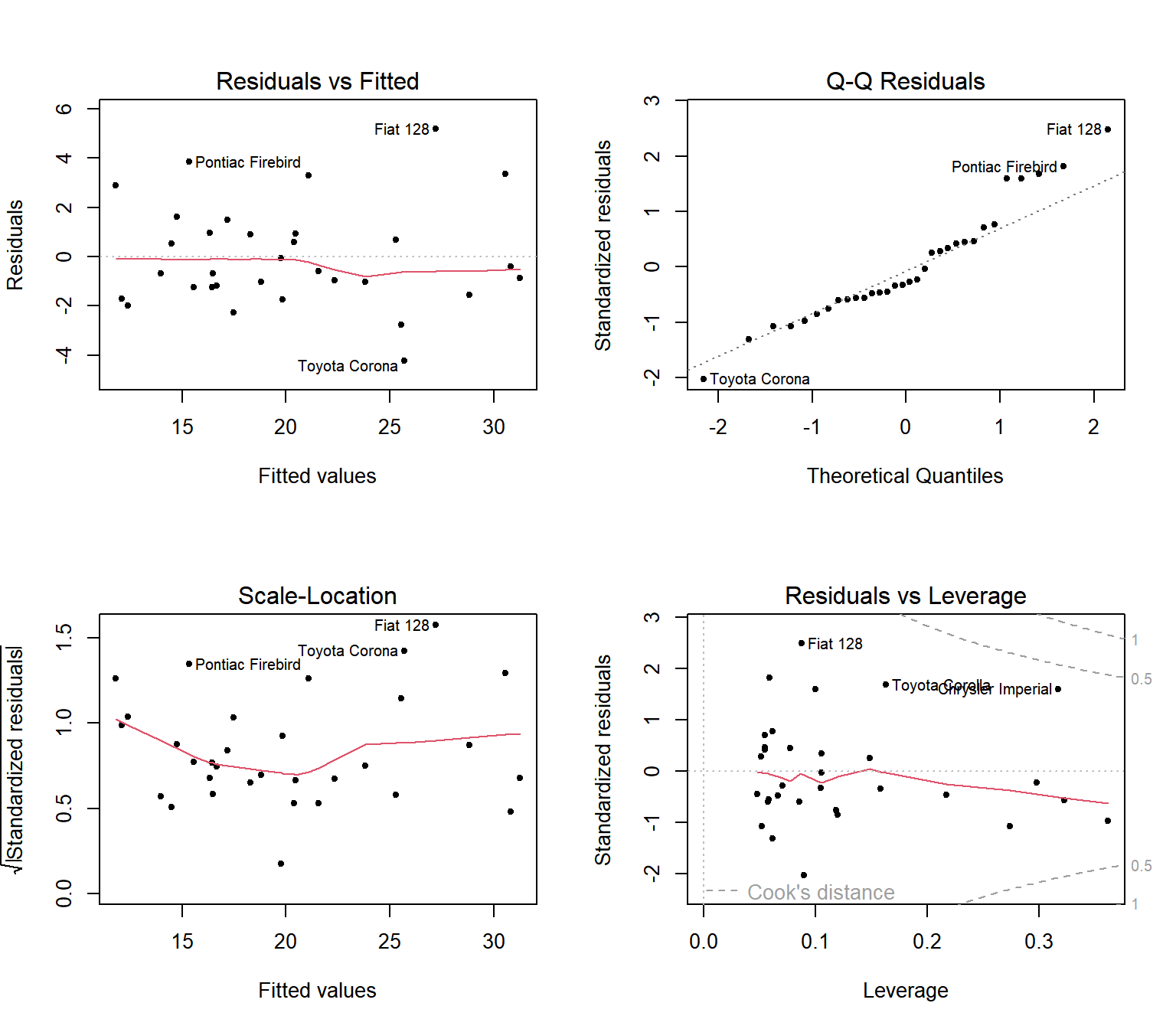
그림 5.9: 모형 fit_bic.2의 잔차분석 그래프

큰 문제는 없는 것으로 보인다. 부분잔차 그래프도 작성해 보자. 선형 가정이 만족되는 것으로 보인다.

crPlots(fit_bic.2, pch = 20)

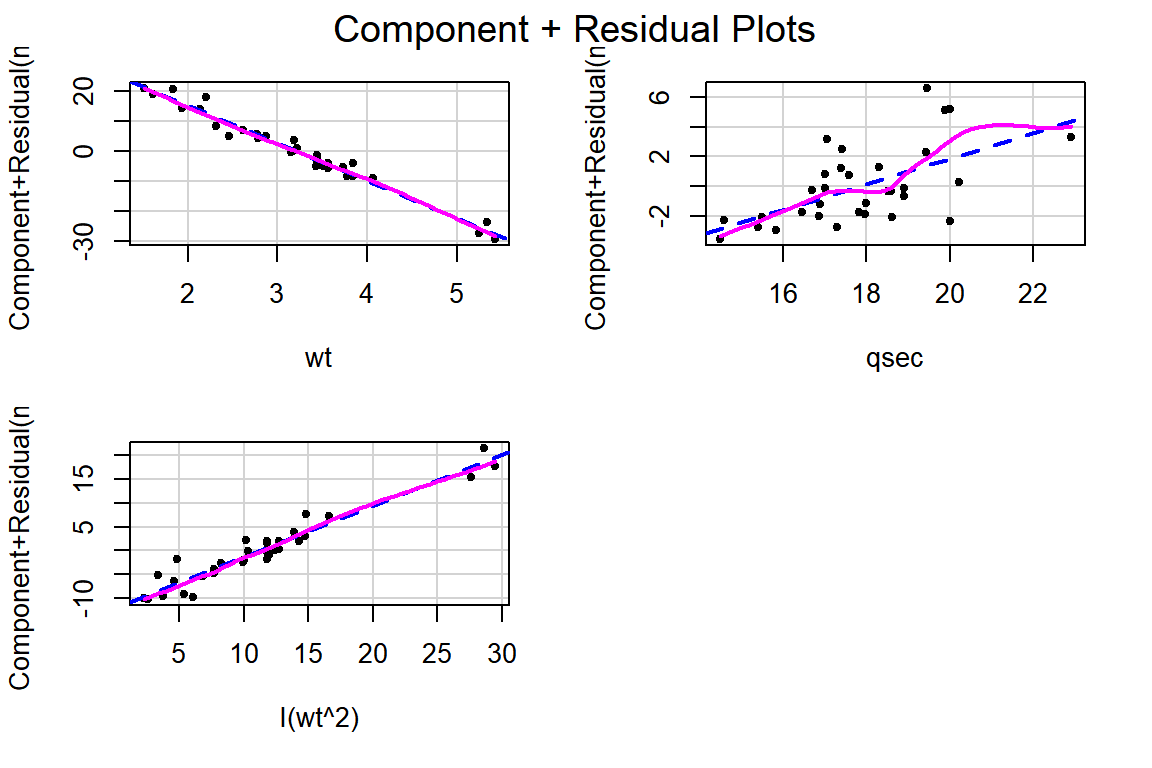
그림 5.10: 모형 fit_bic.2의 부분잔차 그래프

모형 fit_bic.2에 대한 다중공선성도 확인해 보자. 모형 fit_bic.2는 wt의 다항회귀모형이 되는데, 이런 경우에는 해당 변수 1차항과 2차항의 VIF 값은 상당히 큰 값으로 계산되는 것이 당연하다.

vif(fit_bic.2)
##        wt      qsec   I(wt^2) 
## 27.076669  1.039145 26.896784

이것은 다항회귀모형이 갖고 있는 구조적 문제인데, 따라서 가능한 낮은 차수를 유지하는 것이 필요한 것이다. 수정 전 모형인 fit_bic의 VIF를 확인해 보면, 다중공선성의 문제는 없는 것으로 보인다.

vif(fit_bic)
##       wt     qsec       am 
## 2.482952 1.364339 2.541437

5.2 관찰값에 대한 진단

회귀모형의 가정사항 만족 여부를 확인하는 것과 더불어 특이한 관찰값의 존재유무를 확인하는 것도 중요한 회귀진단 항목이 된다. 특이한 관찰값이란 회귀계수의 추정에 과도하게 큰 영향을 미치는 관찰값이나, 추정된 회귀모형으로는 설명이 잘 안 되는 이상값을 의미한다.

영향력이 큰 관찰값을 발견하는 데 필요한 통계량으로는 DFBETAS, DFFITS, Covariance ratio, Cook’s distance와 Leverage 등이 있다. DFBETAS는 \(i\) 번째 관찰값을 포함한 상태와 제외한 상태에서 각각 추정한 개별 회귀계수 추정값 \(\hat{\beta}_{j}\) 의 차이를 의미한다. DEFITS는 \(i\) 번째 관찰값을 포함한 상태와 제외한 상태에서 각각 추정한 적합값 \(\hat{y}_{i}\) 의 차이를 의미한다.

Cook’s distance는 \(i\) 번째 관찰값을 포함한 상태에서 추정한 회귀계수 벡터 \(\hat{\boldsymbol{\beta}}\) 과 \(i\) 번째 관찰값을 제외하고 추정한 회귀계수 벡터 \(\hat{\boldsymbol{\beta}}_{(i)}\) 의 통합된 차이를 보여주는 통계량이다.

\[\begin{equation} COOKD = \frac{\left(\hat{\boldsymbol{\beta}}-\hat{\boldsymbol{\beta}}_{(i)} \right)^{T}\mathbf{X}^{T}\mathbf{X}\left(\hat{\boldsymbol{\beta}}-\hat{\boldsymbol{\beta}}_{(i)} \right) }{(k+1)RSE} \end{equation}\]

스튜던트화 잔차 \(t_{i}\) 는 \(y_{i}\) 와 \(\hat{y}_{(i)}\) 의 표준화된 차이라고 할 수 있다.

\[\begin{equation} t_{i} = \frac{y_{i}-\hat{y}_{(i)}}{SE\left(y_{i}-\hat{y}_{(i)}\right)} \end{equation}\]

단, \(\hat{y}_{(i)}\) 를 \(i\) 번째 관찰값을 제외한 나머지 \((n-1)\) 개의 자료로 추정된 회귀모형으로 제외된 \(y_{i}\) 를 예측한 결과이다. 스튜던트화 잔차의 값이 크다는 것은 해당 관찰값이 이상값으로 분류될 가능성이 높다는 의미가 된다.

영향력이 큰 관찰값을 발견하는 데 필요한 통계량을 근거로 하여 특이한 관찰값 탐지에 사용되는 많은 R 함수가 있다. 그 중 패키지 car의 함수 influencePlot()에 대해 살펴보도록 하자. 이상값이란 추정된 회귀모형으로는 설명이 잘 안 되는 관찰값이라고 할 수 있는데, 대부분의 경우 이상값은 큰 잔차를 갖게 된다. 그러나 만일 이상값에 해당되는 관찰값이 영향력도 크다면 그림 5.3의 첫 번째 그래프에서 볼 수 있듯이 회귀계수의 추정을 왜곡시켜 그렇게 크지 않은 잔차를 갖게 될 수도 있다. 따라서 이상값을 판단하고자 한다면 일반적인 잔차보다는 스튜던트화 잔차를 이용하는 것이 더 효과적이라고 하겠다. 함수 influencePlot()은 스튜던트화 잔차와 레버리지, 그리고 Cook’s distance를 하나의 그래프에서 같이 보여줌으로써 특이한 관찰값을 분류하는 데 큰 도움이 되는 함수이다.

우선 5.1절에서 살펴본 states 자료에 대한 모형 fit_s를 대상으로 관찰값에 대한 진단을 실시해 보자.

library(car)

influencePlot(fit_s)

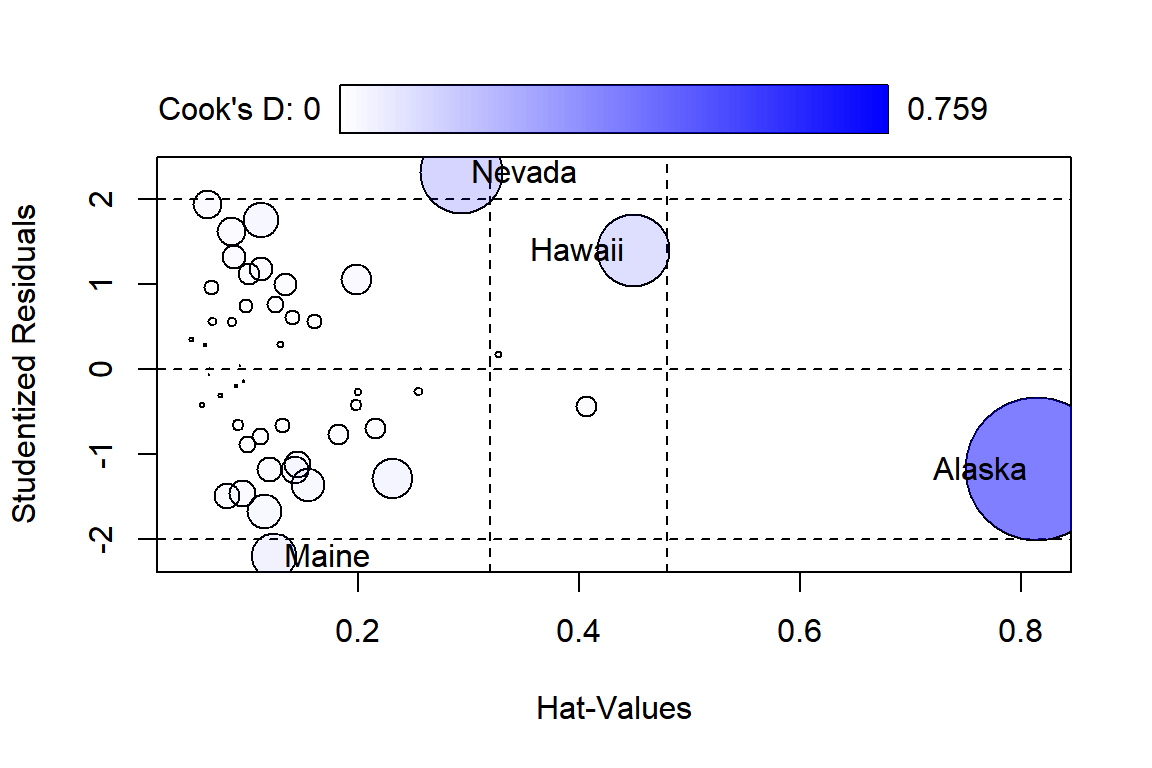
그림 5.11: 모형 fit_s에 대한 관찰값 진단

##          StudRes       Hat      CookD
## Alaska -1.180291 0.8147090 0.75856120
## Hawaii  1.402156 0.4494369 0.19610477
## Maine  -2.203220 0.1242744 0.07886962
## Nevada  2.316971 0.2937617 0.25282648

함수 influencePlot()으로 작성된 그래프는 각 관찰값의 레버리지를 X축 좌표로, 스튜던트화 잔차를 Y축 좌표로 하는 산점도이며, 점의 크기는 Cook’s distance에 비례하여 결정된다. 관찰값들의 평균 레버리지의 두 배와 세 배가 되는 지점에 수직 점선이 추가되며, 스튜던트화 잔차가 \(\pm 2\) 인 지점에 수평 점선이 추가된다. 또한 X축과 Y축에서 가장 극단적인 두 점에는 데이터 프레임의 행 이름이 라벨로 표시되며, 콘솔 창에 해당 관찰값의 레버리지(Hat), 스튜던트화 잔차(StudRes), Cook’s distance(CookD) 값이 출력된다.

그래프에서 확인할 수 있는 것으로는 우선 Alaska의 경우에 leverage 값과 Cook’s distance의 값이 제일 커서 영향력이 큰 관찰값이라 할 수 있지만, 스튜던트화 잔차는 비교적 크지 않다는 점이다. Nevada의 경우에는 Cook’s distance와 스튜던트화 잔차가 비교적 크지만, leverage는 작은 값을 갖고 있다. 전체적으로, 회귀모형 fit_s에는 문제가 되는 관찰값이 없다고 할 수 있다.

이번에는 5.1절에서 살펴본 mtcars 자료에 대한 모형 fit_bic.2를 대상으로 관찰값에 대한 진단을 실시해 보자.

influencePlot(fit_bic.2)

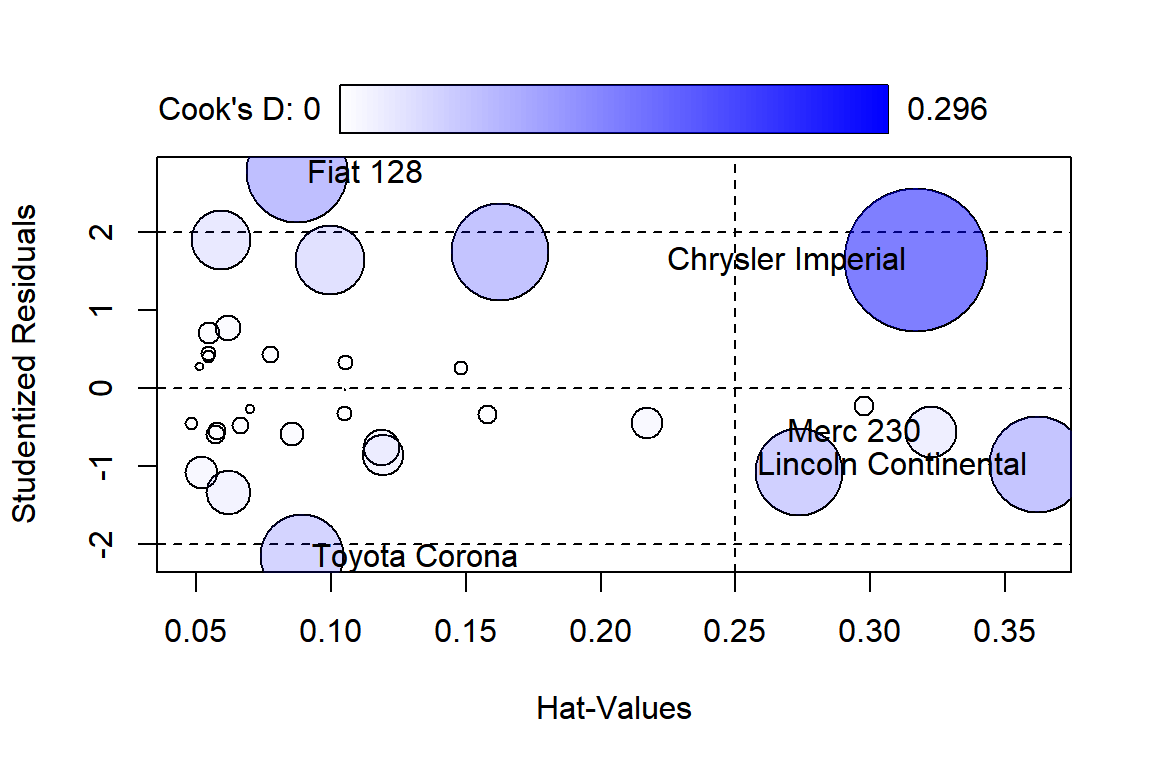
그림 5.12: 모형 fit_bic.2에 대한 관찰값 진단

##                        StudRes        Hat      CookD
## Merc 230            -0.5584214 0.32256309 0.03805547
## Lincoln Continental -0.9718419 0.36191253 0.13418893
## Chrysler Imperial    1.6442934 0.31694630 0.29564936
## Fiat 128             2.7615594 0.08752801 0.14788680
## Toyota Corona       -2.1542828 0.08927881 0.10065078

전체적으로, 회귀모형 fit_bic.2에도 큰 문제가 되는 관찰값은 없다고 할 수 있다.

5.3 연습문제

1. 반응변수 \(y\)에 대한 설명변수 \(x\)의 단순회귀모형 \(y_{i}=\beta_{0}+\beta_{1}x_{i}+\varepsilon_{i}, ~i=1,\ldots,n\) 을 적합하고자 한다.

각 개별 관찰값들이 X축 공간에서 자료의 중심에서 떨어져 있는 정도를 측정하는 통계량을 무엇이라 하는가?
’X축 공간에서 다른 자료와 멀리 떨어져 있는 자료는 모형의 적합에 큰 영향을 미칠 수 있으나, 그 자료가 실제 모형 적합에 미치는 영향이 크지 않을 수 있다.’라는 사실이 의미하는 바를 산점도 등을 이용하여 설명하라.
\(y_{i}\) 가 이상값이면 잔차 \(e_{i}\) 는 대부분 큰 값이 되겠지만, 어떤 경우에는 크지 않은 값을 갖게 되는데, 그 이유는 무엇인가? 또한 이러한 경우에 어떠한 척도를 사용하는 것이 더 유용한 정보를 얻을 수 있는가?

2. 다음 모형 적합 결과에 있는 문제점을 발견하라. 어떤 이유로 이러한 문제가 발생한 것으로 보이는가?

fit <- lm(y ~ x1 + x2, df1)
summary(fit)
## 
## Call:
## lm(formula = y ~ x1 + x2, data = df1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.6719 -0.5497 -0.0280  0.2701  3.7489 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   1.7532     0.3373   5.197 4.31e-06 ***
## x1           14.2673    16.1362   0.884    0.381    
## x2            2.8347     1.7842   1.589    0.119    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.162 on 47 degrees of freedom
## Multiple R-squared:  0.9907, Adjusted R-squared:  0.9903 
## F-statistic:  2500 on 2 and 47 DF,  p-value: < 2.2e-16

3. 데이터 프레임 auto_df에는 302대 차량의 연비와 관련된 자료가 입력되어 있다.

auto_df |> print(n = 3)
## # A tibble: 302 × 7
##     mpg cylinders displacement horsepower weight acceleration  year
##   <dbl> <fct>            <dbl>      <dbl>  <dbl>        <dbl> <dbl>
## 1    18 8                  307        130   3504         12      70
## 2    15 8                  350        165   3693         11.5    70
## 3    18 8                  318        150   3436         11      70
## # ℹ 299 more rows

회귀모형 auto_fit에 대한 회귀진단을 실시해 보자. 작성된 그래프를 근거로 확인할 수 있는 회귀모형의 가정 사항은 어떤 것이 있는가? 가정 사항은 만족하는 것으로 보이는가?

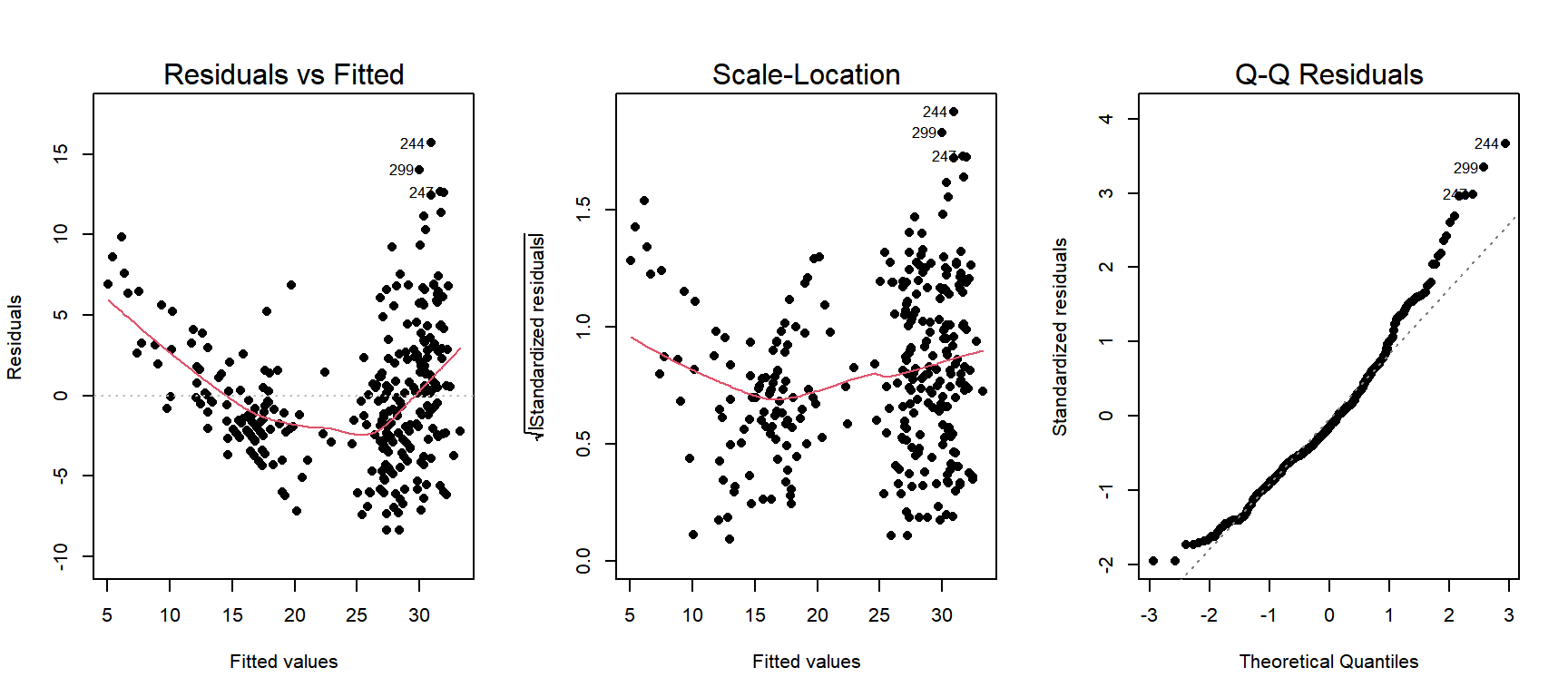
auto_fit <- lm(mpg ~ displacement + horsepower + acceleration, auto_df)

회귀모형 auto_fit의 적합에 사용된 관찰값에 대한 진단을 실시해 보자. 작성된 그래프에 사용된 통계량에 대해 설명하라. 문제가 되는 관찰값이 있는 것으로 보이는가?

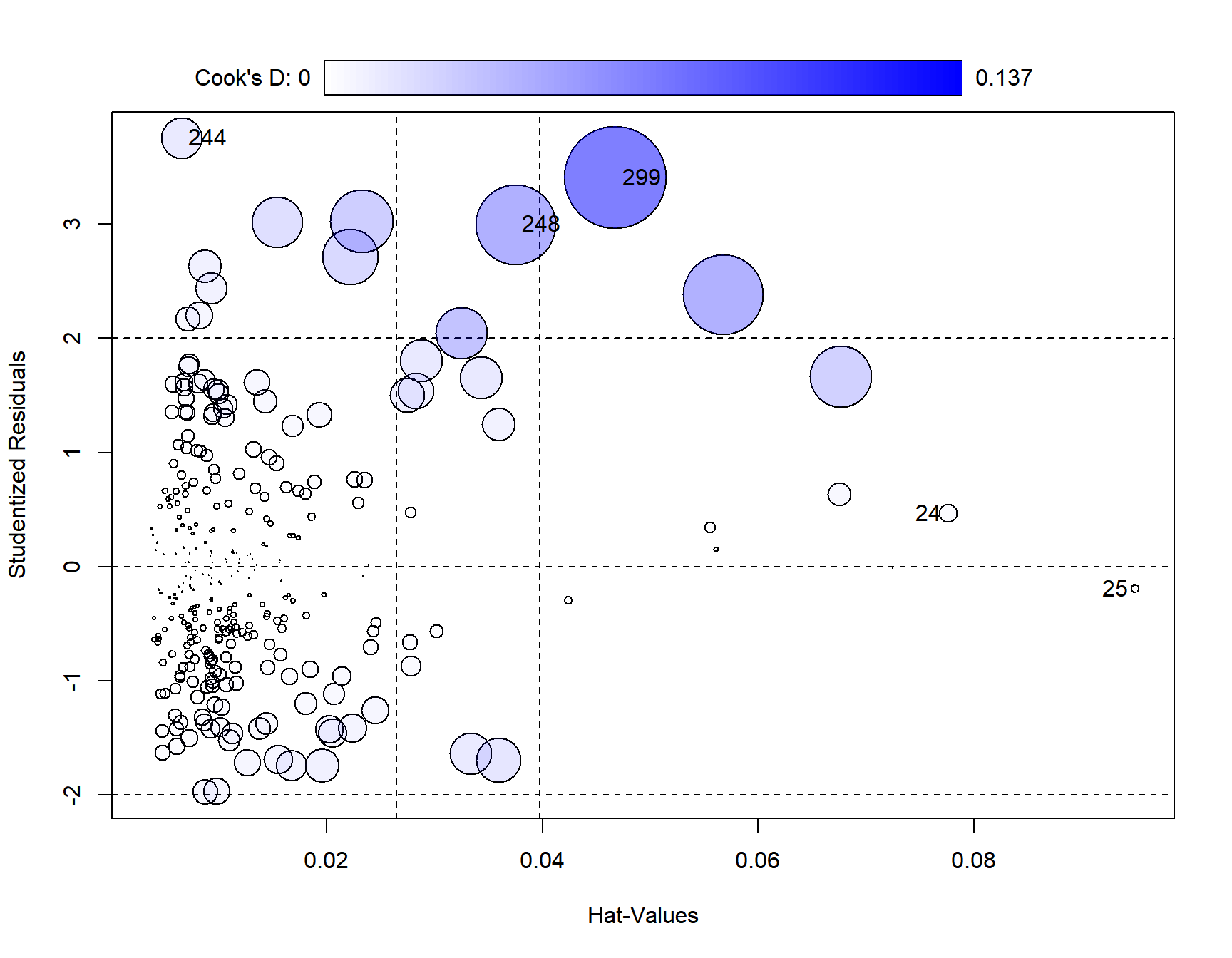
##        StudRes         Hat       CookD
## 24   0.4670488 0.077621531 0.004601278
## 25  -0.1939362 0.094916421 0.000989271
## 244  3.7497889 0.006560897 0.022240596
## 248  2.9957114 0.037488038 0.085105547
## 299  3.4040189 0.046791930 0.137323650