9 장 자료 탐색

수많은 변수들로 이루어져 있는 통계 자료가 주어지면 개별 변수들이 갖고 있는 정보를 탐색하는 것이 통계분석의 첫 단계가 된다. 개별 변수들의 정보를 따로따로 탐색하는 것은 결국 하나의 변수로 이루어진 일변량 자료를 탐색하는 것이라 할 수 있으며, 일변량 자료가 갖고 있는 정보 중 우리가 가장 관심을 두는 사항은 자료의 분포 형태가 될 것이다. 자료의 분포 형태를 그래프로 잘 표현하려면, 자료의 속성에 가장 적합한 그래프를 선택해야 한다.

한 변수를 대상으로 하는 일변량 자료의 탐색 과정이 끝나면, 두 변수를 동시에 고려하는 이변량 자료의 탐색을 시작해야 한다. 일변량 자료에 대해서는 자료의 분포에 대한 정보만이 필요했지만, 이변량 자료에 대해서는 각 자료의 분포에 대한 정보뿐 아니라, 두 변수의 분포를 비교하는 것과 두 변수 간의 관계가 중요한 정보가 된다.

이 장에서는 범주형 자료와 연속형 자료로 구분하여 각각의 경우에 자료 탐색에 사용할 수 있는 그래프의 작성방법을 살펴볼 것이다.

9.1 일변량 범주형 자료 탐색

여러 범주들로만 이루어진 범주형 자료는 명목형 자료와 순서형 자료로 구분된다. 명목형 자료란 범주들 간에 순서척도가 없는 경우로, 거주지, 성별, 종교 등이 여기에 해당되고, 순서형 자료란 강의 만족도와 같이 범주들을 순서에 따라 나열할 수 있는 경우를 지칭한다.

이 절에서는 막대그래프(bar chart), 파이그래프(pie chart)와 Cleveland의 점그래프(dot chart)를 사용하여 일변량 범주형 자료의 탐색 과정을 살펴볼 것인데, 이 그래프들은 명목형과 순서형 구분 없이 모두에게 잘 적용되는 그래프들이다.

9.1.1 막대그래프

범주형 자료에 대한 그래프로 가장 흔하게 볼 수 있는 그래프로서, 각 범주의 도수를 막대의 높이로 나타내는 그래프이다.

예제로 요인 state.region의 막대그래프를 작성해 보자. 요인 state.region는 미국 50개 주를 4개의 지역 범주로 구분한 명목형 자료이다.

state.region[1:10]
##  [1] South     West      West      South     West      West      Northeast
##  [8] South     South     South    
## Levels: Northeast South North Central West

함수 geom_bar()를 사용해서 막대그래프를 작성해 보자.

library(tidyverse)
tibble(state.region) |> 
  ggplot() +
  geom_bar(aes(x = state.region)) +
  xlab("Region")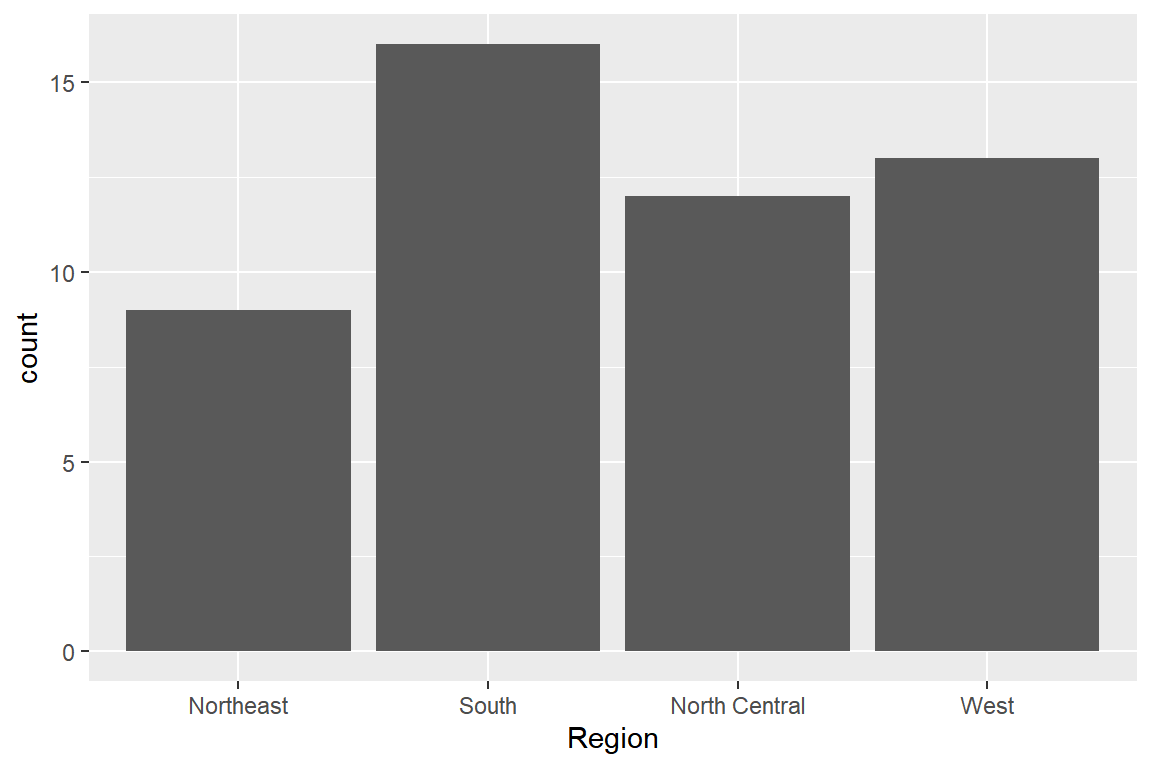
요인 `state.region`의 막대그래프

그림 9.1: 요인 state.region의 막대그래프

옆으로 누운 형태의 막대그래프도 작성해 보자.

tibble(state.region) |> 
  ggplot() +
  geom_bar(aes(y = state.region)) +
  ylab("Region")
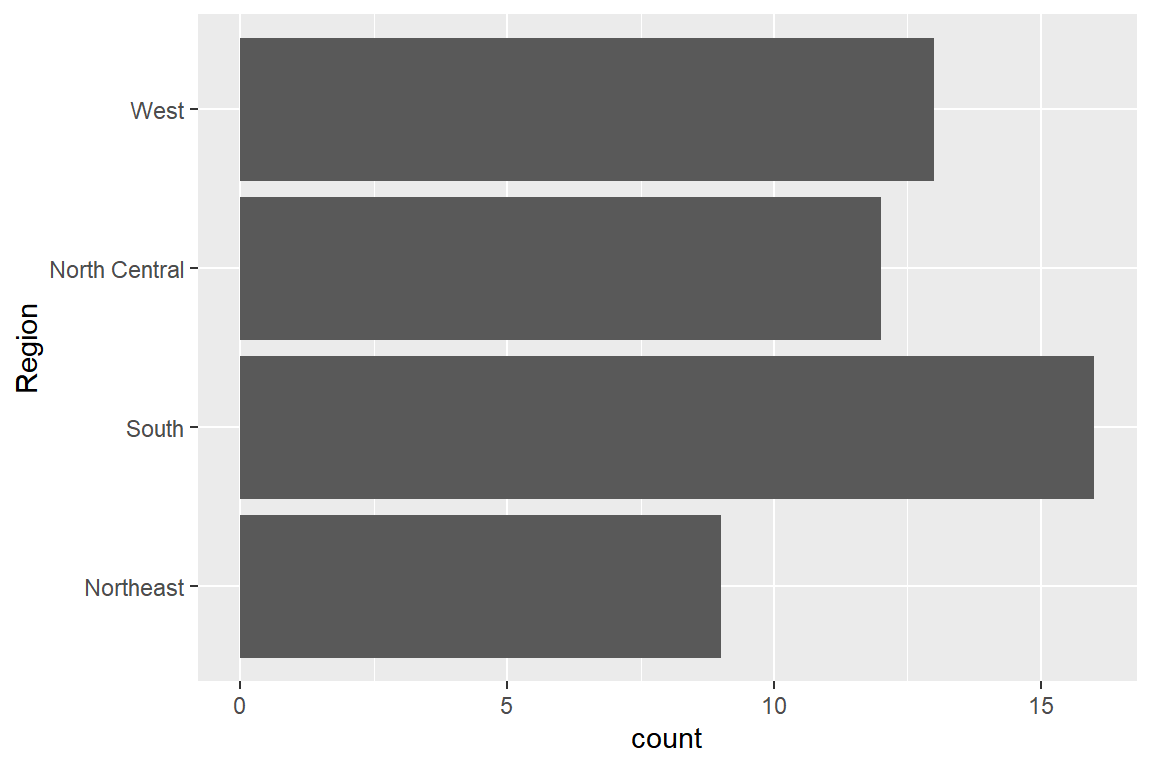
요인 `state.region`의 옆으로 누운 형태의 막대그래프

그림 9.2: 요인 state.region의 옆으로 누운 형태의 막대그래프

도수분포표가 자료로 주어진 경우에 막대그래프의 작성 방법을 살펴보자. 요인이 아닌 도수분포표를 자료로 사용하는 경우에는 함수 geom_bar()에 stat=“identity”를 추가하거나 geom_col()을 사용해야 한다.

요인 state.region을 데이터 프레임으로 전환하고, 함수 count()로 계산한 각 범주에 대한 도수가 변수로 포함된 데이터 프레임 df_1을 생성하자.

df_1 <- tibble(state.region) |> 
  count(state.region)
df_1
## # A tibble: 4 × 2
##   state.region      n
##   <fct>         <int>
## 1 Northeast         9
## 2 South            16
## 3 North Central    12
## 4 West             13

함수 geom_col()에서 데이터 프레임 df_1의 변수 중 범주를 나타내는 state.region과 각 범주의 도수를 나타내는 n을 시각적 요소 x, y에 매핑하면 막대그래프를 작성할 수 있다.

library(patchwork)
bar1 <- ggplot(df_1, aes(x = state.region, y = n)) +
  geom_col(fill = "steelblue") +
  labs(x = NULL, y = NULL)
bar2 <- bar1 + coord_flip()
bar1 + bar2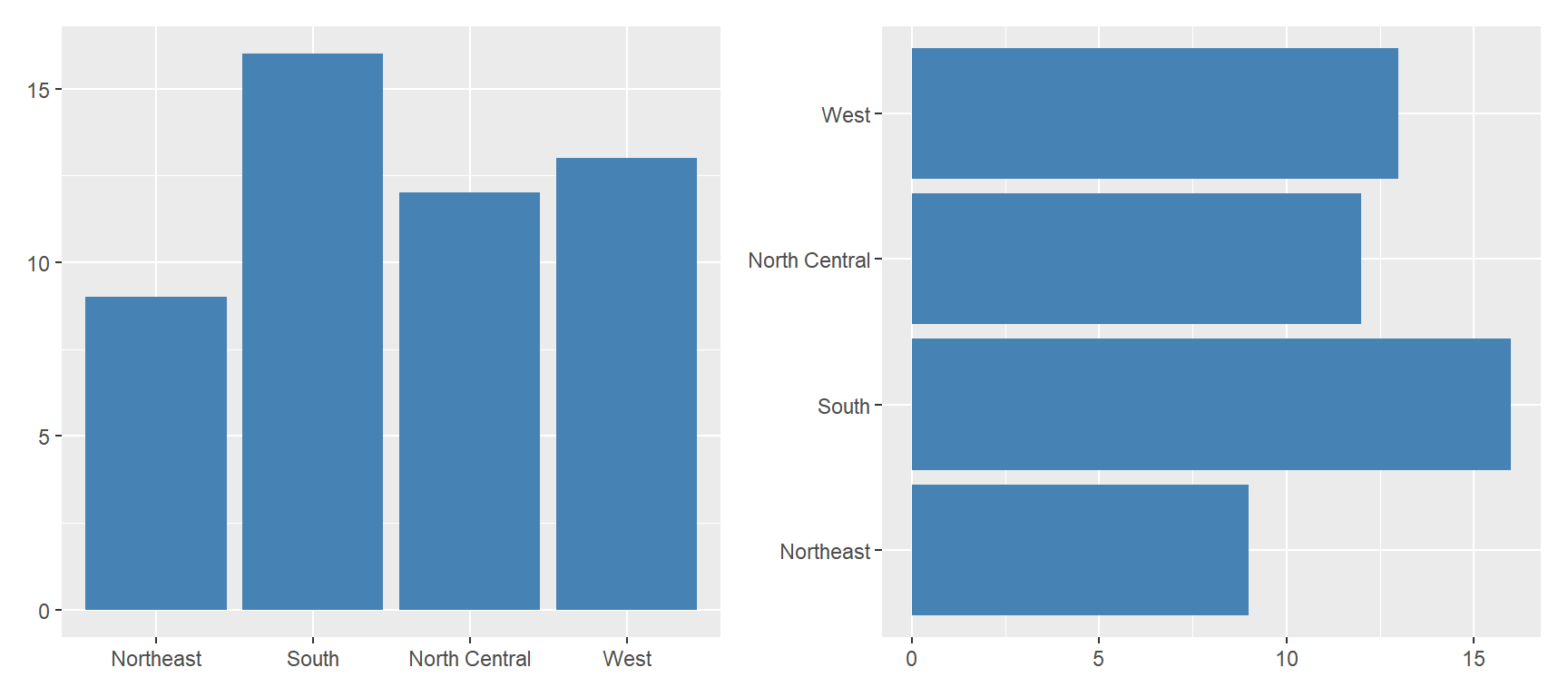
도수분포표가 자료로 주어진 경우의 막대그래프 작성

그림 9.3: 도수분포표가 자료로 주어진 경우의 막대그래프 작성

많은 경우에 막대그래프는 각 범주의 빈도를 이용하여 작성되지만, 경우에 따라서는 각 범주의 상대도수를 이용하여 작성해야 할 때도 있다. 이런 경우에는 함수 geom_bar()에서 생성된 변수 after_stat(prop)를 매핑하면서, 시각적 요소 group에 하나의 값을 지정해 주면 된다.

tibble(state.region) |> 
  ggplot() +
  geom_bar(aes(x = state.region, y = after_stat(prop), group = 1),
           fill = "skyblue") +
  labs(x = "Region", y = "Proportion")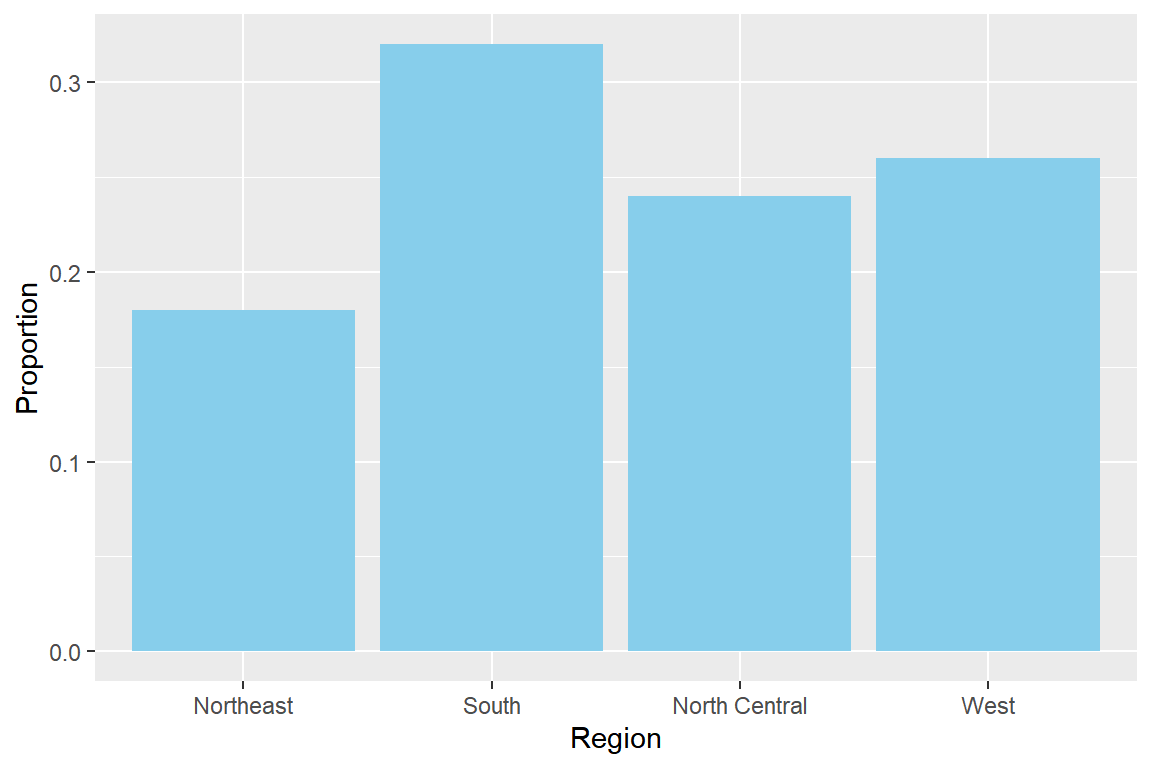
상대도수에 의한 막대그래프

그림 9.4: 상대도수에 의한 막대그래프

9.1.2 파이그래프

범주형 자료에 대한 그래프로 실생활에서 많이 사용되는 그래프 중 하나가 바로 파이그래프일 것이다. 파이그래프는 각 범주의 상대도수에 비례한 면적으로 원을 나누어 나타내는 그래프이다. 그러나 면적의 차이를 시각적으로 구분하는 것은 길이의 차이를 구분하는 것보다 훨씬 어렵기 때문에 대부분의 통계학자들은 파이그래프의 가치를 막대그래프보다 낮게 평가하고 있다. 파이조각의 면적을 비교하는 데 도움을 줄 수 있는 방안으로 각 파이 조각에 면적의 백분율을 라벨로 추가해 주는 것을 생각해 볼 수 있다.

파이그래프를 작성하기 위해서는 함수 geom_bar()에 시각적 요소 fill을 사용하여 쌓아올린 막대그래프를 작성하고, 함수 coord_polar()에서 theta에 “y”를 연결하여 상대도수에 비례한 각도를 계산해야 한다.

tibble(state.region) |> 
  ggplot() +
  geom_bar(aes(x = "", fill = state.region), width = 1) +
  labs(x = NULL, y = NULL) +
  coord_polar(theta = "y")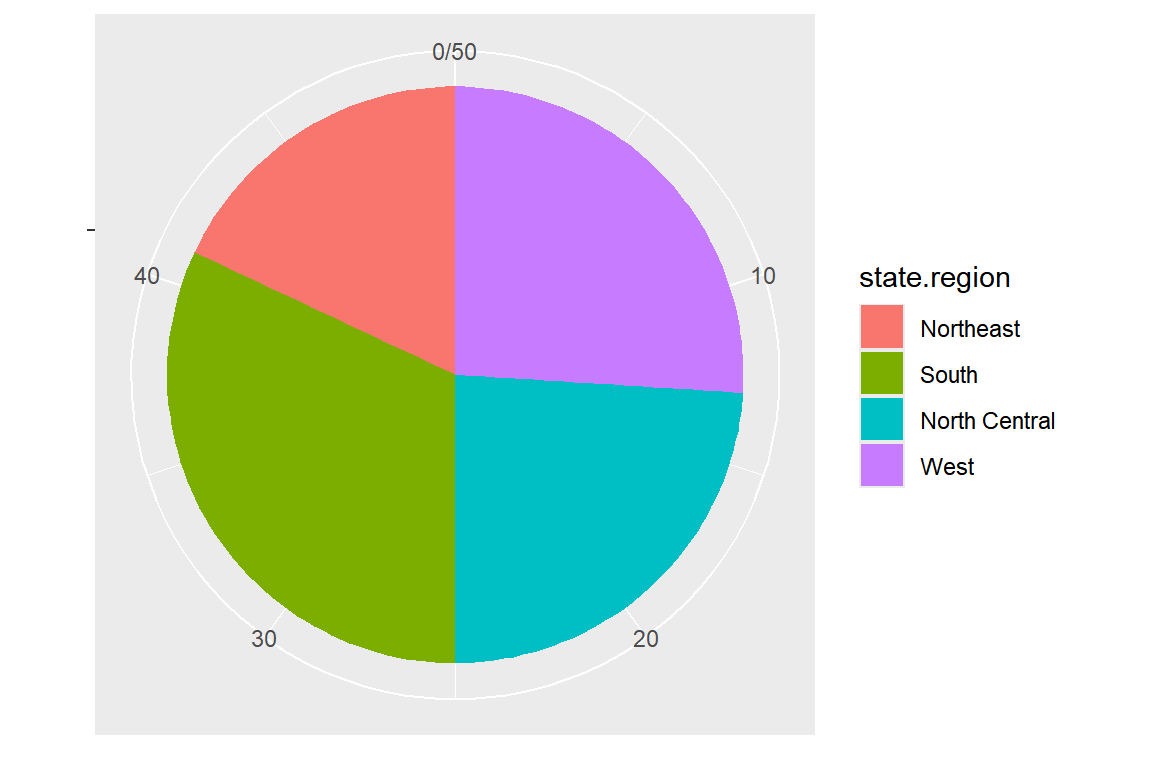
요인 `state.region`의 파이그래프

그림 9.5: 요인 state.region의 파이그래프

각 파이 조각의 비교를 돕기 위한 하나의 방안으로 백분율을 각 조각의 라벨로 추가해 보자. 이 경우에 라벨로 사용할 각 조각의 백분율을 데이터 프레임에 변수로 포함시키는 것이 필요하다. 숫자를 ‘%’ 기호가 포함된 백분율로 변환할 때 편하게 사용할 수 있는 함수가 패키지 scales에 있는 percent()이다.

요인 state.region을 데이터 프레임으로 전환하고, 각 범주에 대한 도수 및 백분율을 추가해서 df_2를 만들어 보자.

library(scales)
df_2 <- 
  tibble(state.region) |> 
  count(state.region) |> 
  mutate(pct = percent(n/sum(n))) |> 
  print()
## # A tibble: 4 × 3
##   state.region      n pct  
##   <fct>         <int> <chr>
## 1 Northeast         9 18%  
## 2 South            16 32%  
## 3 North Central    12 24%  
## 4 West             13 26%

이제 파이그래프를 작성하기 바로 전 단계인 쌓아 올린 막대그래프를 작성해 보자. 그림 9.6에서 볼 수 있듯이 쌓아 올려지는 조각의 순서는 데이터 프레임 df_2의 첫 번째 행 이 제일 위에 위치하고 두 번째 행이 그 밑으로 배치되는 위에서 아래 방향이 된다.

그래프에 라벨 추가는 함수 geom_text()로 할 수 있다. 데이터 프레임 df_2의 변수 pct를 시각적 요소 label에 매핑하고, 라벨의 위치를 position에 지정하면 되는데, 쌓아 올려진 각 조각의 중간 부분이 적절할 것으로 보여서 함수 position_stack()에서 변수 vjust에 0.5를 지정했다.

df_2 |> 
  ggplot(aes(x = "", y = n, fill = state.region)) + 
  geom_col(width = 1) +
  geom_text(aes(label = pct), size = 5,
            position = position_stack(vjust = 0.5)) +
  labs(x = NULL, y = NULL, fill = NULL)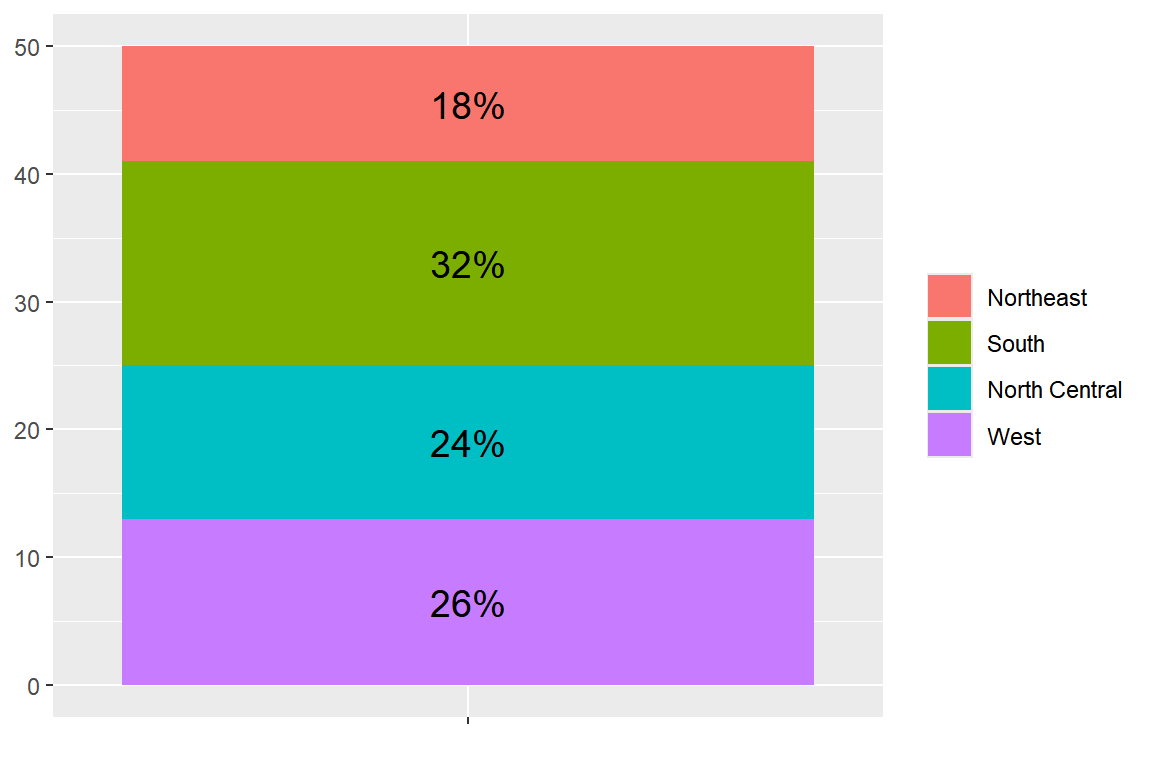
쌓아올린 막대그래프에 백분율 라벨 추가하기

그림 9.6: 쌓아올린 막대그래프에 백분율 라벨 추가하기

쌓아올린 막대그래프에 함수 coord_polar()를 적용시켜 파이그래프를 작성해 보자.

df_2 |> 
  ggplot(aes(x = "", y = n, fill = state.region)) + 
  geom_col(width = 1) +
  geom_text(aes(label = pct), size = 5,
            position = position_stack(vjust = 0.5)) +
  labs(x = NULL, y = NULL, fill = NULL) +
  coord_polar(theta = "y") +
  theme_void()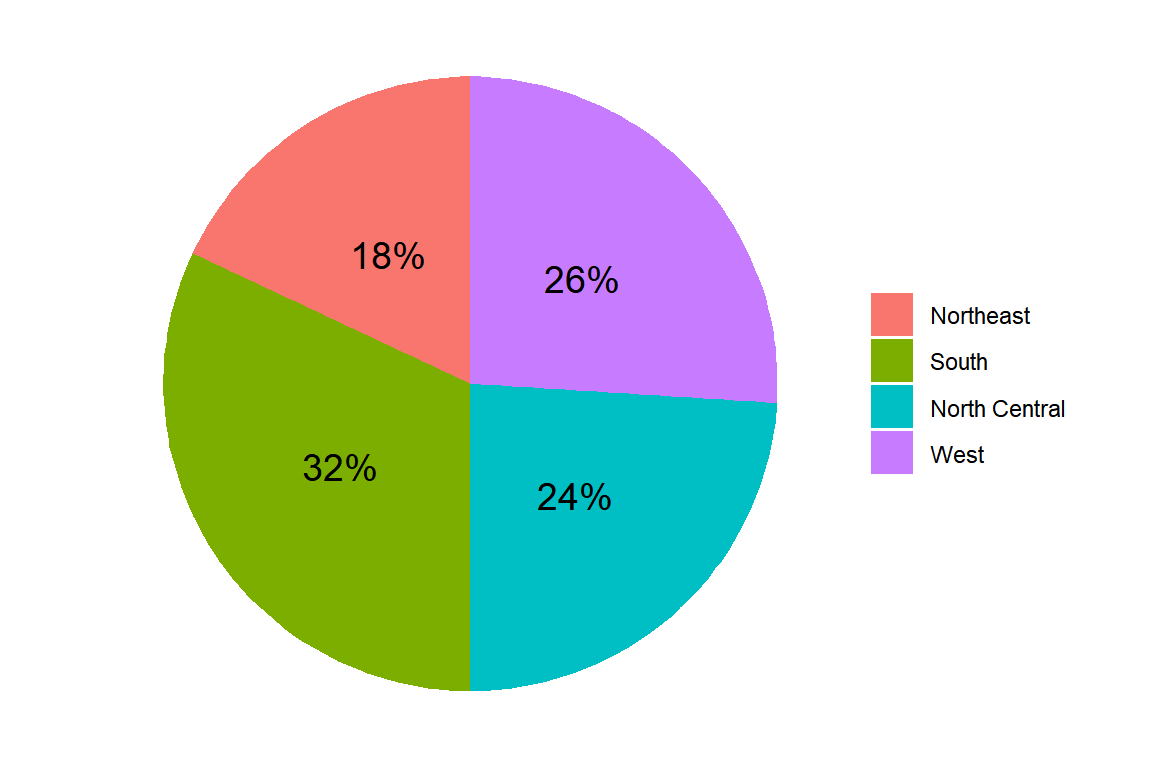
각 조각에 벡분율을 라벨로 추가한 파이그래프

그림 9.7: 각 조각에 벡분율을 라벨로 추가한 파이그래프

신문이나 잡지 등에 작성된 파이그래프 중에는 3차원 효과를 준 파이그래프도 종종 발견된다. 3D 파이그래프는 패키지 plotrix의 함수 pie3D()로 작성할 수 있다. 3차원 파이그래프도 파이그래프가 갖고 있는 근본적인 문제에서 자유로울 수는 없으며, 따라서 비록 시각적으로는 화려한 그래프이지만 정보의 효과적인 전달이라는 측면에서는 문제가 많은 그래프라고 할 수 있다.

library(plotrix)
pie_val <- df_2$n
pie_lab <- with(df_2, paste(state.region, pct))
pie3D(pie_val, explode = 0.1, labels = pie_lab)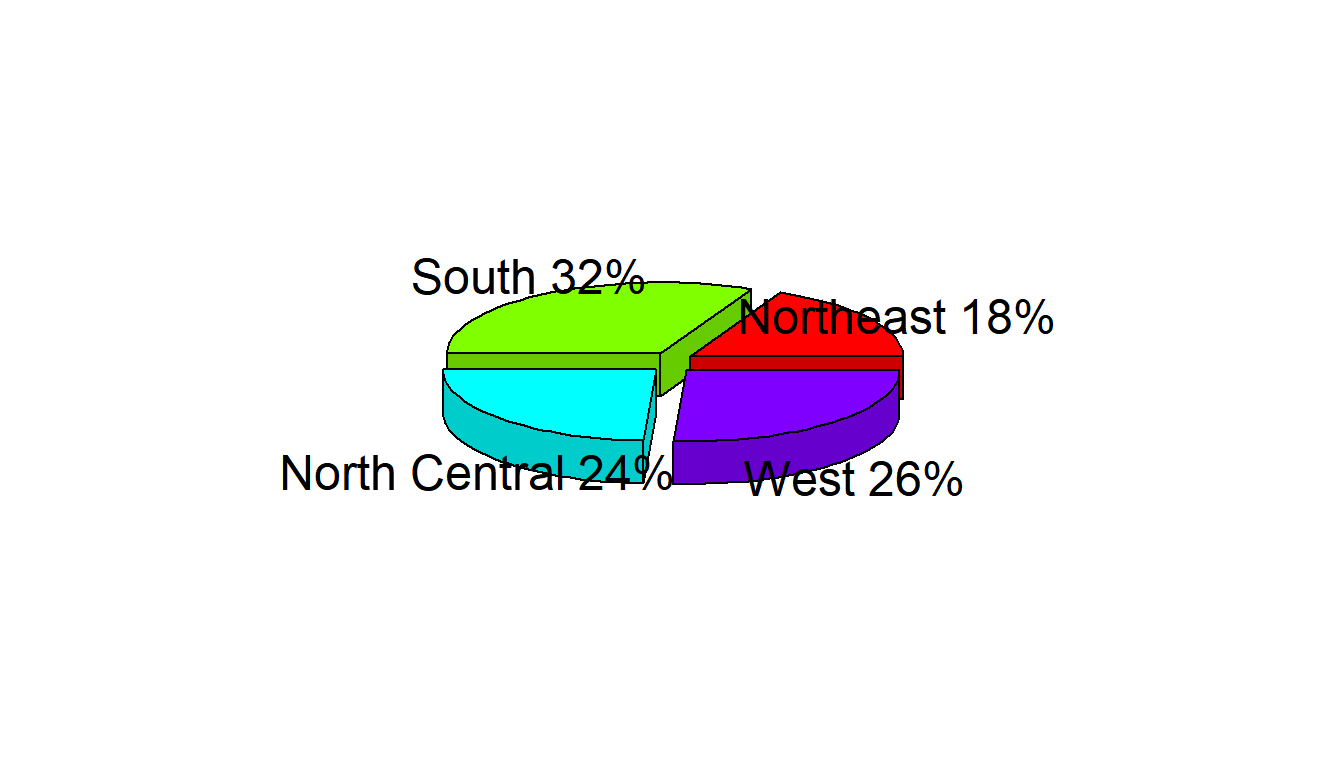
패키지 `plotrix`의 3차원 파이그래프

그림 9.8: 패키지 plotrix의 3차원 파이그래프

파이그래프의 가장 큰 문제는 파이조각들의 면적을 서로 비교하는 것이 매우 힘들다는 점이다. 이러한 문제를 해결하는 방안으로 제시된 그래프가 fan plot이다. R에서는 패키지 plotrix에 함수 fan.plot()으로 작성할 수 있다. Fan plot에서는 조각들이 크기순으로 서로 겹치도록 재배치되는데, 조각의 반지름을 조절하여 모든 조각을 볼 수 있도록 하였다. 그림 9.9에서 우리는 조각의 크기가 South > West > North Central > Northeast의 순서로 되어 있음을 쉽게 알 수 있다. 많이 사용되고 있지는 않지만 파이그래프보다는 훨씬 효과적인 그래프라고 할 수 있다.

fan.plot(pie_val, labels = pie_lab)
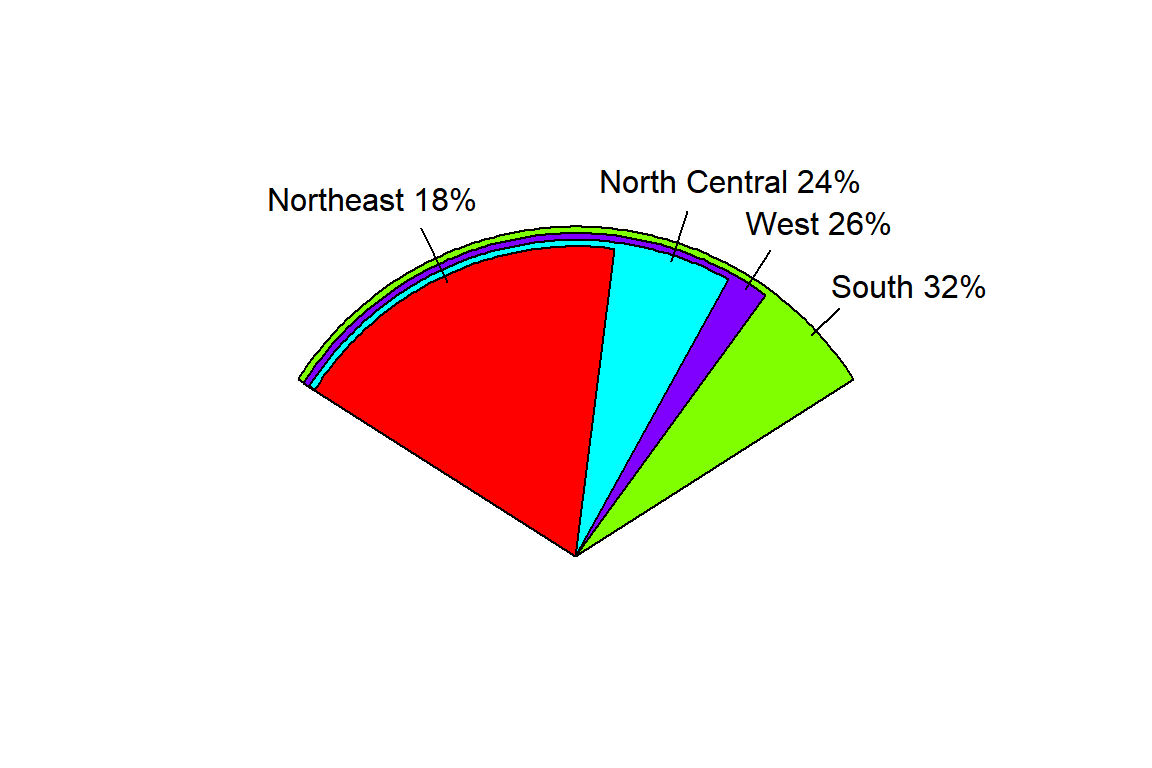
패키지 `plotrix`의 Fan plot

그림 9.9: 패키지 plotrix의 Fan plot

9.1.3 Cleveland의 점그래프

점 그래프는 통계 그래픽스 분야에 큰 기여를 한 Cleveland가 개발한 그래프이다. 비록 막대그래프나 파이그래프처럼 화려하게 치장할 수는 없으나 범주형 데이터의 속성을 정확 하게 표시할 수 있는 이상적인 그래프로 인정받고 있다.

예제 데이터로는 앞 절에서 살펴본 state.region을 다시 사용해 보자. 점그래프 작성은 도수분포표 자료인 df_1을 함수 geom_point()에 적용시키면 된다. 함수 theme()은 그래프의 디폴트 형태를 변경하고자 할 때 사용되는 것으로, 이 경우에는 그래프에 수평선을 추가하기 위해 사용되었다.

df_1 |> 
  ggplot(aes(x = n, y = state.region)) +
  geom_point(size = 2) +
  theme(panel.grid.major.y = element_line(linetype = 3, colour = "gray40")) +
  labs(x = NULL, y = NULL)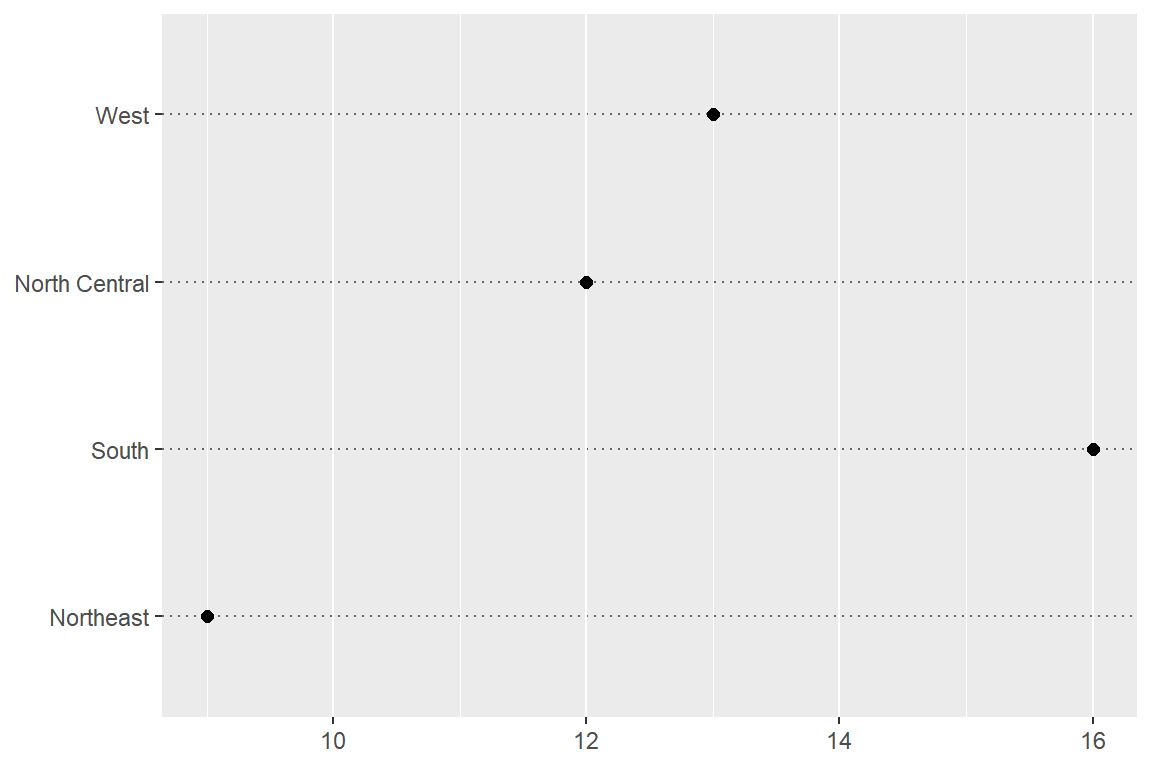
요인 `state.region`의 점그래프

그림 9.10: 요인 state.region의 점그래프

9.2 이변량 및 다변량 범주형 자료 탐색

범주형 자료가 주어지면 가장 먼저 해야 할 작업은 도수분포표 혹은 분할표를 작성하는 것이다. 이 절에서는 일변량 범주형 자료에 대한 도수분포표의 작성과 이변량 범주형 자료의 분할표의 작성에 사용할 수 있는 R 함수를 살펴볼 것이다. 또한 2차원 분할표로 정리된 자료를 효과적으로 시각화할 수 있는 그래프 작성법도 살펴볼 것이다.

9.2.1 분할표 작성

R에는 도수분포표 및 분할표를 작성하는 데 사용되는 몇 가지 함수가 있다. 그중 많이 사용되는 함수들이 다음의 표에 정리되어 있다.

도수분포표 및 분할표 작성에 관련된 함수
함수 대략의 기능
table(var1, var2, … , varN) N개의 범주형 변수로 N차원 분할표 작성
xtab(formula, data) data의 범주형 변수를 formula 에 정의된 방식으로 분할표 작성
prop.table(table, margins) 작성된 분할표의 결합분포 또는 margins 로 정의된 방향으로 조건분포 작성
margin.table(table, margins) 작성된 분할표의 한계분포를 margins 로 정의된 방향으로 작성
addmargins(table, margins) 작성된 분할표에 margins로 정의된 방향의 한계분포를 추가

위 함수들의 사용법을 예제를 이용하여 살펴보자. 예제로 사용할 자료는 패키지 vcd에 있는 데이터 프레임 Arthritis이다. 이 자료는 류머티즘 관절염 환자들을 대상으로 새로운 치료법의 효과를 알아보기 위해 이루어진 임상실험 자료이다.

data(Arthritis, package = "vcd")
head(Arthritis)
##   ID Treatment  Sex Age Improved
## 1 57   Treated Male  27     Some
## 2 46   Treated Male  29     None
## 3 77   Treated Male  30     None
## 4 17   Treated Male  32   Marked
## 5 36   Treated Male  46   Marked
## 6 23   Treated Male  58   Marked

변수 Treatment는 “Placebo”와 “Treated”를, Sex는 “Male”과 “Female”을, Improved는 “None”, “Some”, “Marked”을 범주로 갖고 있는 범주형 자료다.

\(\bullet\) 1차원 도수분포표 작성

1차원 도수분포표는 일변량 범주형 자료의 도수분포표를 의미한다.
함수 table()과 xtabs()로 변수 Improved의 1차원 도수분포표를 작성해 보자.

with(Arthritis, table(Improved))
## Improved
##   None   Some Marked 
##     42     14     28
xtabs(~ Improved, data = Arthritis)
## Improved
##   None   Some Marked 
##     42     14     28

우선 두 함수의 실행결과가 동일함을 알 수 있다. 사용법에서는 약간의 차이가 있는데, 함수 table() 안에는 벡터를 입력해야 하기 때문에, 함수 with()와 함께 사용하였다. 함수 xtabs() 안에는 R 공식으로 도수분포표 혹은 분할표의 형태를 정의하는데, 1차원 도수분포표의 경우는 ~ 표시 오른쪽에 해당 변수를 하나 입력하면 된다. 공식을 사용하여 모형을 정의하는 함수 안에는 데이터 프레임을 지정하여 사용할 수 있는 것이 일반적이다.

\(\bullet\) 1차원 상대도수분포표 작성

상대도수분포표는 함수 table() 또는 xtabs()로 작성된 table 객체를 함수 prop.table()에 입력하면 된다.

my_table1 <- with(Arthritis, table(Improved))
prop.table(my_table1)
## Improved
##      None      Some    Marked 
## 0.5000000 0.1666667 0.3333333

위의 결과에서 우리는 소수점 자릿수가 너무 길다는 문제를 발견할 수 있다. 소수점 자릿수의 조정은 함수 options()으로 할 수 있는데, 이 함수는 R의 전체적인 환경에 관련된 여러 옵션을 조정하는 가능을 갖고 있다. 이 중 출력되는 소수점 자릿수의 현재 값을 알아보는 방법과 수정하는 방법은 다음과 같다.

options("digits")
## $digits
## [1] 7
options("digits" = 2)

원래의 값은 소수점 이하 7자리까지 출력하는 것인데, 이것을 2자리로 수정하고 다시 변수 Improved의 상대도수분포표를 출력해 보자.

prop.table(my_table1)
## Improved
##   None   Some Marked 
##   0.50   0.17   0.33

\(\bullet\) 2차원 분할표 작성

1차원 도수분포표의 경우와 같이 2차원 분할표도 함수 table() 혹은 xtabs()로 작성할 수 있다. 변수 Improved와 Treatment의 2차원 분할표를 작성해 보자.

with(Arthritis, table(Treatment, Improved))
##          Improved
## Treatment None Some Marked
##   Placebo   29    7      7
##   Treated   13    7     21
xtabs(~ Treatment + Improved, data = Arthritis)
##          Improved
## Treatment None Some Marked
##   Placebo   29    7      7
##   Treated   13    7     21

함수 table()에서는 두 개의 변수가 콤마로 연결되고, 함수 xtabs()에서는 두 변수가 + 기호로 연결되는데, 두 경우 모두 첫 번째 변수가 분할표의 행 변수가 되고, 두 번째 변수가 열 변수가 된다.

\(\bullet\) 2차원 상대도수 분할표(결합분포) 작성

작성된 분할표를 함수 prop.table()에 입력하면 된다.

my_table2 <- with(Arthritis, table(Treatment, Improved))
prop.table(my_table2)
##          Improved
## Treatment  None  Some Marked
##   Placebo 0.345 0.083  0.083
##   Treated 0.155 0.083  0.250

위에서 options("digits" = 2)가 선언된 상태이지만 소수점 3자리까지 출력된 것을 볼 수 있다. 이것은 “digits”에 대한 함수 options()의 선언이 일종의 기댓값이기 때문이다.

\(\bullet\) 2차원 분할표의 한계분포(marginal distribution) 작성

2차원 분할표에서 한계분포를 작성하는 방법은 행 또는 열에 대한 합계를 구하는 것으로써, 함수 margin.table()로 작성할 수 있다. 사용법은 margin.table(x, margin = NULL)이다. x는 함수 table() 등으로 작성된 분할표나 행렬이 되고, margin은 1은 행, 2는 열을 지정하는 것인데,
실질적으로 이 함수는 apply(x,1, sum) 또는 apply(x,2, sum)과 동일한 작업을 수행한다. margin에 아무것도 지정하지 않으면 sum(x)를 출력한다.

변수 Improved와 Treatment의 2차원 분할표인 my_table2를 대상으로 한계분포표를 작성해 보자. margin.table(my_table2, 1)은 행 방향으로 합계를 구하는 것이므로 행 변수 Treatment의 도수분포표, 즉 한계분포표가 작성된다. margin.table(my_table2, 2)는 열 방향의 합계를 구하는 것으로 열 변수 Improved의 한계분포표가 작성된다. margin.table(my_table2)는 margin에 아무것도 지정하지 않은 것으로 이 경우에는 관찰값의 총 개수가 계산된다.

my_table2
##          Improved
## Treatment None Some Marked
##   Placebo   29    7      7
##   Treated   13    7     21
margin.table(my_table2, 1)
## Treatment
## Placebo Treated 
##      43      41
margin.table(my_table2, 2)
## Improved
##   None   Some Marked 
##     42     14     28
margin.table(my_table2)
## [1] 84

한계분포표를 상대도수로 표현하려면 함수 margin.table()의 결과를 prop.table()에 입력하면 된다.

prop.table(margin.table(my_table2, 1))
## Treatment
## Placebo Treated 
##    0.51    0.49

위 연산 방식은 함수 안에 다른 함수를 입력하는 방식인데, 이것보다 더 효율적인 방식은 pipe 연산자를 이용하는 것이다. Pipe 연산자는 tidyverse 생태계에서 사용되는 magrittr의 |>가 있지만, base R에도 |>가 있다. 두 pipe 연산자의 기본적인 사용법은 lhs |> rhs와 lhs |> rhs으로 동일하다. 차이점은 lhs가 rhs의 첫 번째 변수가 아닌 경우에 대한 위치 지정 기호이다. 예를 들어, f(y, x)를 표현할 때 |> 연산자의 경우에는 .을 사용해서 x |> f(y, .)라고 하지만, |>의 경우에는 _를 사용해서 x |> f(y, _)라고 한다.

my_table2 |>
  margin.table(1) |>
  prop.table()
## Treatment
## Placebo Treated 
##    0.51    0.49

2차원 분할표에 한계분포표를 추가하려면 함수 addmargins()를 사용하면 된다.

my_table2 |>
  addmargins()
##          Improved
## Treatment None Some Marked Sum
##   Placebo   29    7      7  43
##   Treated   13    7     21  41
##   Sum       42   14     28  84
my_table2 |>
  prop.table() |>
  addmargins()
##          Improved
## Treatment  None  Some Marked   Sum
##   Placebo 0.345 0.083  0.083 0.512
##   Treated 0.155 0.083  0.250 0.488
##   Sum     0.500 0.167  0.333 1.000

행 또는 열 변수 중 한 변수의 한계분포만을 추가하려면 함수 addmargins()에 margin에 관련된 숫자를 지정하면 된다. 함수 addmargins()에 margin = 1이 입력되면 행에 한계분포가 추가되고, margin = 2가 입력되면 열에 한계분포가 추가된다.

my_table2 |>
  prop.table() |>
  addmargins(1)
##          Improved
## Treatment  None  Some Marked
##   Placebo 0.345 0.083  0.083
##   Treated 0.155 0.083  0.250
##   Sum     0.500 0.167  0.333
my_table2 |>
  prop.table() |>
  addmargins(2)
##          Improved
## Treatment  None  Some Marked   Sum
##   Placebo 0.345 0.083  0.083 0.512
##   Treated 0.155 0.083  0.250 0.488

\(\bullet\) 조건분포 작성

조건분포는 함수 prop.table()에 margin을 지정함으로써 작성할 수 있다. 두 범주형 변수의 관계가 반응변수와 설명변수로 설정되어 있는 경우에는 결합분포인 2차원 상대도수 분할표보다 두 변수 사이의 관계를 규명하는 데 더 도움이 된다. 조건 변수를 행 변수로 할 것인지 혹은 열 변수로 할 것인지는 함수 prop.table()의 옵션 margin에 1 또는 2 중 하나를 선택하면 된다.

my_table2 |>
  prop.table(1)
##          Improved
## Treatment None Some Marked
##   Placebo 0.67 0.16   0.16
##   Treated 0.32 0.17   0.51
my_table2 |>
  prop.table(2)
##          Improved
## Treatment None Some Marked
##   Placebo 0.69 0.50   0.25
##   Treated 0.31 0.50   0.75

옵션 margin에 1을 입력한 첫 번째 경우는 행 변수 Treatment가 조건변수가 되어, 위약 처리한 Placebo에서는 16%의 환자에게서 큰 진전이 있었지만 새로운 처리방법으로 처리된 Treated에서는 51%의 환자에게서 큰 진전이 있었다는 것을 알 수 있다.

옵션 margin에 2를 입력한 두 번째 경우는 열 변수 Improved가 조건변수가 된 경우로 병세가 많이 호전된 Marked 그룹 중에 75%의 환자들이 Treated 그룹에 속한다는 것도 알 수 있다.

\(\bullet\) 분할표에서 결측값 처리

함수 table()은 자료에 포함된 NA 값을 무시하고 분할표를 작성하는 것이 디폴트이다. 만일 NA의 빈도수를 분할표에 나타내려면 옵션 useNA = “ifany”를 추가하면 된다.

예를 들어 데이터 프레임 airquality에서 변수 Ozone의 값이 80이 넘는 날짜가 며칠이나 되는지 월별로 나타내는 분할표를 작성해 보자.

with(airquality, table(OzHi = Ozone > 80, Month))
##        Month
## OzHi     5  6  7  8  9
##   FALSE 25  9 20 19 27
##   TRUE   1  0  6  7  2

위의 분할표를 보면 5월은 26일, 6월은 9일밖에 없는 등 많은 날짜가 생략되어 있음을 알 수 있다. 이것은 자료에 NA가 있기 때문이며 이것을 모두 포함시키려면 다음과 같이 실행하면 된다.

with(airquality, table(OzHi = Ozone > 80, Month, useNA = "ifany"))
##        Month
## OzHi     5  6  7  8  9
##   FALSE 25  9 20 19 27
##   TRUE   1  0  6  7  2
##   <NA>   5 21  5  5  1

\(\bullet\) SAS 또는 SPSS에서 출력되는 형태의 분할표 얻기

SAS의 PROC FREQ나 SPSS의 CROSSTABS의 실행결과와 비슷한 형태의 분할표를 얻고자 한다면 패키지 gmodels의 함수 CrossTable()을 사용하면 된다.

library(gmodels)
with(Arthritis, CrossTable(Treatment, Improved))
## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## | Chi-square contribution |
## |           N / Row Total |
## |           N / Col Total |
## |         N / Table Total |
## |-------------------------|
## 
##  
## Total Observations in Table:  84 
## 
##  
##              | Improved 
##    Treatment |      None |      Some |    Marked | Row Total | 
## -------------|-----------|-----------|-----------|-----------|
##      Placebo |        29 |         7 |         7 |        43 | 
##              |     2.616 |     0.004 |     3.752 |           | 
##              |     0.674 |     0.163 |     0.163 |     0.512 | 
##              |     0.690 |     0.500 |     0.250 |           | 
##              |     0.345 |     0.083 |     0.083 |           | 
## -------------|-----------|-----------|-----------|-----------|
##      Treated |        13 |         7 |        21 |        41 | 
##              |     2.744 |     0.004 |     3.935 |           | 
##              |     0.317 |     0.171 |     0.512 |     0.488 | 
##              |     0.310 |     0.500 |     0.750 |           | 
##              |     0.155 |     0.083 |     0.250 |           | 
## -------------|-----------|-----------|-----------|-----------|
## Column Total |        42 |        14 |        28 |        84 | 
##              |     0.500 |     0.167 |     0.333 |           | 
## -------------|-----------|-----------|-----------|-----------|
## 
##

위 결과는 SAS 결과물 형태로 출력된 것이며 SPSS 결과물 형태로 출력하고자 한다면 옵션 format = “SPSS”을 추가하면 된다. 자료의 도수와 기대도수만을 나타내고, 두 변수의 독립성 검정을 하고자 한다면 옵션 prop.r, prop.c, prop.t, prop.chisq에 FALSE를 지정하고, expected = TRUE와 chisq = TRUE를 추가하면 된다.

with(Arthritis, CrossTable(Treatment, Improved, 
                           prop.r = FALSE, prop.c = FALSE, prop.t = FALSE,
                           prop.chisq = FALSE, expected = TRUE, chisq = TRUE)
     )
## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |              Expected N |
## |-------------------------|
## 
##  
## Total Observations in Table:  84 
## 
##  
##              | Improved 
##    Treatment |      None |      Some |    Marked | Row Total | 
## -------------|-----------|-----------|-----------|-----------|
##      Placebo |        29 |         7 |         7 |        43 | 
##              |    21.500 |     7.167 |    14.333 |           | 
## -------------|-----------|-----------|-----------|-----------|
##      Treated |        13 |         7 |        21 |        41 | 
##              |    20.500 |     6.833 |    13.667 |           | 
## -------------|-----------|-----------|-----------|-----------|
## Column Total |        42 |        14 |        28 |        84 | 
## -------------|-----------|-----------|-----------|-----------|
## 
##  
## Statistics for All Table Factors
## 
## 
## Pearson's Chi-squared test 
## ------------------------------------------------------------
## Chi^2 =  13     d.f. =  2     p =  0.0015 
## 
## 
##

9.2.2 이변량 및 다변량 범주형 자료를 위한 그래프

이변량 범주형 자료를 대상으로 그래프를 작성하는 주된 목적은 두 범주형 변수의 관계를 탐색하는 것이다. 많이 사용되는 그래프는 막대 그래프이며, 이변량의 경우 쌓아 올린 형태의 막대 그래프와 옆으로 붙여 놓은 형태의 막대 그래프가 사용된다.

패키지 ggplot2에서는 함수는 geom_bar()가 두 형태의 그래프를 작성할 수 있다. 또한 이변량 및 다변량 범주형 자료의 관계 탐색에 적합한 그래프로써 mosaic plot이 있는데, 이 그래프는 패키지 vcd의 mosaic()으로 작성할 수 있다.

예제로 패키지 vcd의 데이터 프레임 Arthritis의 변수 Treatment와 Improved의 관계 탐색을 위한 그래프를 작성해 보자. 우선 함수 count()로 두 변수의 분할표를 작성해 보자.

data(Arthritis, package = "vcd")
Arthritis |> 
  count(Treatment, Improved)
##   Treatment Improved  n
## 1   Placebo     None 29
## 2   Placebo     Some  7
## 3   Placebo   Marked  7
## 4   Treated     None 13
## 5   Treated     Some  7
## 6   Treated   Marked 21

\(\bullet\) 쌓아 올린 막대그래프

쌓아 올린 막대그래프를 작성할 때 주의할 점은 행 변수와 열 변수 중 어느 변수를 위주로 막대를 쌓아 올릴 것인지를 결정해야 한다는 것이다. 만일 두 변수가 설명변수와 반응변수의 성격을 갖고 있다면, 설명변수를 위주로 막대를 쌓는 것이 두 변수의 관계 탐색에 더 효과적일 것이다. 데이터 프레임 Arthritis의 경우에는 변수 Improved가 반응변수이고 나머지 변수는 모두 설명변수가 되기 때문에 변수 Treatment를 위주로 쌓아 올린 막대그래프를 작성해 보자.

함수 geom_bar()에서 시각적 요소 x에는 설명변수를, 시각적 요소 fill에는 반응변수를 연결하면, 설명변수를 위주로 쌓아 올린 막대그래프를 작성할 수 있다. 위약 그룹과 실제 치료가 이루어진 그룹 안에서 병세 호전 정도의 분포를 확인할 수 있으며, 두 그룹 사이에 병세 호전 정도의 차이를 확인할 수 있는 그래프이다.

library(tidyverse)
Arthritis |> 
  ggplot(aes(x = Treatment, fill = Improved)) +
  geom_bar() +
  ylab(NULL)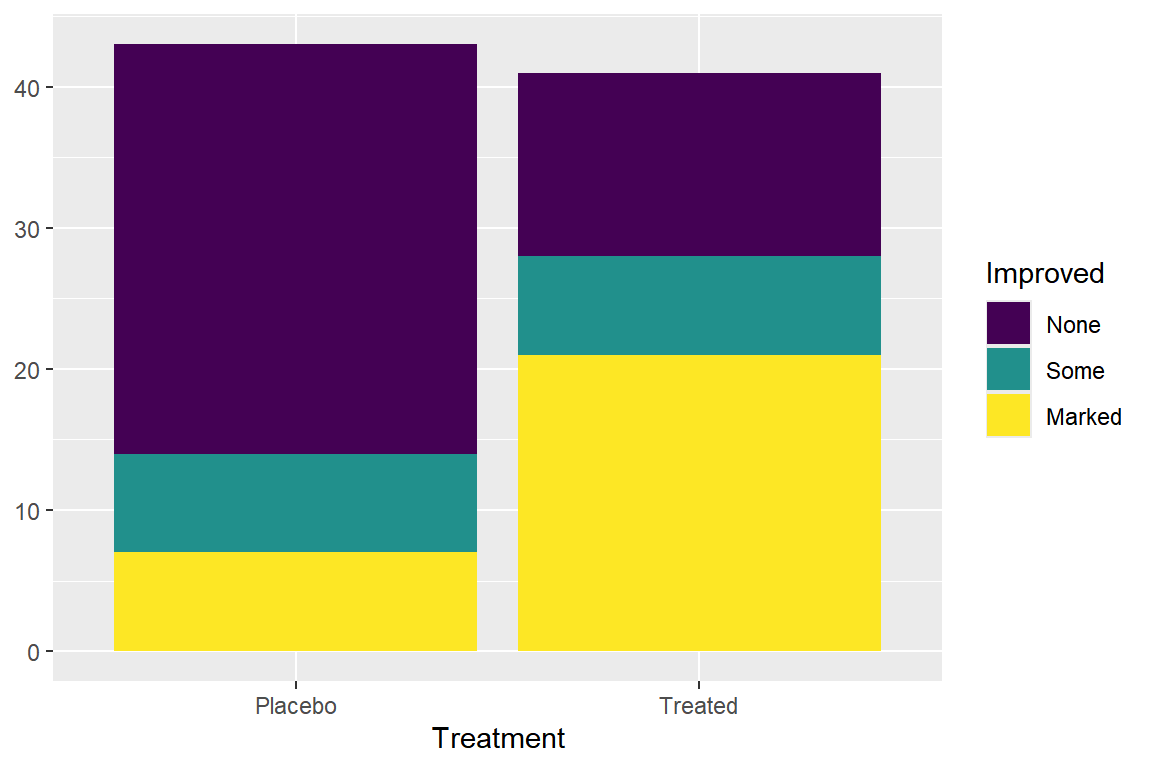
쌓아 올린 막대그래프

그림 9.11: 쌓아 올린 막대그래프

두 변수의 분할표를 데이터로 사용하여 쌓아 올린 막대그래프를 작성해야 하는 경우에는 분할표를 데이터 프레임 형태로 생성시키고, 설명변수인 Treatment를 x에, 빈도수인 n를 y에, 반응변수인 Improved를 fill에 매핑하고, 함수 geom_col() 또는 geom_bar(stat = ”identity”)를 사용하면 된다.

Arthritis |> 
  count(Treatment, Improved) |> 
  ggplot(aes(x = Treatment, y = n, fill = Improved)) +
  geom_col() +
  ylab(NULL)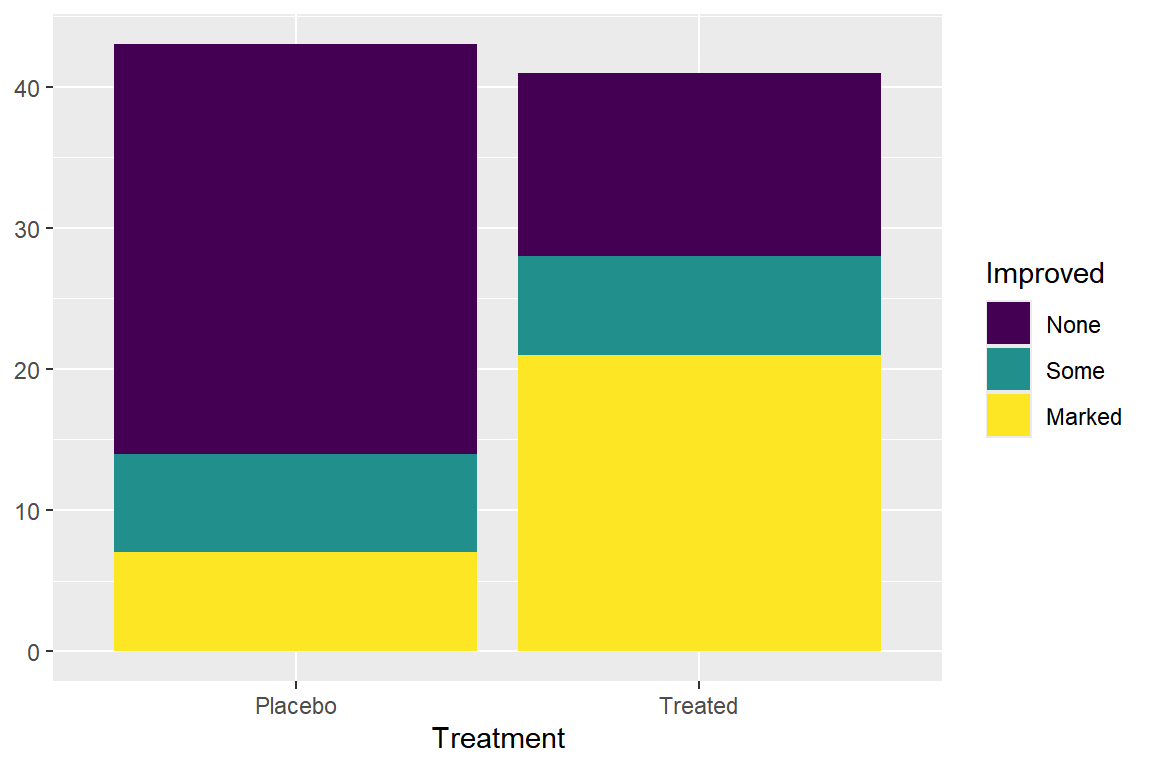
쌓아 올린 막대그래프

그림 9.12: 쌓아 올린 막대그래프

\(\bullet\) 옆으로 붙여 놓은 막대그래프

옆으로 붙여 놓은 막대 그래프를 작성하기 위해서는 함수 geom_bar()의 변수 position에 “dodge” 혹은 “dodge2”를 지정하면 된다. “dodge2”는 막대 폭을 조금 줄여서 막대 사이에 약간의 빈틈을 만들어 주는 차이가 있다.

Arthritis |> 
  ggplot(aes(x = Treatment, fill = Improved)) +
  geom_bar(position = "dodge") +
  ylab(NULL)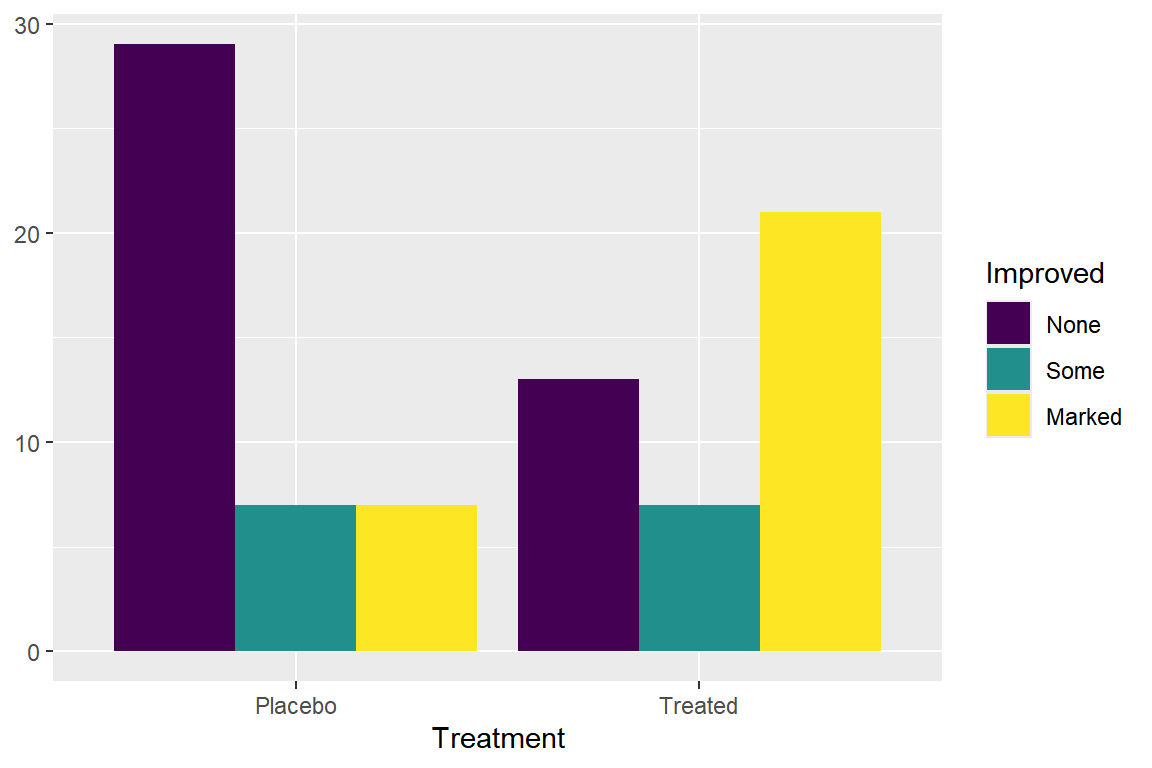
옆으로 붙여 놓은 막대그래프

그림 9.13: 옆으로 붙여 놓은 막대그래프 

Arthritis |> 
  ggplot(aes(x = Treatment, fill = Improved)) +
  geom_bar(position = "dodge2") +
  ylab(NULL)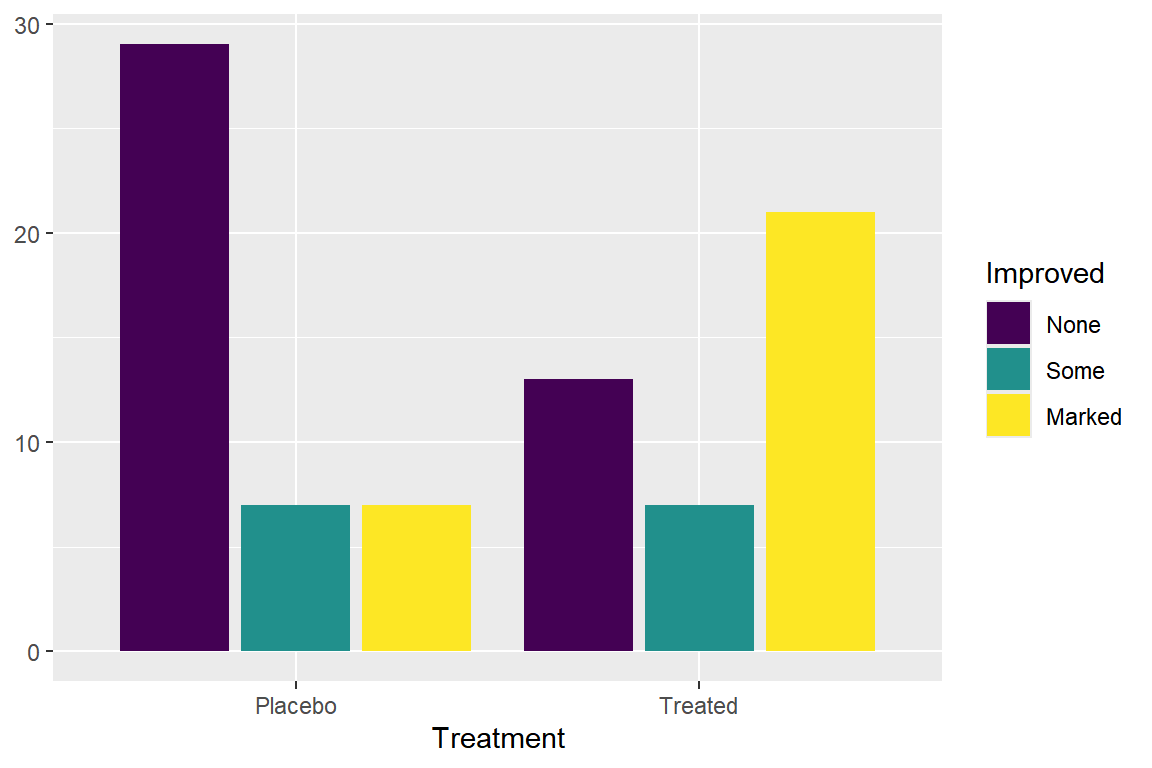
옆으로 붙여 놓은 막대그래프

그림 9.14: 옆으로 붙여 놓은 막대그래프

두 변수의 분할표를 데이터로 사용하여 옆으로 붙여 놓은 막대그래프를 작성해 보자.

Arthritis |> 
  count(Treatment, Improved) |> 
  ggplot(aes(x = Treatment, y = n, fill = Improved)) +
  geom_col(position = "dodge") +
  ylab(NULL)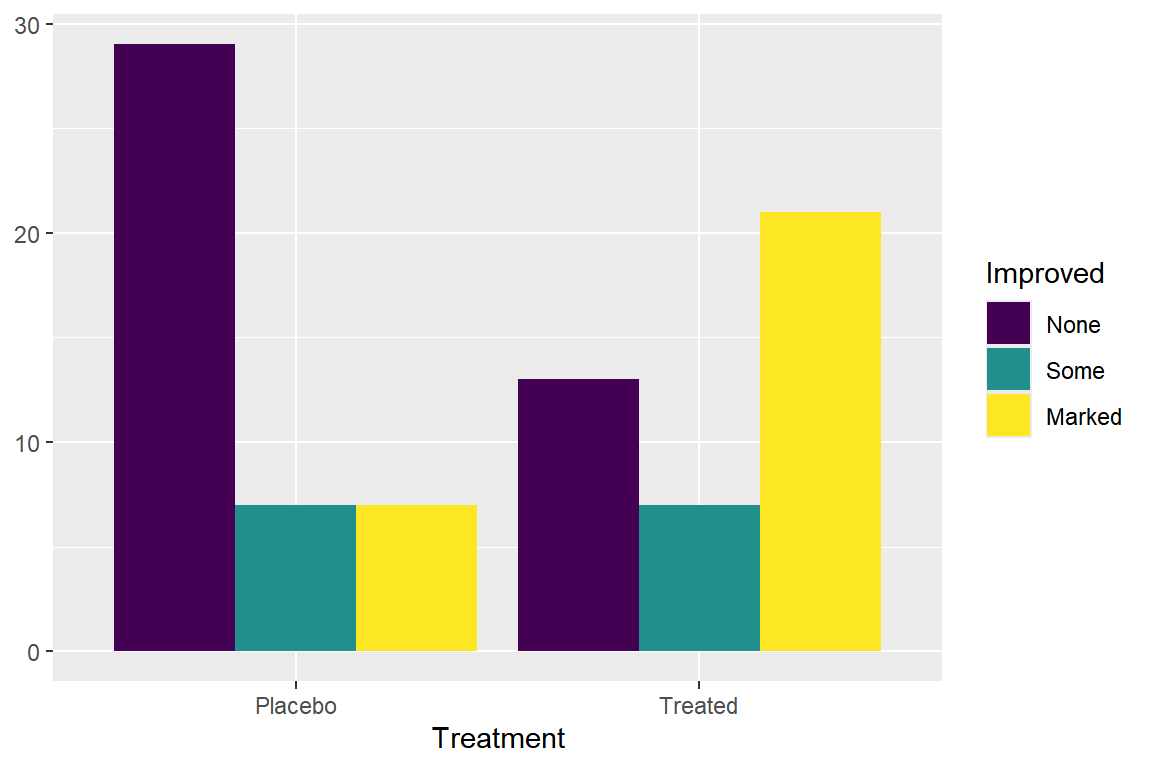
옆으로 붙여 놓은 막대그래프

그림 9.15: 옆으로 붙여 놓은 막대그래프

상대도수를 사용하여 옆으로 붙여 놓은 막대 그래프를 작성해 보자. 먼저 함수 geom_bar()와 함수 facet_wrap()을 추가로 사용한 방법이다.

Arthritis |> 
  ggplot(aes(x = Improved, y = after_stat(prop), group = 1)) +
  geom_bar() +
  facet_wrap(vars(Treatment)) +
  ylab(NULL)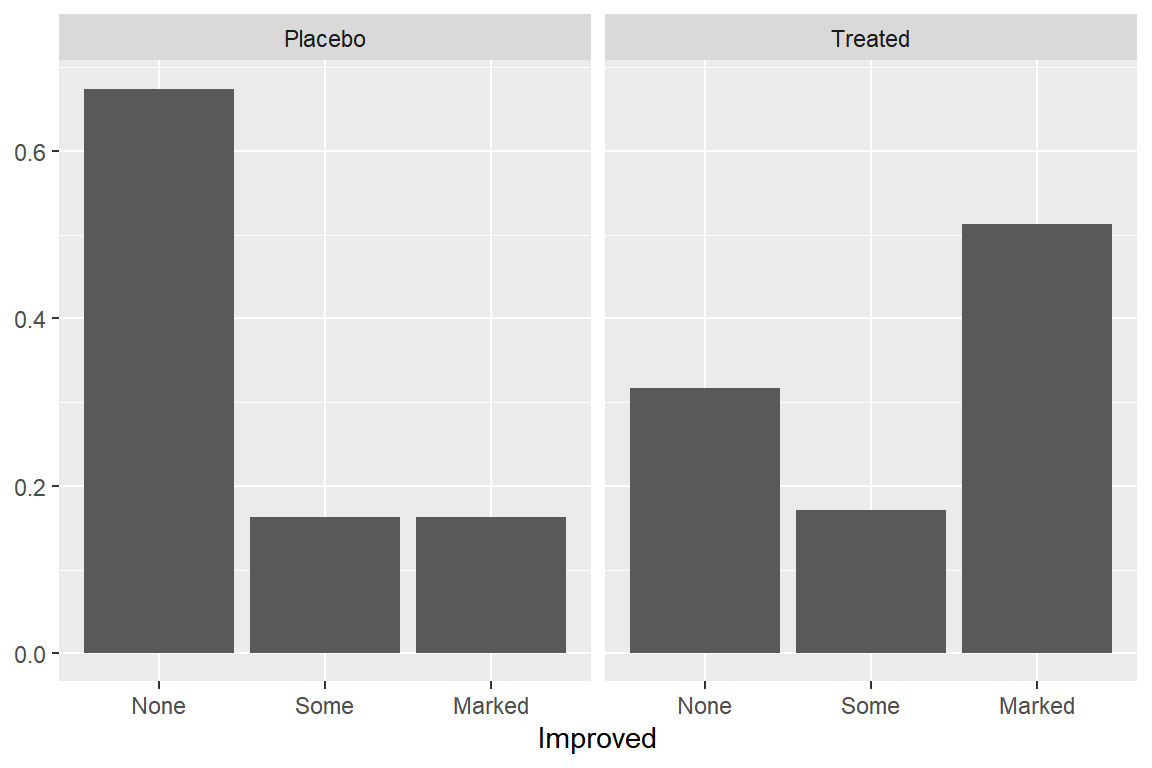
상대도수에 의한 옆으로 붙여 놓은 막대 그래프

그림 9.16: 상대도수에 의한 옆으로 붙여 놓은 막대 그래프

상대도수를 사용자가 직접 계산해서 함수 geom_col()을 사용한 방법이다.

Arthritis |> 
  count(Treatment, Improved) |> 
  mutate(prop = n/sum(n)) |> 
  ggplot(aes(x = Treatment, y = prop, fill = Improved)) +
  geom_col(position = "dodge2") + ylab(NULL)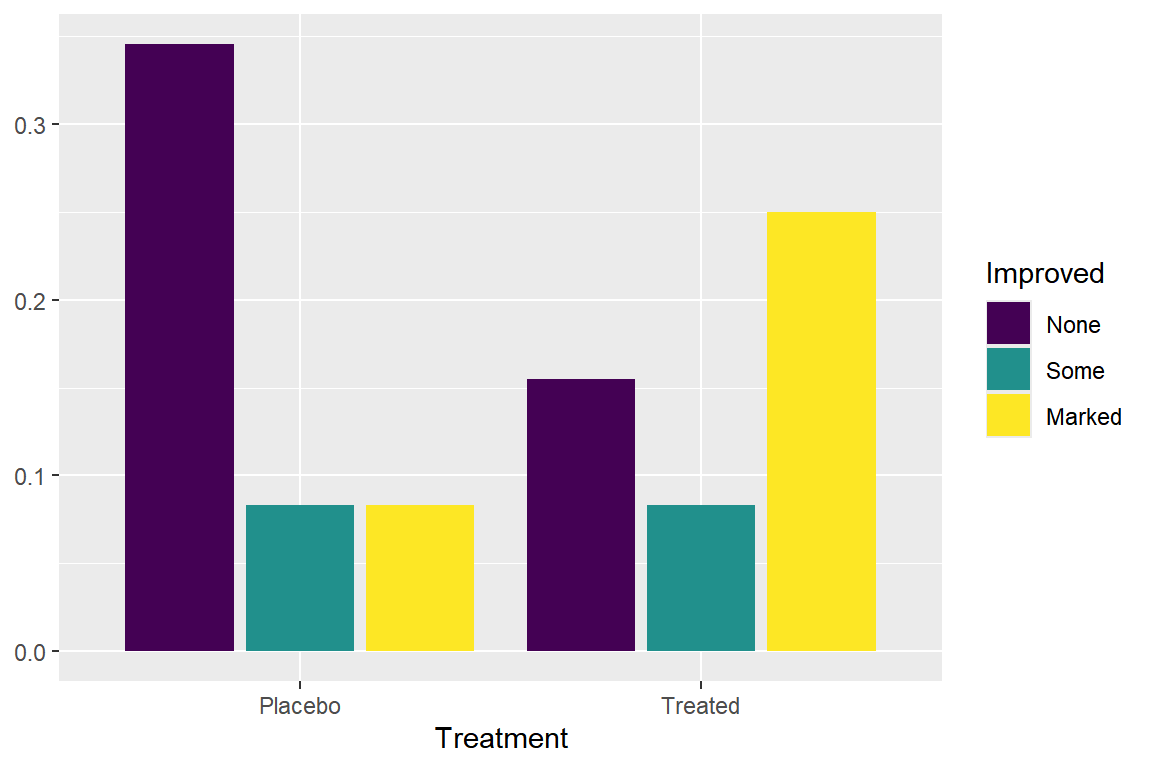
상대도수에 의한 옆으로 붙여 놓은 막대 그래프

그림 9.17: 상대도수에 의한 옆으로 붙여 놓은 막대 그래프

함수 geom_bar()로 두 변수의 막대그래프를 작성하는 경우, 시각적 요소 x와 fill에 각각 동일한 변수를 매핑하여도 position에 어떤 값을 지정하는가에 따라 다른 형태의 막대그래프가 작성된다. 디폴트는 “stack”으로 쌓아 올린 형태가 되고, “dodge”는 옆으로 붙여 놓은 형태가 됨을 알 수 있었다. 또 다른 가능한 다른 값으로 “fill”이 있는데, 이 경우에는 x 변수에 대한 fill 변수의 조건부 확률로 막대그래프가 각각 작성된다. 따라서 각 막대의 높이는 1이 된다.

Arthritis |> 
  ggplot(aes(x = Treatment, fill = Improved)) +
  geom_bar(position = "fill") +
  ylab(NULL)
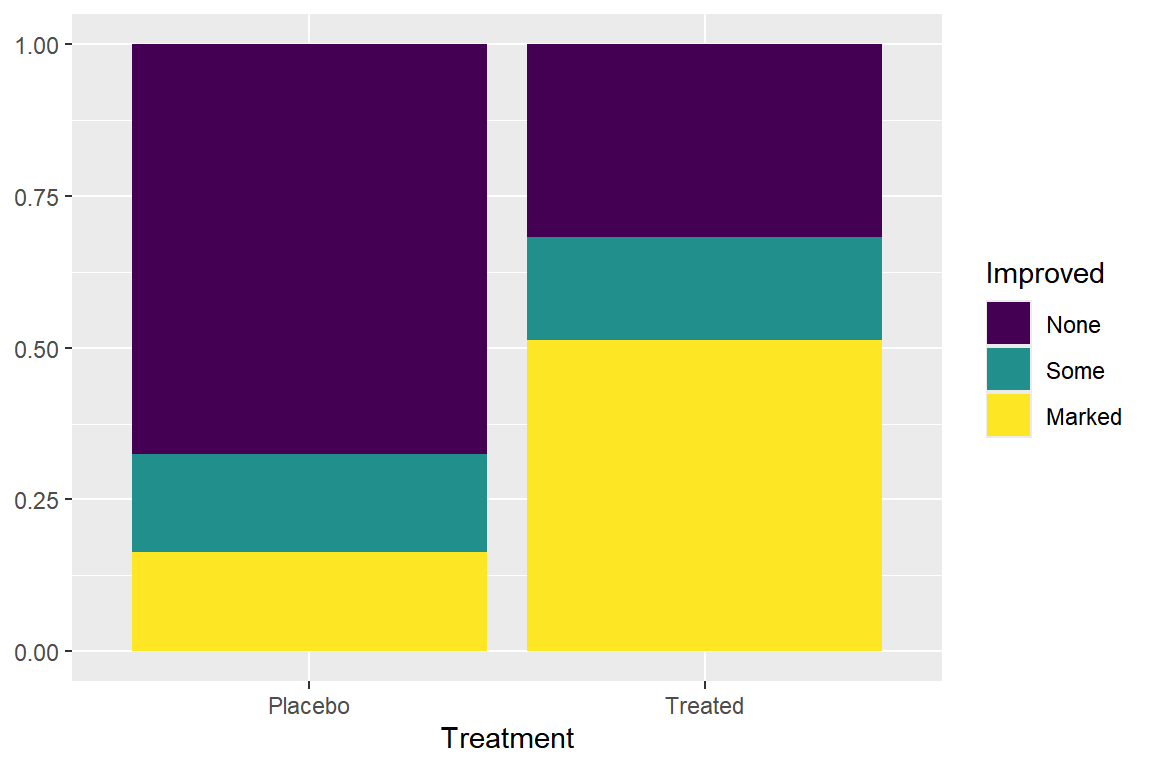
조건부 확률을 표현한 쌓아 올린 막대그래프

그림 9.18: 조건부 확률을 표현한 쌓아 올린 막대그래프

그림 9.18 에서 각 조각의 면적은 행 변수인 Treatment를 조건으로 하는 열 변수 Improved의 조건부 확률에 의하여 결정됨을 다음의 분할표와 비교해 보면 알 수 있다. 설명변수와 반응변수 사이의 관계를 파악하는 데 더 적합하다고 할 수 있다.

Arthritis |> 
    group_by(Treatment, Improved) |> 
    tally() |> 
    mutate(prop = n/sum(n))
## # A tibble: 6 × 4
## # Groups:   Treatment [2]
##   Treatment Improved     n  prop
##   <fct>     <ord>    <int> <dbl>
## 1 Placebo   None        29 0.674
## 2 Placebo   Some         7 0.163
## 3 Placebo   Marked       7 0.163
## 4 Treated   None        13 0.317
## 5 Treated   Some         7 0.171
## 6 Treated   Marked      21 0.512

\(\bullet\) Mosaic plot

이변량 혹은 다변량 범주형 변수의 관계를 탐색할 때 유용하게 사용되는 그래프가 mosaic plot이다. 이 그래프는 쌓아 올린 막대그래프를 확장한 그래프라고 할 수 있으며, 패키지 vcd의 함수 mosaic()으로 작성할 수 있다.

데이터 프레임 Arthritis의 변수 Treatment와 Improved의 분할표인 객체 my_table을 사용하여 작성해 보자.

my_table <- with(Arthritis, table(Treatment, Improved))
library(vcd)
mosaic(my_table, direction = "v")
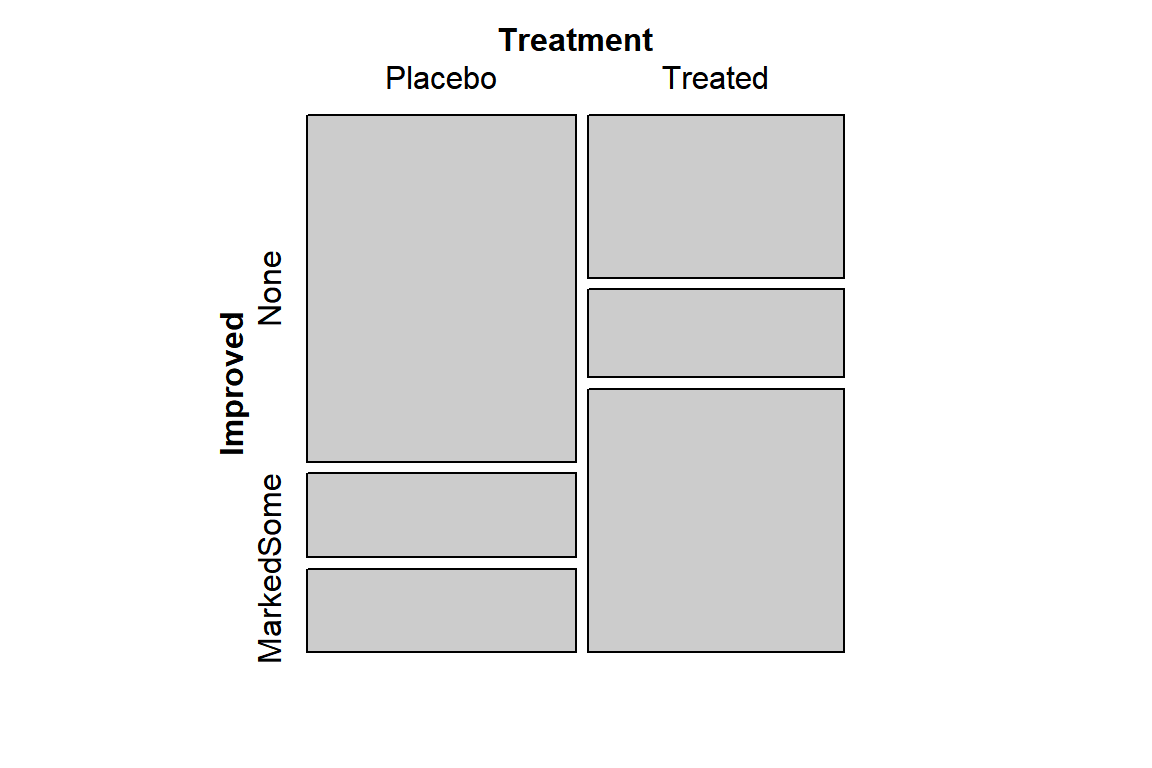
Mosaic plot

그림 9.19: Mosaic plot

작성방법은 두 변수의 분할표 행 변수(Treatment)의 상대도수(Placebo 0.512, Treated 0.488)의 비율에 따라 정사각형을 수직(direction = “v”)으로 분리한다. 이어서 수직으로 분리된 두 조각을 행 변수 Treatment를 조건으로 하는 열 변수 Improved의 조건부 확률에 비례하여 수평방향으로 각각 분리하여 작성한다. 옵션 direction = “v”가 생략되면 첫번째 분할은 수평방향(direction = “h”)으로 이루어지고, 따라서 두 번째 분할은 수직으로 이루어진다.

함수 mosaic()은 R 공식 형태로도 변수를 지정할 수 있다. 만일 ~ 기호의 오른쪽에만 mosaic(~ var1 + var2)의 형태로 변수를 입력을 하면 var1이 첫 번째 분할 변수, var2가 두 번째 분할 변수로 사용된다. 또한 mosaic(var1 ~ var2)의 형태로 입력되면 var1이 반응변수, var2가 설명변수로 지정되는 것이며, 설명변수가 먼저 분할 변수로 사용되고 마지막으로 반응변수가 분할 변수로 사용된다. 또한 반응변수의 수준에 따라 각 조각이 다른 색으로 채워진다.

mosaic(Improved ~ Treatment, data = Arthritis, direction = "v")
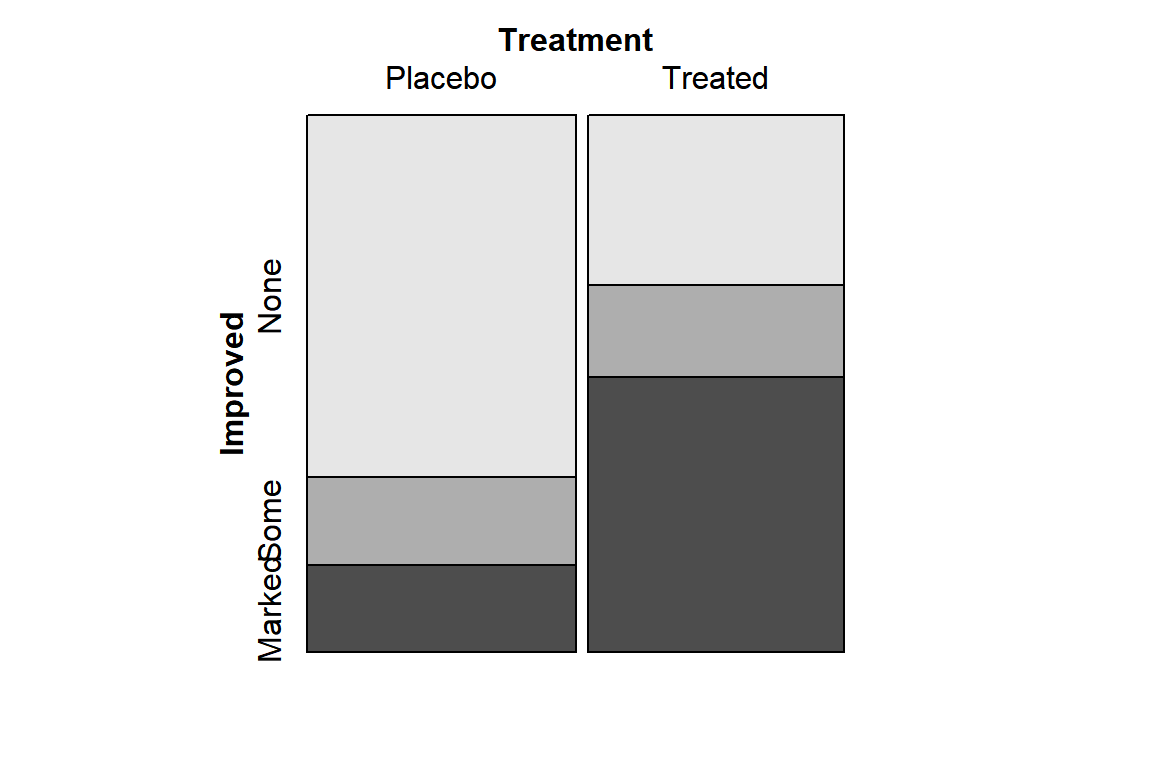
Mosaic plot

그림 9.20: Mosaic plot

이번에는 반응변수 Improved와 설명변수 Treatment, Sex의 관계를 mosaic plot으로 나타내 보자.

mosaic(Improved ~ Treatment + Sex, data = Arthritis, direction = "v")
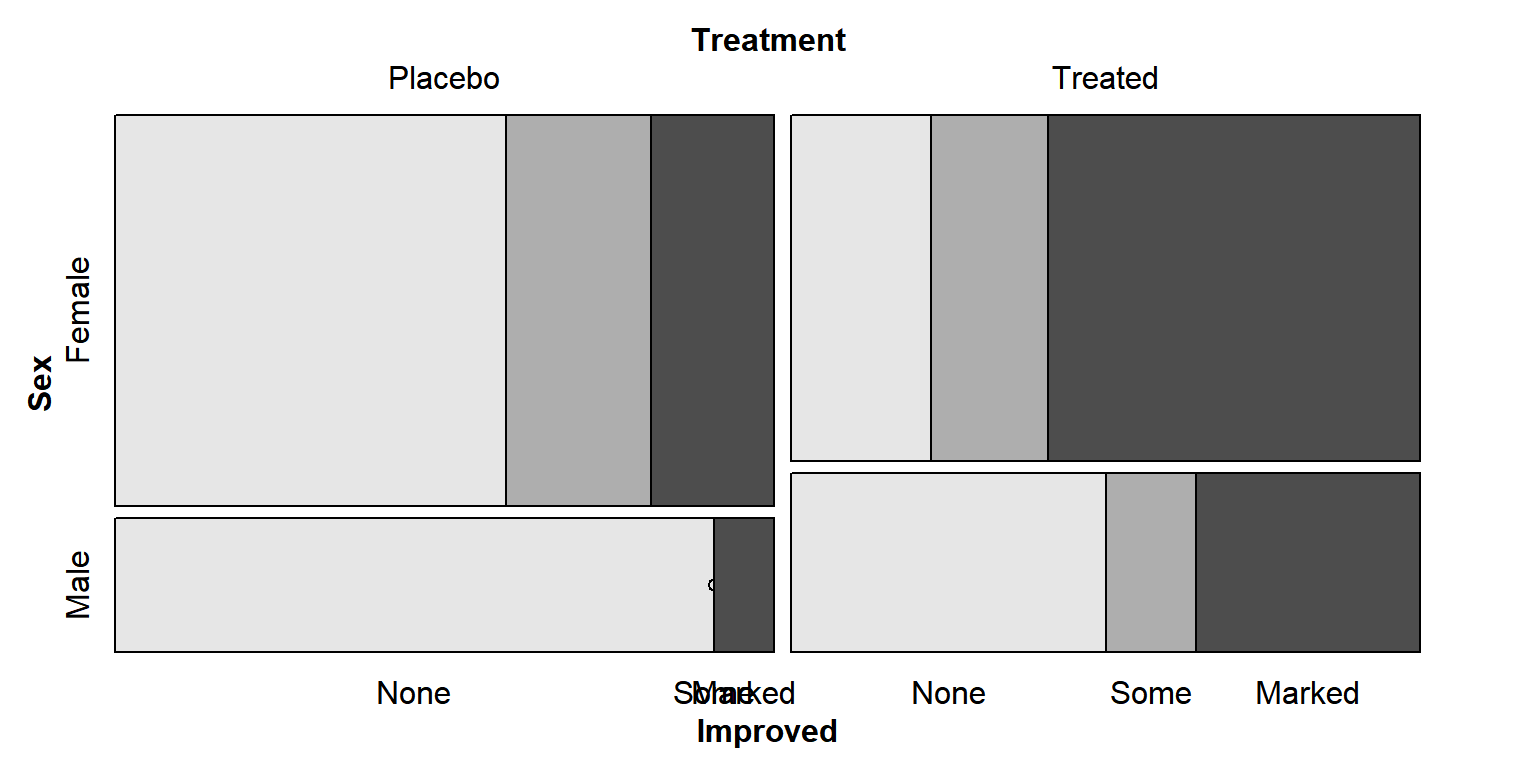
세 변수의 mosaic plot

그림 9.21: 세 변수의 mosaic plot

함수 mosaic()에서 선의 종류나 색 등의 그래픽 모수는 패키지 grid를 통해 조절이 된다. 패키지 grid에서 그래픽 모수의 기본적인 설정은 gp = gpar(...)이 되며, 다각형도형을 색으로 채우는 옵션은 fill이 된다.

mosaic(Improved ~ Treatment + Sex, data = Arthritis, direction = "v", 
       gp = gpar(fill = c("pink", "rosybrown", "steelblue")))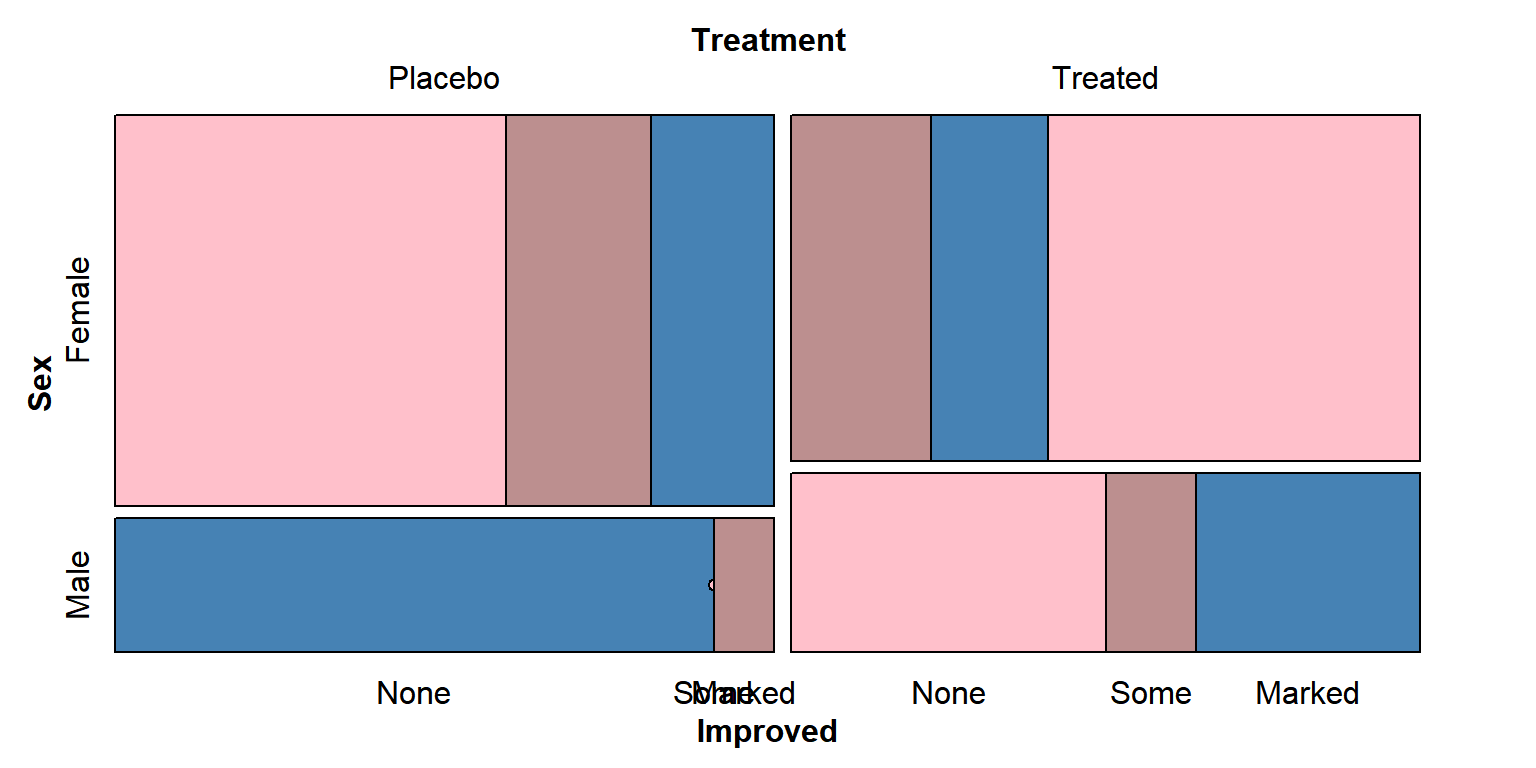
세 변수의 mosaic plot

그림 9.22: 세 변수의 mosaic plot

그림 9.21 에서 확인할 수 있는 또 다른 사항은 Treatment가 Placebo이고, Sex가 Male인 그룹에서 Improved가 Some에 해당하는 부분에 점이 찍혀있는 것이다. 그것은 이 그룹에 해당되는 자료가 없기 때문인데, 이때 사용되는 점의 크기는 옵션 zero_size로 조절할 수 있다.

Mosaic plot을 포함한 범주형 자료의 시각화와 관련된 다양한 방법에 대해서는 Michael Friendly의 홈페이지 를 참조하기 바란다.

9.3 일변량 연속형 자료 탐색

일변량 연속형 자료에 대해서 우리가 가장 관심을 갖고 있는 정보는 자료의 분포 형태일 것이다. 자료의 중심은 어디인가? 자료의 퍼짐 정도는 어떠한가? 이러한 질문에 효과적인 답을 얻기 위해서는 적절한 그래프를 잘 선택해야 할 것이다.

9.3.1 줄기-잎 그림

줄기-잎 그림은 비교적 소규모 자료의 분포를 나타내는 데 적합한 그래프라고 할 수 있다. 자료를 ’줄기’와 ’잎’으로 구분하고, ’줄기’를 수직으로 세운 후에 해당되는 ’줄기’에 ’잎’들을 크기 순서로 붙여 나타내는 그림이다. 줄기-잎 그림은 함수 stem()으로 작성할 수 있으며, 일반적인 사용법은 stem(x, scale = 1)이다. 변수 x는 숫자형 벡터이며, scale은 줄기-잎 그림의 길이를 조절하는 것으로 scale = 2가 되면 대략 2배 길이의 그래프가 그려진다. 그래프의 길이를 늘이는 방법은 대부분 ’줄기’를 더 세분화시키는 방식으로 이루어진다.

예제 데이터로는 데이터 프레임 women을 사용해 보자. 여기에는 30세에서 39세 사이의 미국 여성들의 키와 몸무게 데이터가 height와 weight로 입력되어 있다. 두 변수의 줄기-잎 그림을 그려보자. 줄기-잎 그림은 Console 창에 결과가 나타난다.

with(women, stem(height))
## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##   5 | 89
##   6 | 01234
##   6 | 56789
##   7 | 012
with(women, stem(weight))
## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##   11 | 57
##   12 | 0369
##   13 | 259
##   14 | 26
##   15 | 049
##   16 | 4

옵션 scale을 이용하여 그래프의 길이를 늘여야 하는 경우에 대한 예제를 살펴보자.

x <- c(98, 102, 114, 122, 132, 144, 106, 117, 151, 118, 124, 115)
stem(x)
## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##    8 | 8
##   10 | 264578
##   12 | 242
##   14 | 41

자료의 개수에 비해 ’줄기’가 지나치게 많은 경우로, 디폴트 scale 값에서는 ’줄기’가 통합되어 실제로는 없는 줄기가 나타났다. 이것을 scale = 2로 조정하여 작성해 보자.

stem(x, scale = 2)
## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##    9 | 8
##   10 | 26
##   11 | 4578
##   12 | 24
##   13 | 2
##   14 | 4
##   15 | 1

9.3.2 상자그림

상자그림은 box plot 혹은 box-and-whiskers plot이라고 불리는 그래프로 John Tukey가 개발하였다. 사분위수인 0.25분위수(Q1), 중앙값, 0.75분위수(Q3)를 이용하여 작성하는 단순한 형태의 그래프이나, 분포의 중심, 퍼짐 정도, 치우침 정도(skewness), 꼬리의 길이 등이 상당히 명확하게 나타난다.

상자그림의 작성에서 0.25분위수, 중앙값, 그리고 0.75분위수로 표현되는 상자로부터 양쪽 꼬리 방향으로 그려지는 whisker의 길이에 대한 두 가지 대안이 있는데, 첫 번째 방법은 최솟값과 최댓값까지 단순하게 연결하는 것이다. 두 번째 방법은 상자의 길이(IQR)의 1.5배가 넘지 않는 관찰값까지 연결하고, 그 범위를 초과하는 관찰값들은 따로 점으로 표시하는 방법이다. 첫 번째 방법은 꼬리 부분에 있을 수 있는 이상값에 대한 정보를 전혀 표현할 수 없기 때문에 최근에는 거의 사용되지 않는 방법이라 하겠다. 따라서 두 번째 방법으로만 상자그림을 작성하겠다.

예제 데이터로는 패키지 UsingR에 있는 데이터 프레임 alltime.movies를 사용해 보자. 데이터 프레임 alltime.movies에는 2003년까지 미국에서 상영된 영화 중 총수입이 가장 많았던 79개 영화의 총수입(Gross)과 처음 상영된 년도(Release.Year)가 변수로 있고, 영화제목은 행 이름으로 입력되어 있다. 총수입 Gross의 상자그림을 작성해 보자.

상자그림은 함수 geom_boxplot()으로 작성할 수 있다. 한 변수의 상자그림을 작성하는 경우에도 시각적 요소 x와 y가 모두 필요하다. x에 하나의 값만을 갖는 문자를 매핑하고, y에 연속형 변수를 매핑하면 수직방향으로 상자그림이 작성되고, x에 연속형 변수를, y에 하나의 값을 갖는 문자를 매핑하면 수평방향으로 상자그림이 작성된다.

data(alltime.movies, package = "UsingR")
library(tidyverse)
ggplot(alltime.movies, aes(x = "", y = Gross)) + 
  geom_boxplot() +
  xlab(NULL)
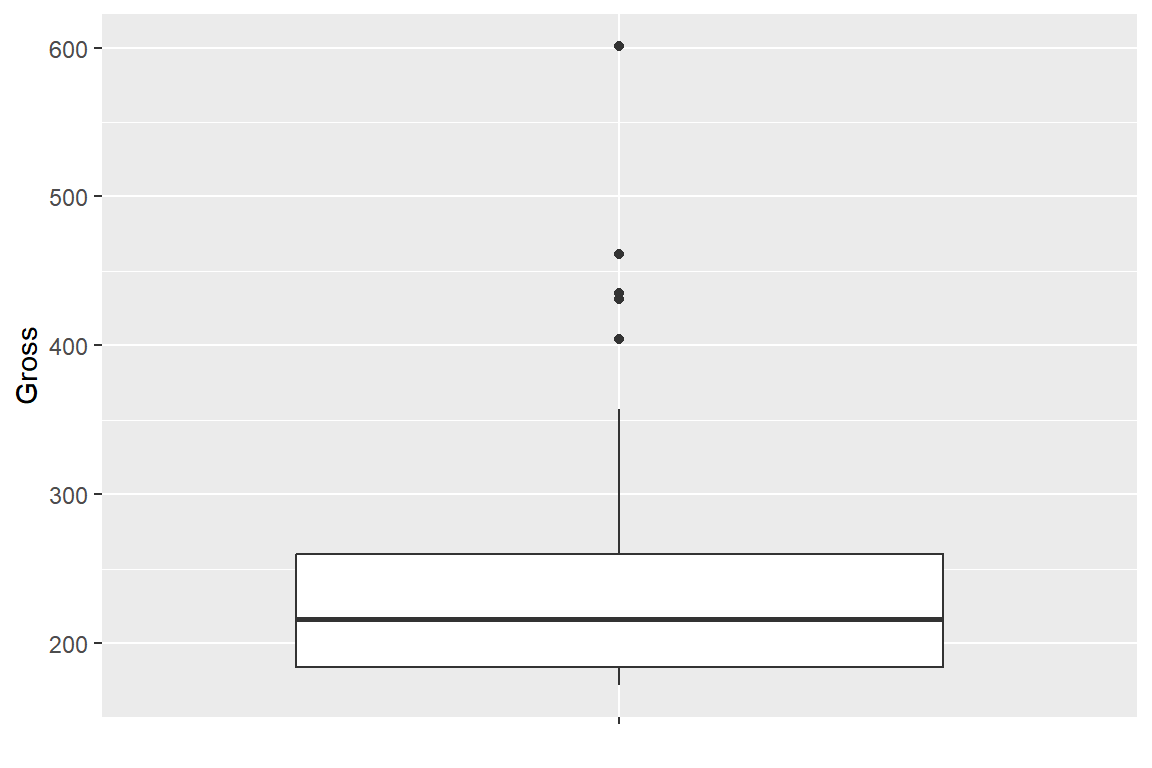
변수 `Gross`의 수직방향 상자그림

그림 9.23: 변수 Gross의 수직방향 상자그림 

library(tidyverse)
ggplot(alltime.movies, aes(y = "", x = Gross)) + 
  geom_boxplot() +
  ylab(NULL)
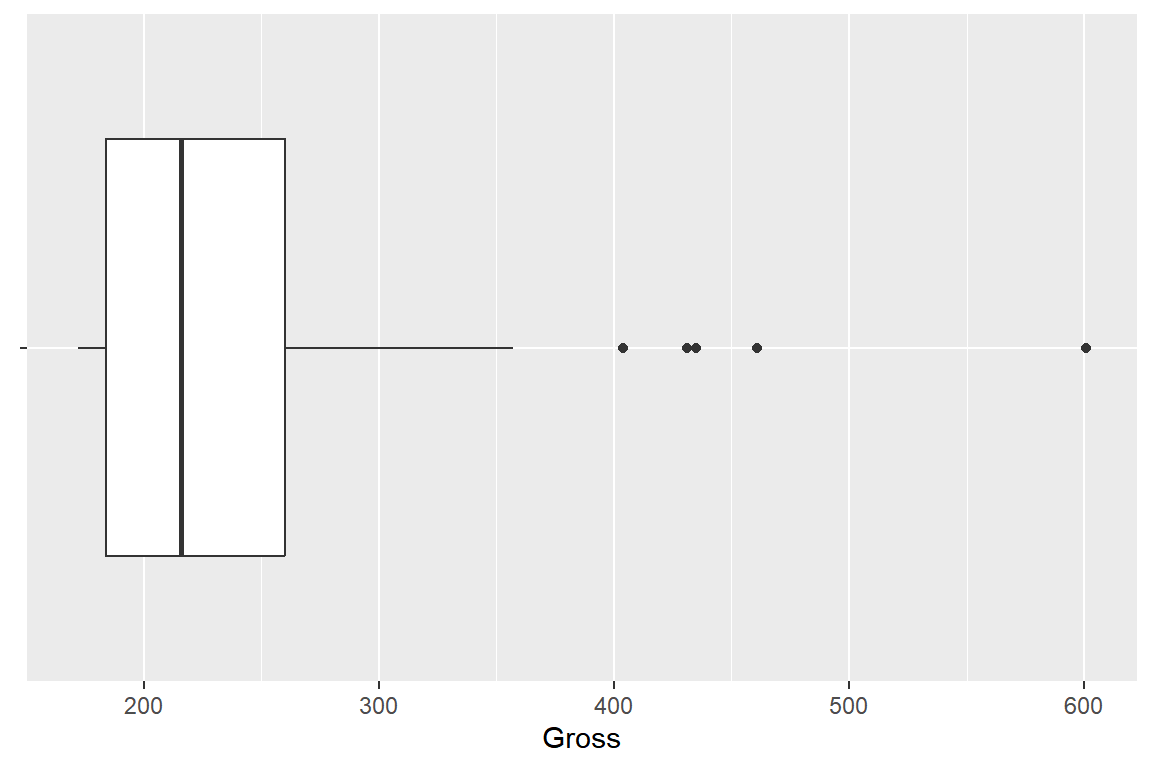
변수 `Gross`의 수평방향 상자그림

그림 9.24: 변수 Gross의 수평방향 상자그림

함수 geom_boxplot()으로 작성된 그림 9.24 의 상자그림에 표시된 이상값이 어떤 케이 스에 해당되는 것인지 확인해 보는 것은 중요한 작업이 될 수 있다. 이러한 작업에 필요한 함수는 ggplot_build()이다. 이 함수에 ggplot 객체를 입력하면 그래프 작성에 사용된 모든 내용을 보여준다. 생성된 결과는 리스트로서 각 레이어(layer) 작성에 필요한 통계량이 데이터 프레임 형태로 입력되어 있다. 이제 그림 9.24를 작성한 ggplot 객체를 함수 ggplot_build()에 입력하고 생성된 리스트의 첫 번째 요소인 데이터 프레임의 내용을 살펴보자.

bp <- ggplot(alltime.movies, aes(y = "", x = Gross)) + 
  geom_boxplot()
ggplot_build(bp)[[1]][[1]] |> 
  str()
## 'data.frame':    1 obs. of  26 variables:
##  $ xmin       : num 172
##  $ xlower     : num 184
##  $ xmiddle    : num 216
##  $ xupper     : num 260
##  $ xmax       : num 357
##  $ outliers   :List of 1
##   ..$ : num  601 461 435 431 404
##  $ notchupper : num 230
##  $ notchlower : num 202
##  $ y          : 'mapped_discrete' num 1
##  $ flipped_aes: logi TRUE
##  $ PANEL      : Factor w/ 1 level "1": 1
##  $ group      : int 1
##  $ xmin_final : num 172
##  $ xmax_final : num 601
##  $ ymin       : 'mapped_discrete' num 0.625
##  $ ymax       : 'mapped_discrete' num 1.38
##  $ xid        : num 1
##  $ newx       : num 1
##  $ new_width  : num 0.75
##  $ weight     : num 1
##  $ colour     : chr "grey20"
##  $ fill       : chr "white"
##  $ alpha      : logi NA
##  $ shape      : num 19
##  $ linetype   : chr "solid"
##  $ linewidth  : num 0.5

이상값으로 나타난 변수 Gross의 값은 $outliers에 리스트로 입력되어 있다. 이것을 벡터 형태로 추출해 보자.

bp_out <- ggplot_build(bp)[[1]][[1]]$outliers[[1]]
bp_out
## [1] 601 461 435 431 404

이제 변수 Gross가 위의 값을 갖는 관찰값들이 어떤 케이스, 즉 어떤 영화의 총수입에 해당되는지를 알아보자. 우선 영화제목이 데이터 프레임 alltime.movies의 rownames로 입력되어 있는데, 이것을 데이터 프레임에 변수로 포함시켜 보자.

alltime <- alltime.movies |>
  rownames_to_column(var = "Movie.Title") |>
  as_tibble() |> 
  print(n = 3)
## # A tibble: 79 × 3
##   Movie.Title                               Gross Release.Year
##   <chr>                                     <dbl>        <dbl>
## 1 "Titanic                                "   601         1997
## 2 "Star Wars                              "   461         1977
## 3 "E.T.                                   "   435         1982
## # ℹ 76 more rows

이제 데이터 프레임 alltime에서 변수 Gross의 값이 bp_out의 값과 같은 케이스를 패키지 dplyr의 함수 filter()에 연산자 %in%을 사용하여 선택해 보자.

alltime |>
  filter(Gross %in% bp_out)
## # A tibble: 5 × 3
##   Movie.Title                               Gross Release.Year
##   <chr>                                     <dbl>        <dbl>
## 1 "Titanic                                "   601         1997
## 2 "Star Wars                              "   461         1977
## 3 "E.T.                                   "   435         1982
## 4 "Star Wars: The Phantom Menace          "   431         1999
## 5 "Spider-Man                             "   404         2002

상자그림에 자료의 위치를 점으로 함께 나타내는 것도 나름 의미가 있는 그래프가 된다. 함수 geom_point()를 추가하면 되는데, 이때 한 가지 주의할 점은 함수 geom_boxplot()에서 이상값을 점으로 표시하지 않도록 해야 한다는 것이다. 이 작업은 옵션 outlier.shape = NA 또는 ourlier.color = NA 또는 outlier.size = -1을 함수 geom_boxplot()에 포함시키면 된다.

ggplot(alltime.movies, aes(x = "", y = Gross)) +
  geom_boxplot(outlier.shape = NA) +
  geom_point(color = "red") +
  xlab(NULL)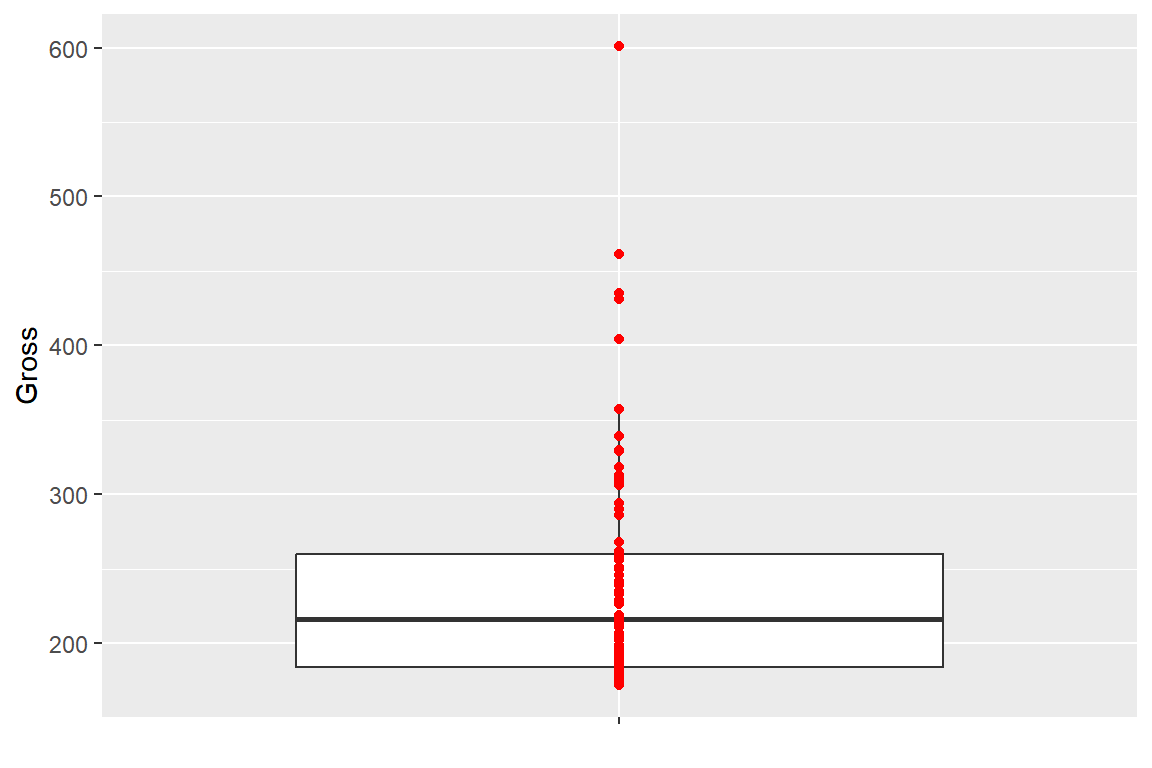
상자그림에 자료의 위치 추가

그림 9.25: 상자그림에 자료의 위치 추가

상자그림의 상자 안에 많은 점들이 서로 겹쳐져 있는 것을 볼 수 있다. 이런 경우에 점들의 위치에 약간 난수를 더해 조정해 주면 점들이 서로 겹쳐지는 문제를 어느 정도 해결 할 수 있는데, 함수 geom_jitter()로 할 수 있는 작업이다.

ggplot(alltime.movies, aes(x = "", y = Gross)) +
  geom_boxplot(outlier.shape = NA) +
  geom_jitter(color = "red", width = 0.01) +
  xlab(NULL)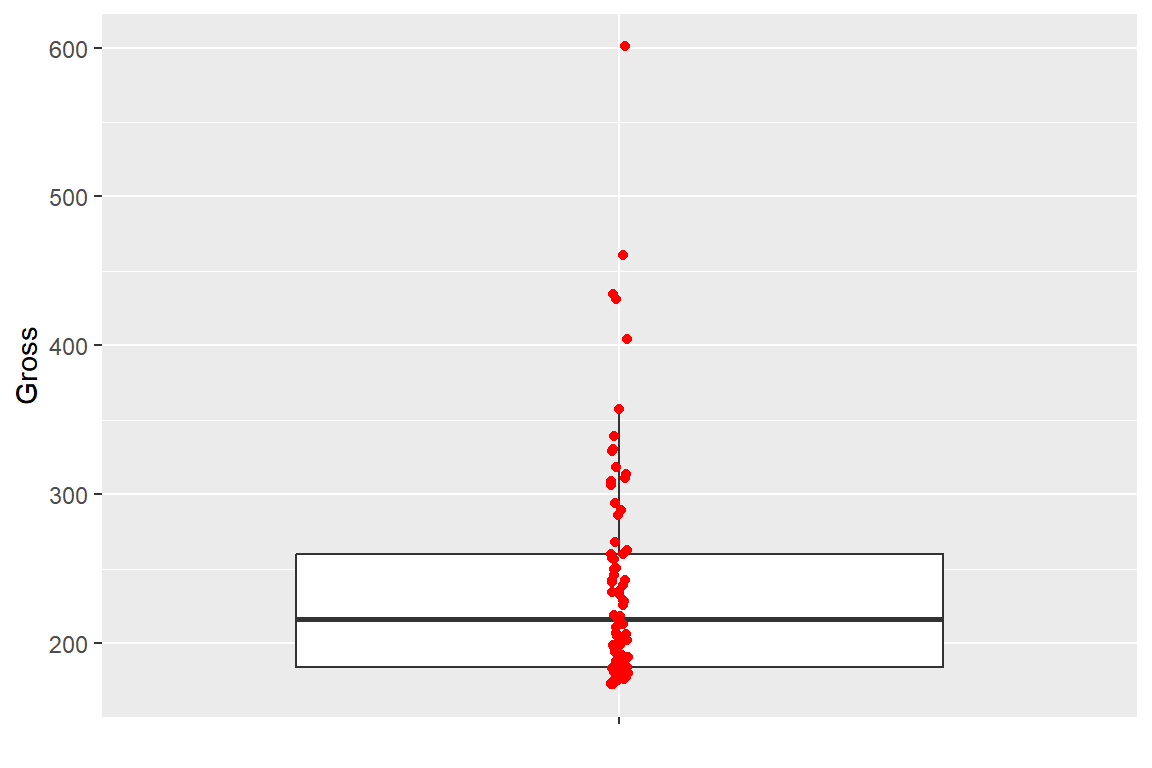
상자그림에 자료의 위치 추가

그림 9.26: 상자그림에 자료의 위치 추가

상자그림은 자료의 분위수를 기반으로 작성된 그래프이다. 따라서 중앙값의 위치는 표시가 되지만 평균값의 위치는 나타나지 않는 것이 일반적인 모습이다. 하지만 평균값의 위치를 추가적으로 표시하는 것이 자료의 분포를 이해하는 데 도움이 될 수도 있을 것이다.

자료의 요약통계량을 계산해서 그래프에 표시하는 작업은 함수 stat_summary()를 사용하면 할 수 있다. 이 함수는 개별 x값에 대하여 주어진 y값의 요약통계량 또는 개별 y값에 대하여 주어진 x값의 요약통계량을 계산하는 기능이 있다. 원하는 요약통계량은 변수 fun에 지정하고, 원하는 그래프 형태를 변수 geom에 지정하면 된다.

평균값이 빨간 십자 형태로 상자그림에 표시되었음을 알 수 있다.

ggplot(alltime.movies, aes(x = "", y = Gross)) + 
  geom_boxplot() +
  stat_summary(fun = "mean", geom = "point",
               color = "red", shape = 3, size = 4, stroke = 2) +
  xlab(NULL)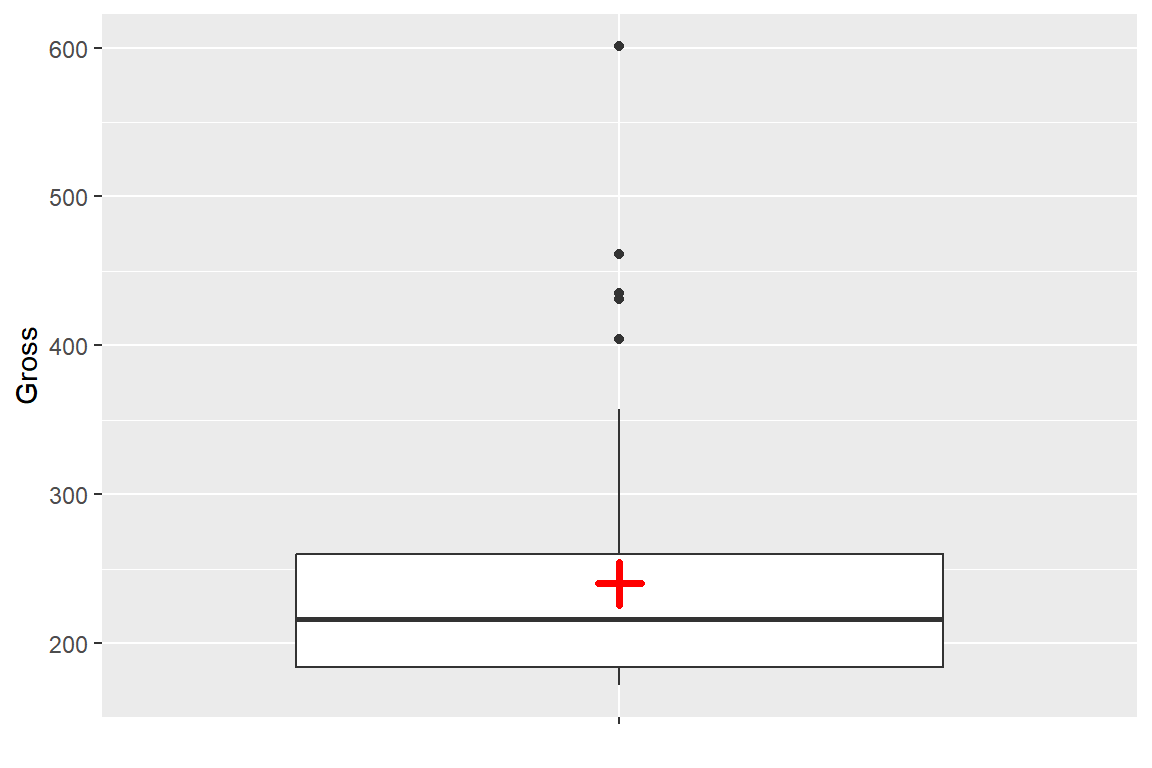
상자그림에 평균값 표시 추가

그림 9.27: 상자그림에 평균값 표시 추가

\(\bullet\) Violin plot

상자그림에 부가적인 정보를 추가한 변형된 형태의 상자그림이라고 할 수 있는 그래프로 violin plot이 있다. 이 그래프는 상자그림과 확률밀도함수 그래프의 조합이라고 할 수 있는데, 확률밀도함수 그래프는 9.3.4절에서 찾아볼 수 있다. Violin plot의 작성은 패키지 vioplot의 함수 vioplot()으로 할 수 있다.

library(vioplot)
vioplot(alltime.movies$Gross, col = "pink", xlab = " ")
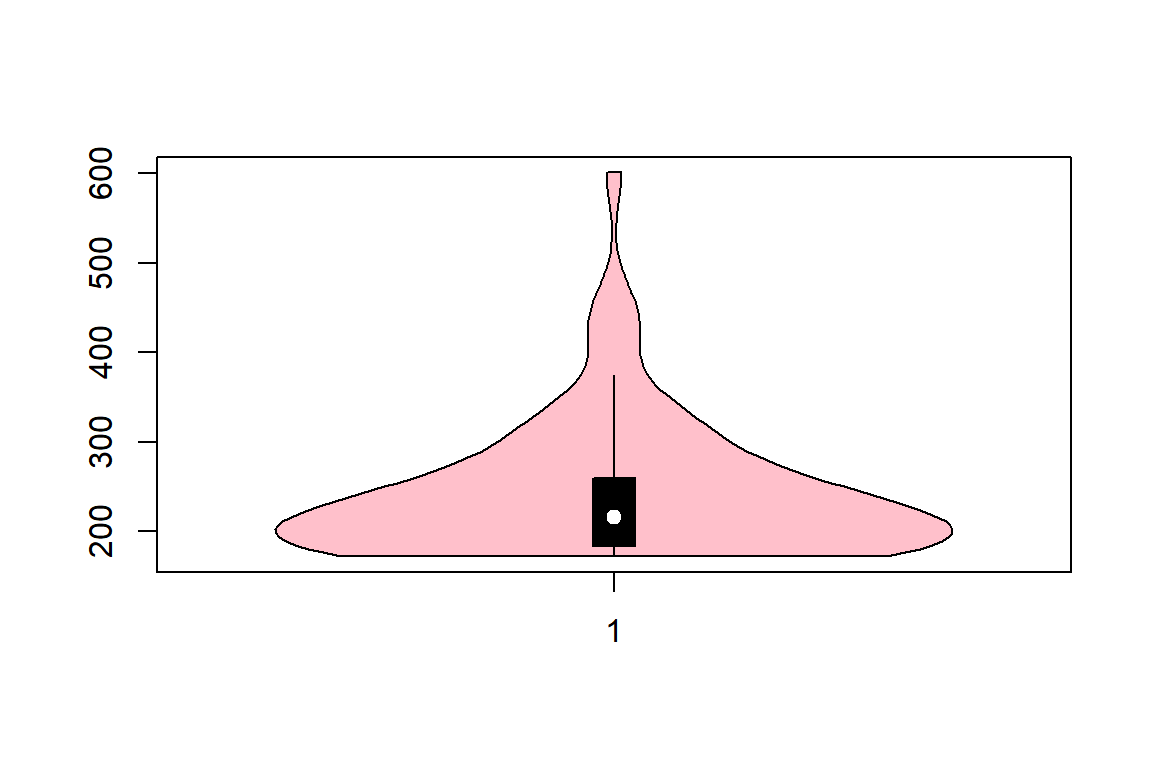
패키지 vioplot의 Violin plot: 수직방향

그림 9.28: 패키지 vioplot의 Violin plot: 수직방향 

vioplot(alltime.movies$Gross, col = "green", horizontal = TRUE)
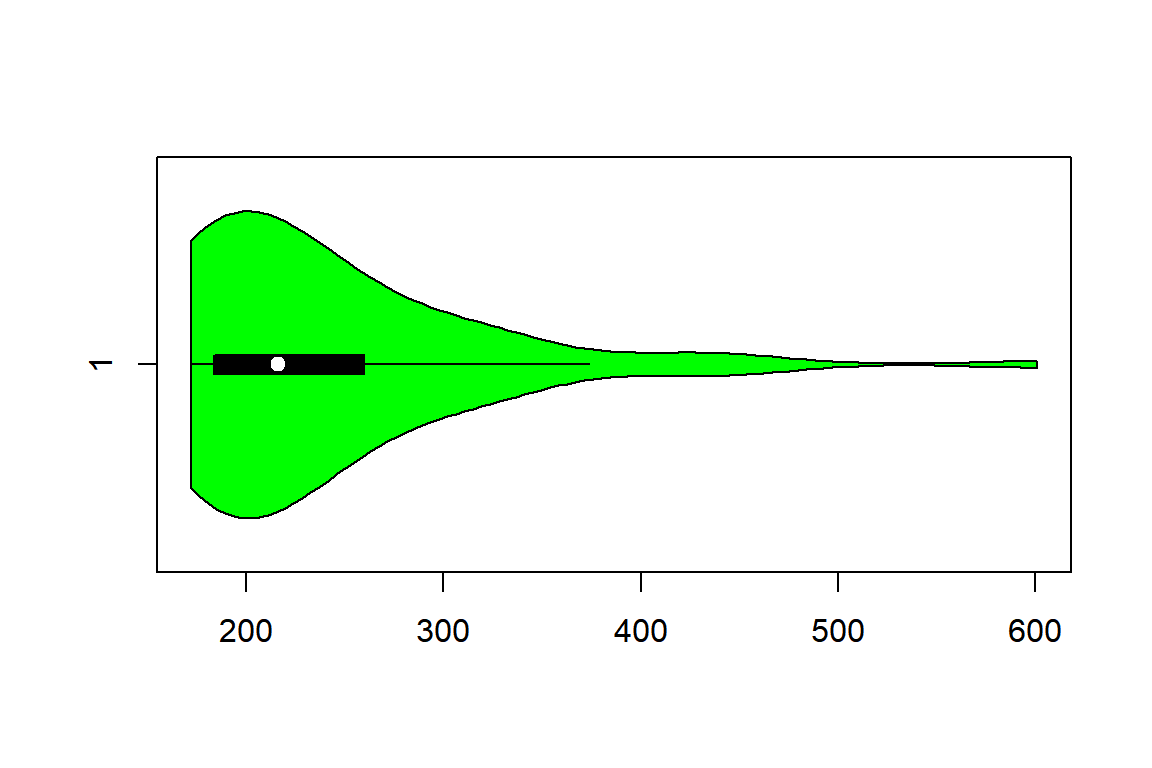
패키지 vioplot의 Violin plot: 수평방향

그림 9.29: 패키지 vioplot의 Violin plot: 수평방향

그림 9.28와 그림 9.29 에서 볼 수 있듯이 violin plot은 상자그림을 중심으로 확률밀도함수 그래프를 대칭으로 그려놓은 그래프이다. 하얀 점은 중앙값을 나타내고 있으며, 검은 상자는 0.25분위수에서 0.75분위수까지 그려져 있고, whisker는 검은색 실선으로 그려져 있다. 상자그림 외부의 그림은 확률밀도함수 그래프가 그려져 있어서 시각적으로 조금 더 분명하게 분포형태에 대한 정보를 제공해주고 있다. 많이 사용되고 있지는 않지만 상당히 효과적으로 사용할 수 있는 그래프라고 할 것이다.

패키지 ggplot2에서 violin plot의 작성은 함수 geom_violin()으로 할 수 있다. 이 함수는 상자그림없이 확률밀도함수 그래프만을 대칭으로 작성한다.

vio <- ggplot(alltime.movies, aes(x = "", y = Gross)) +
  xlab(NULL)
vio + geom_violin()
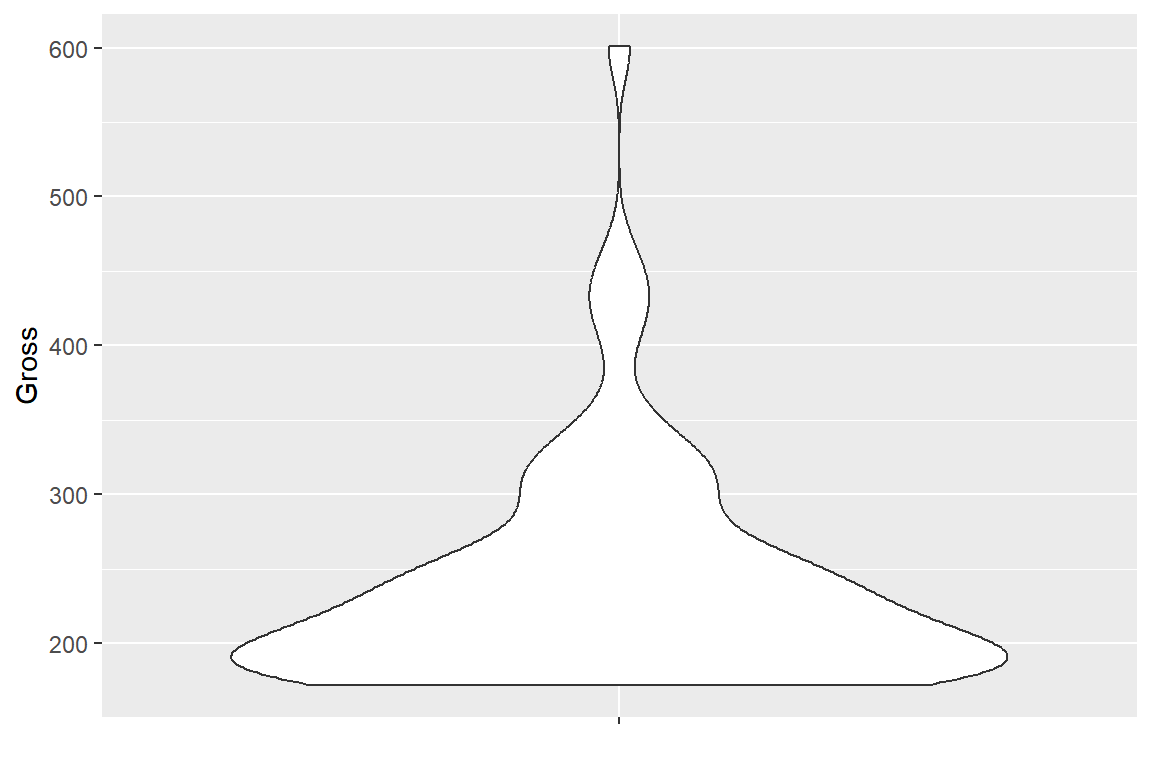
패키지 ggplot2의 violin plot

그림 9.30: 패키지 ggplot2의 violin plot

분위수를 함께 표시하고자 한다면 변수 draw_quantiles에 표시를 원하는 분위수를 지정해야 한다.

vio + geom_violin(draw_quantiles = c(0.25, 0.5, 0.75), fill = "lightblue")
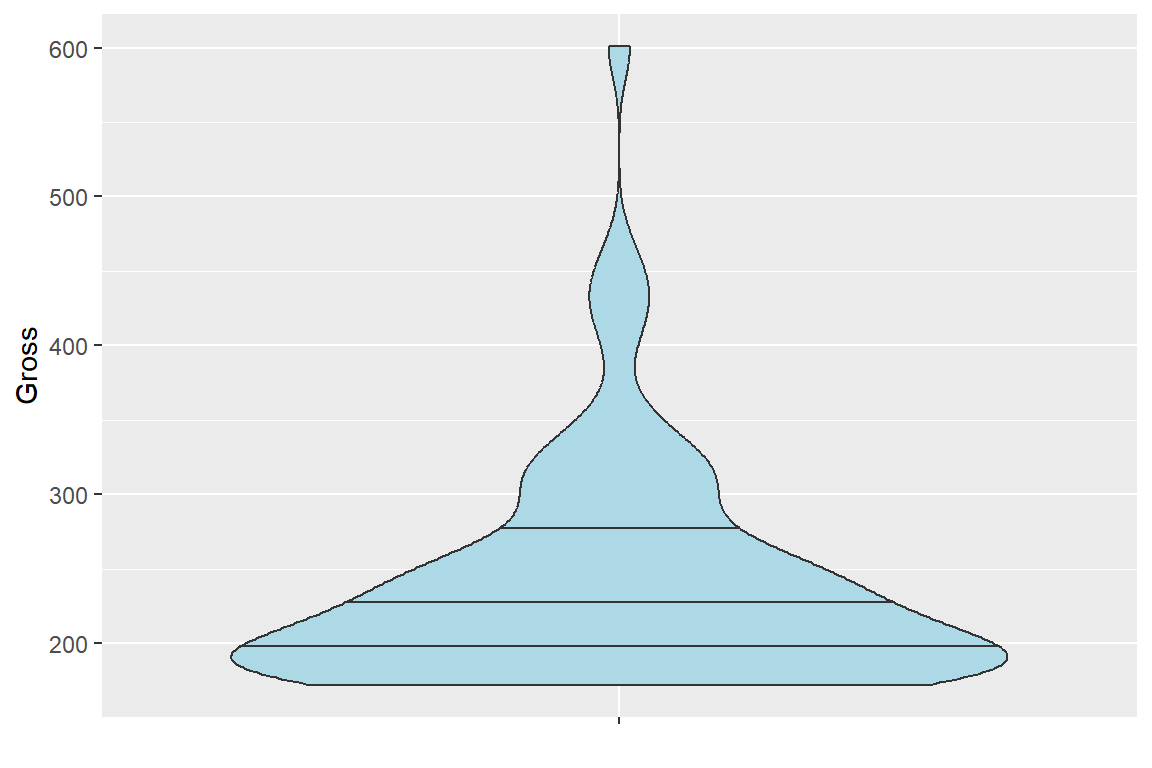
패키지 ggplot2의 violin plot: 분위수 함께 표시

그림 9.31: 패키지 ggplot2의 violin plot: 분위수 함께 표시

상자그림과 함께 violin plot을 작성하고자 한다면 함수 geom_boxplot()을 함께 사용하면 된다. 변수 width는 상자그림의 폭을 조절하기 위해 추가했다.

vio + geom_violin(fill = "lightblue") +
  geom_boxplot(width = 0.1)
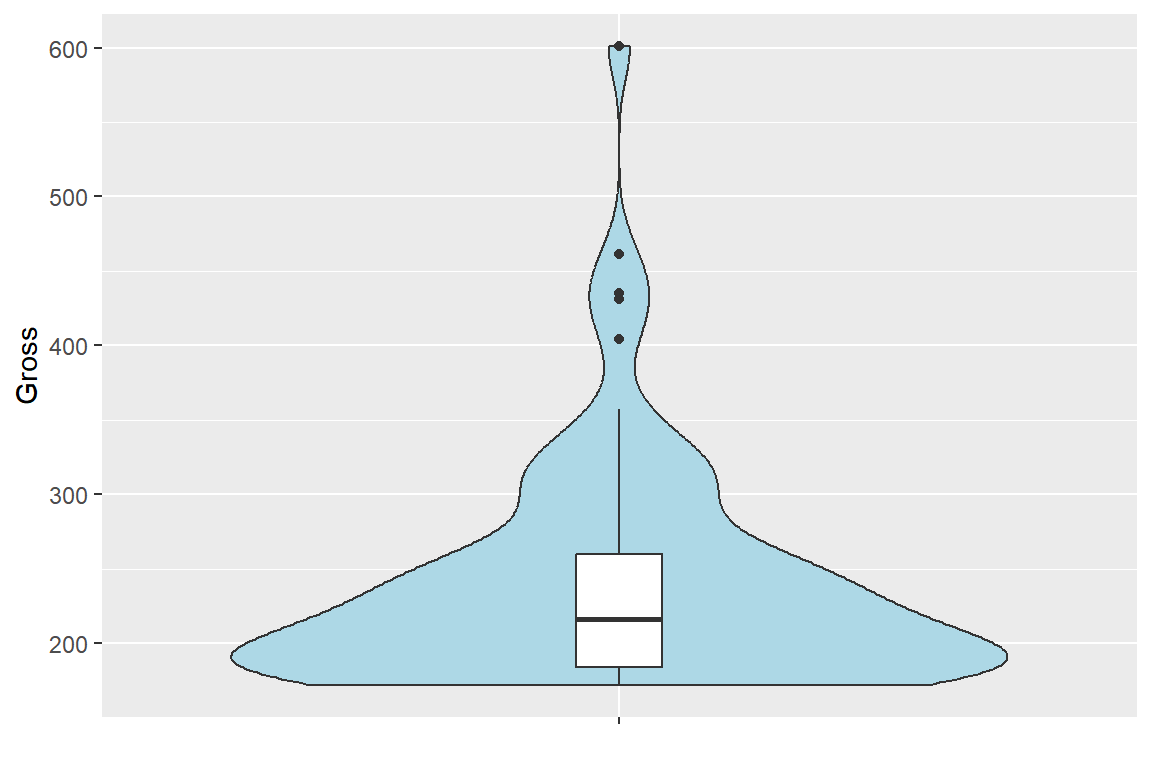
패키지 ggplot2의 violin plot: 상자그림 추가

그림 9.32: 패키지 ggplot2의 violin plot: 상자그림 추가

함수 geom_violin()을 함수 geom_boxplot()의 뒤에 추가한다면 투명도를 조절하는 시각적 요소인 alpha의 값을 낮게 지정하여 투명도를 높여야 상자그림이 보이게 된다.

vio + geom_boxplot(width = 0.1) +
  geom_violin(fill = "lightblue", alpha = 0.3)
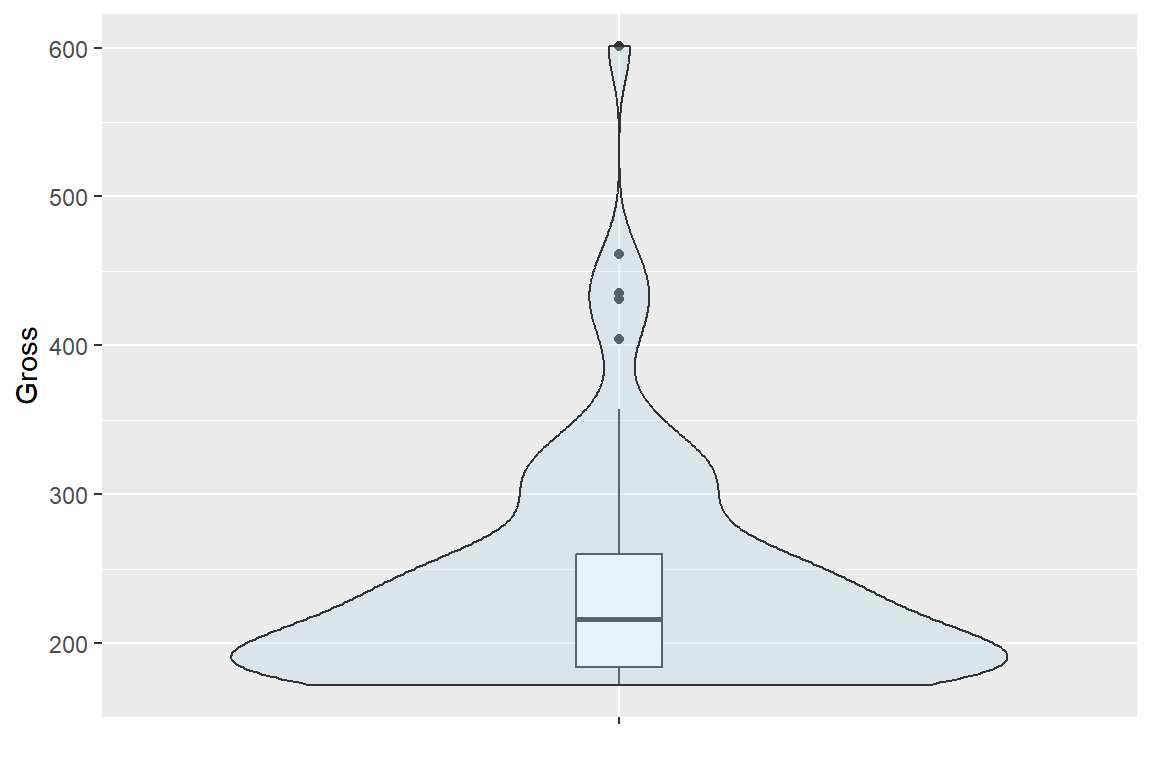
패키지 ggplot2의 violin plot: 상자그림 추가

그림 9.33: 패키지 ggplot2의 violin plot: 상자그림 추가

9.3.3 히스토그램

히스토그램은 연속형 자료의 분포를 시각화하는 데 가장 많이 사용되는 그래프 중 하나이다. 작성방법은 자료의 전 범위를 서로 겹치지 않는 구간(bin)으로 구분하고, 각 구간에 속한 자료의 빈도를 구한다. 이어서 각각의 구간을 X축으로, 그 구간에 대한 빈도수를 나타내는 값을 Y축으로 하여 막대를 그리면 된다.

패키지 ggplot2에서는 함수 geom_histogram()으로 히스토그램을 작성할 수 있다. 구간 설정은 구간의 개수를 bins에 지정하거나, 구간의 폭을 binwidth에 지정하면 된다. 디폴트는 bins = 30으로 히스토그램을 작성한다.

예제 데이터로 데이터 프레임 faithful을 사용해 보자. 이 데이터 프레임에는 미국 Yellowstone 국립공원에 있는 Old Faithful이라는 간헐천의 분출지속시간(eruptions)과 분출간격(waiting)이 변수로 있다. 이 중 분출간격에 대한 분포를 히스토그램으로 나타내보자. 히스토그램의 형태는 구간을 어떻게 설정하는가에 따라 크게 변하게 된다.

library(patchwork)
h1 <- ggplot(faithful, aes(waiting)) + geom_histogram() + ylab(NULL)
h2 <- ggplot(faithful, aes(waiting)) + geom_histogram(bins = 10) + ylab(NULL)
h3 <- ggplot(faithful, aes(waiting)) + geom_histogram(binwidth = 3) + ylab(NULL)
h1 + h2 + h3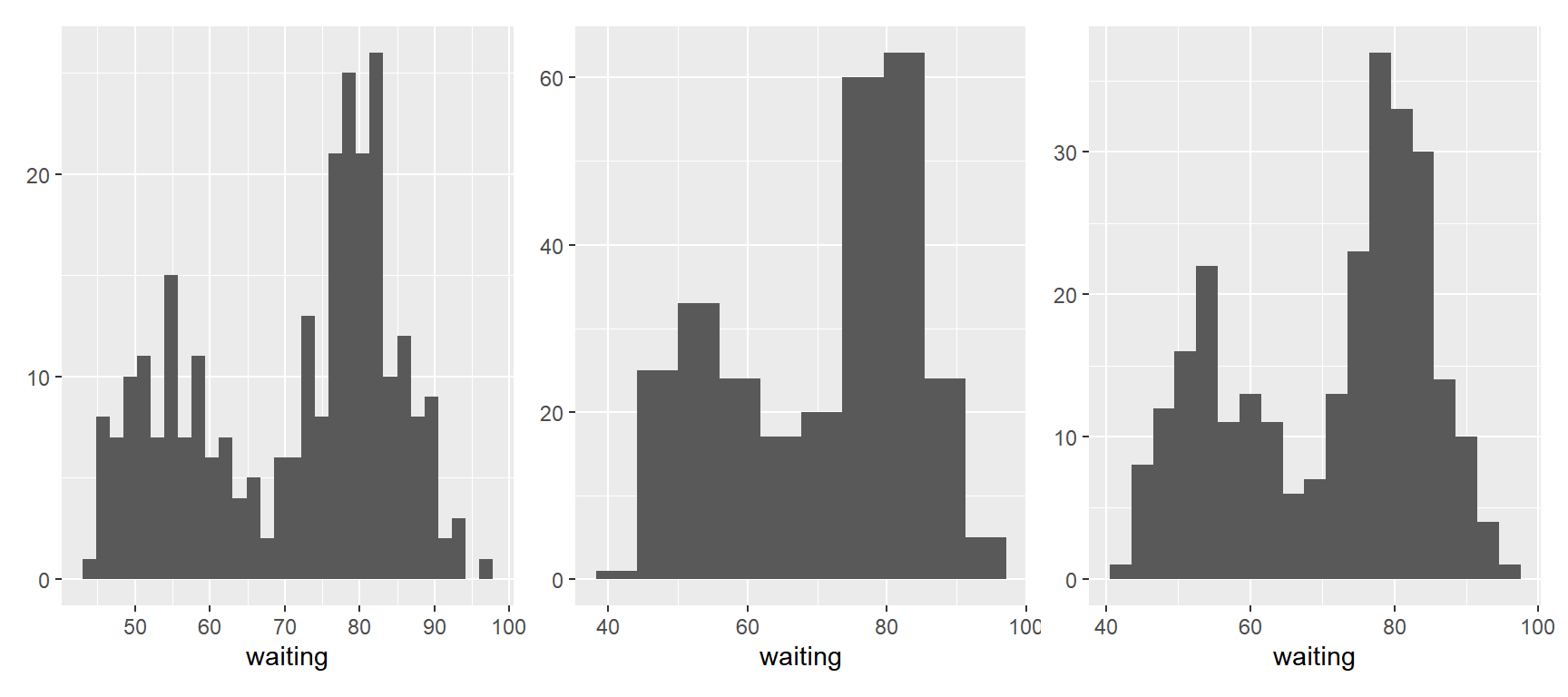
함수 `geom_histogram()`으로 작성한 히스토그램

그림 9.34: 함수 geom_histogram()으로 작성한 히스토그램

그림 9.34에서 볼 수 있듯이 구간을 어떻게 설정하는가에 따라 히스토그램의 모습이 크게 변하게 된다. 디폴트 구간으로 작성된 히스토그램이 만족스러운 결과를 보여주는 경우도 있겠지만 전적으로 의존하기에는 아쉬운 점이 많다. 이렇듯 구간설정 문제는 히스토그램의 중요한 문제라 할 수 있으나, 적절한 구간설정에 관한 이론적 접근에 대해서는 생략한다.

히스토그램의 또 한 가지 문제는 연속형 데이터의 분포를 계단 형태로 표현함으로써 생기는 어색함이라고 할 수 있다. 이것은 히스토그램의 태생적인 한계라고 할 수 있는데, 이 문제는 9.3.4절에서 살펴볼 확률밀도함수 그래프를 히스토그램에 겹쳐서 나타내거나, 도수분포다각형을 작성하는 것으로 어느 정도 완화할 수 있다.

9.3.4 확률밀도함수 그래프

연속형 자료의 분포형태를 알아보기 위한 그래프로써 지금까지 줄기-잎 그림, 상자그림, 히스토그램을 살펴보았다. 이 그래프들은 모두 나름의 장점이 있는 좋은 그래프들이다. 그러나 줄기-잎 그림은 대규모의 데이터에는 적합하지 않다는 단점이 있고, 상자그림은 사분위수를 기본으로 하여 나타낸 그래프이기 때문에 분포의 세밀한 특징이 잘 나타나지 않을 수 있다. 또한 연속형 자료의 분포는 매끄러운 곡선의 형태를 지니고 있으나 히스토그램은 항상 계단함수의 형태를 보일 수밖에 없다는 한계가 있다.

대규모의 데이터에도 쉽게 적용되며 분포의 세밀한 특징도 잘 나타내고, 또한 매끄러운 곡선으로 분포의 형태를 나타낼 수 있는 방법이 바로 확률밀도함수를 추정하여 그래프로 나타내는 것이다. 분포 형태를 매우 효과적으로 나타낼 수 있기 때문에 최근 많이 사용되고 있는 방법이다.

패키지 ggplot2에서는 함수 geom_density()로 확률밀도함수 그래프를 작성할 수 있다. 다만 이때 주의할 점은 그래프를 표시할 X축의 구간을 자료의 실제 구간보다 더 넓게 잡아주어야 한다는 것인데, 그렇지 않았을 경우에는 꼬리가 잘린 형태의 확률밀도함수가 추정되어 그래프로 작성된다. 또한 X축에 자료의 위치를 눈금으로 표시해 주는 Rug plot은 함수 geom_rug()를 추가하면 작성된다.

library(patchwork)
d1 <- ggplot(faithful, aes(waiting)) + geom_density(fill = "skyblue") + ylab(NULL)
d2 <- ggplot(faithful, aes(waiting)) + geom_density(fill = "skyblue") + ylab(NULL) + xlim(30, 110)
d3 <- ggplot(faithful, aes(waiting)) + geom_density(fill = "skyblue") + geom_rug() + ylab(NULL) + xlim(30, 110) 
d1 + d2 + d3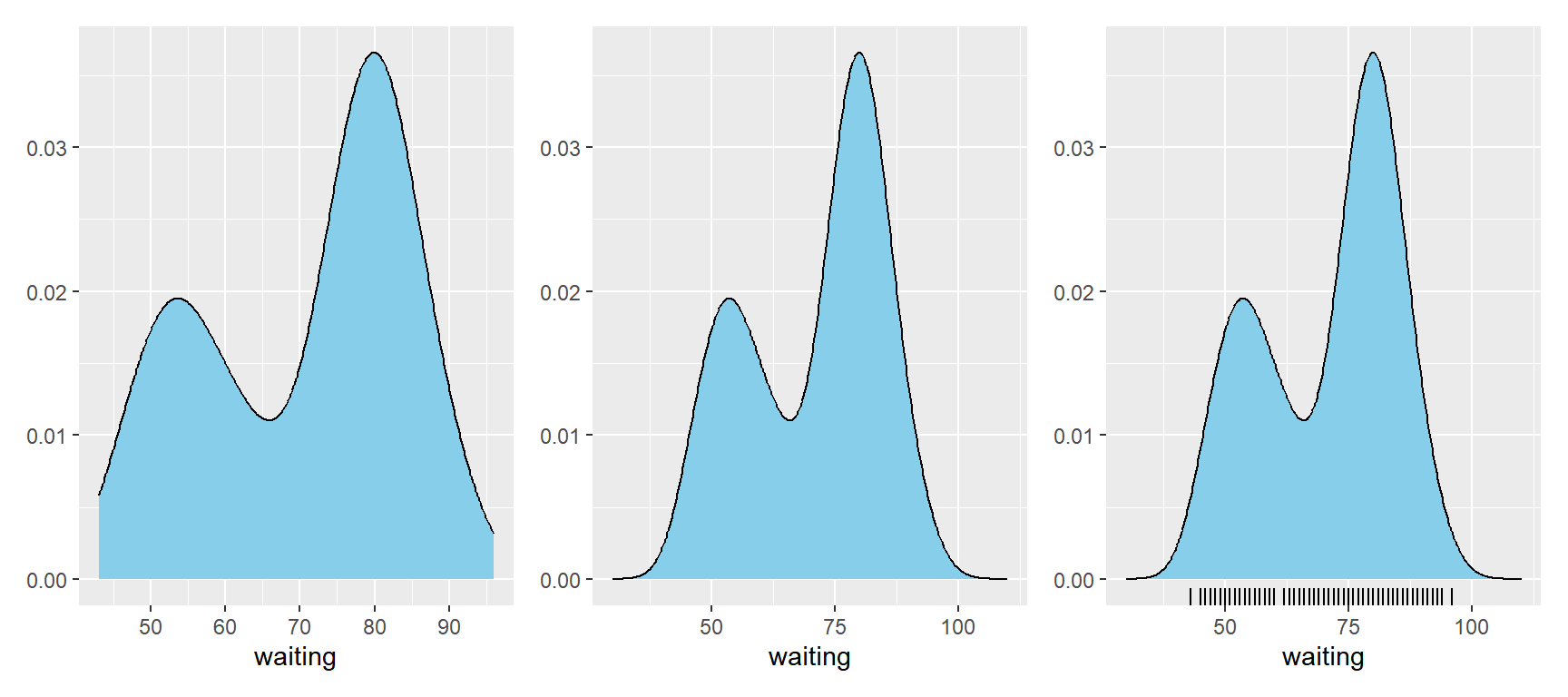
함수 `geom_density()`로 작성한 확률밀도함수 그래프

그림 9.35: 함수 geom_density()로 작성한 확률밀도함수 그래프

확률밀도함수 그래프는 단독으로 작성되는 경우도 많이 있지만, 히스토그램과 겹쳐서 작성하는 것도 의미 있는 작업이 된다. 히스토그램과 확률밀도함수 그래프를 겹치게 작성하기 위해서는 함수 geom_histogram()에서 시각적 요소 y에 변수 after_stat(density)를 매핑해야 히스토그램이 확률밀도로 표현된다. 이어서 함수 geom_density()로 확률밀도함수 그래프를 추가하면 된다.

ggplot(faithful, aes(x = waiting, y = after_stat(density))) +
  geom_histogram(fill = "red", binwidth = 5) +
  geom_density(color = "blue", linewidth = 1) +
  xlim(30, 110) + ylab(NULL)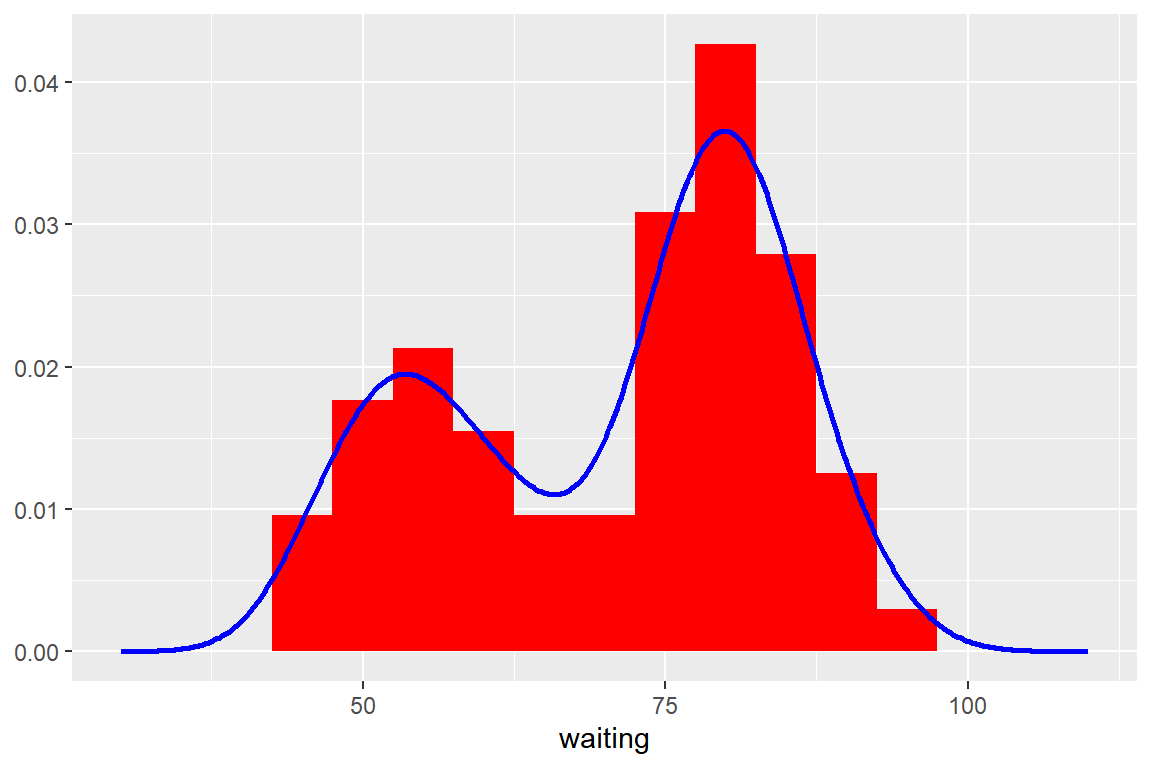
히스토그램과 확률밀도함수 그래프를 겹쳐지게 작성

그림 9.36: 히스토그램과 확률밀도함수 그래프를 겹쳐지게 작성

만일 geom_density()를 먼저 작성하고 geom_histogram()을 그 다음에 작성한다면 히스토그램을 투명하게 만드는 것이 필요하다.

ggplot(faithful, aes(x = waiting, y = after_stat(density))) +
  geom_density(color = "blue", linewidth = 1) +
  geom_histogram(fill = "red", binwidth = 5, alpha = 0.6) +
  xlim(30, 110) + ylab(NULL)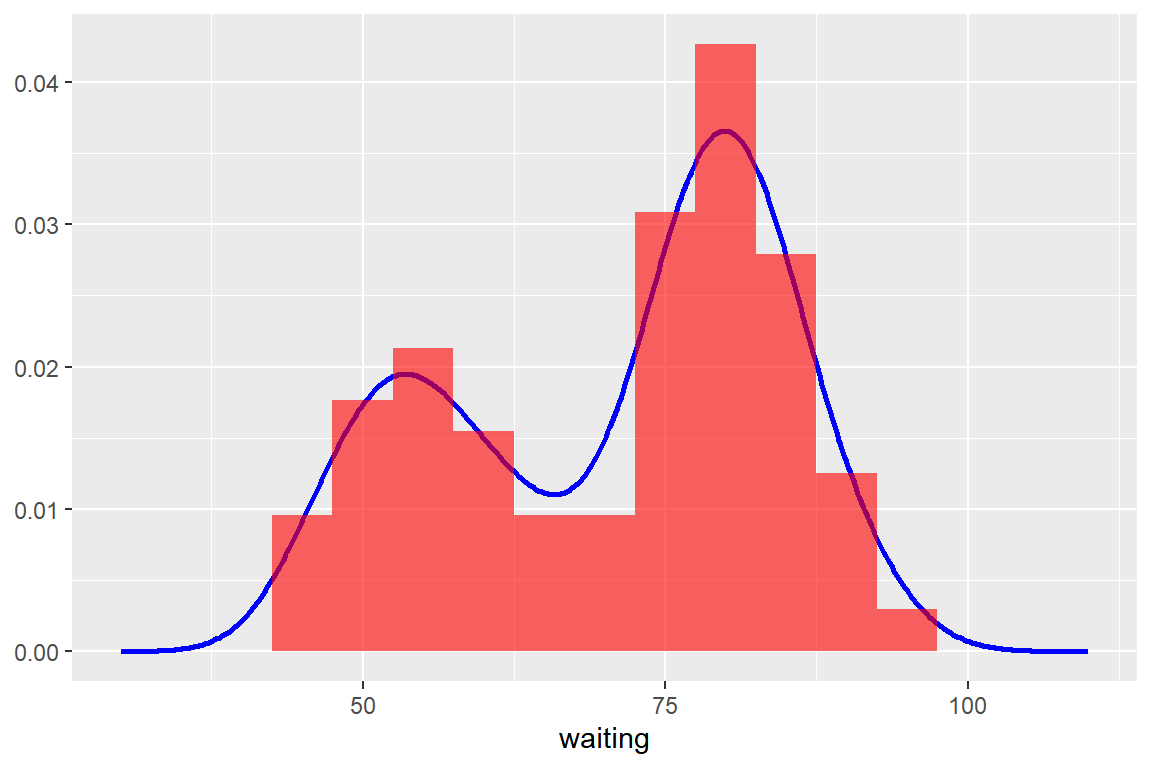
히스토그램과 확률밀도함수 그래프를 겹쳐지게 작성

그림 9.37: 히스토그램과 확률밀도함수 그래프를 겹쳐지게 작성

9.3.5 기타 유용한 그래프

지금까지 살펴본 그래프 외에 연속형 변수의 분포를 나타내는 유용한 그래프를 더 살펴보자.

\(\bullet\) 도수분포다각형(frequency polygon)

히스토그램이 각 구간에 속한 자료의 도수를 높이로 하는 막대로 분포를 나타내는 데 반하여 도수분포다각형은 각 구간의 도수를 선으로 연결한 다각형으로 분포를 나타내는 그래프이다. 그래프의 작성은 함수 geom_freqpoly()로 할 수 있으며, 사용법은 geom_histogram()과 동일하다.

예제로 데이터 프레임 faithful의 변수 waiting에 대한 도수분포다각형을 작성해 보자.

library(patchwork)
fp1 <- ggplot(faithful, aes(waiting)) + geom_freqpoly(binwidth = 5)
fp2 <- ggplot(faithful, aes(waiting, after_stat(density))) + geom_freqpoly(binwidth = 5)
fp1 + fp2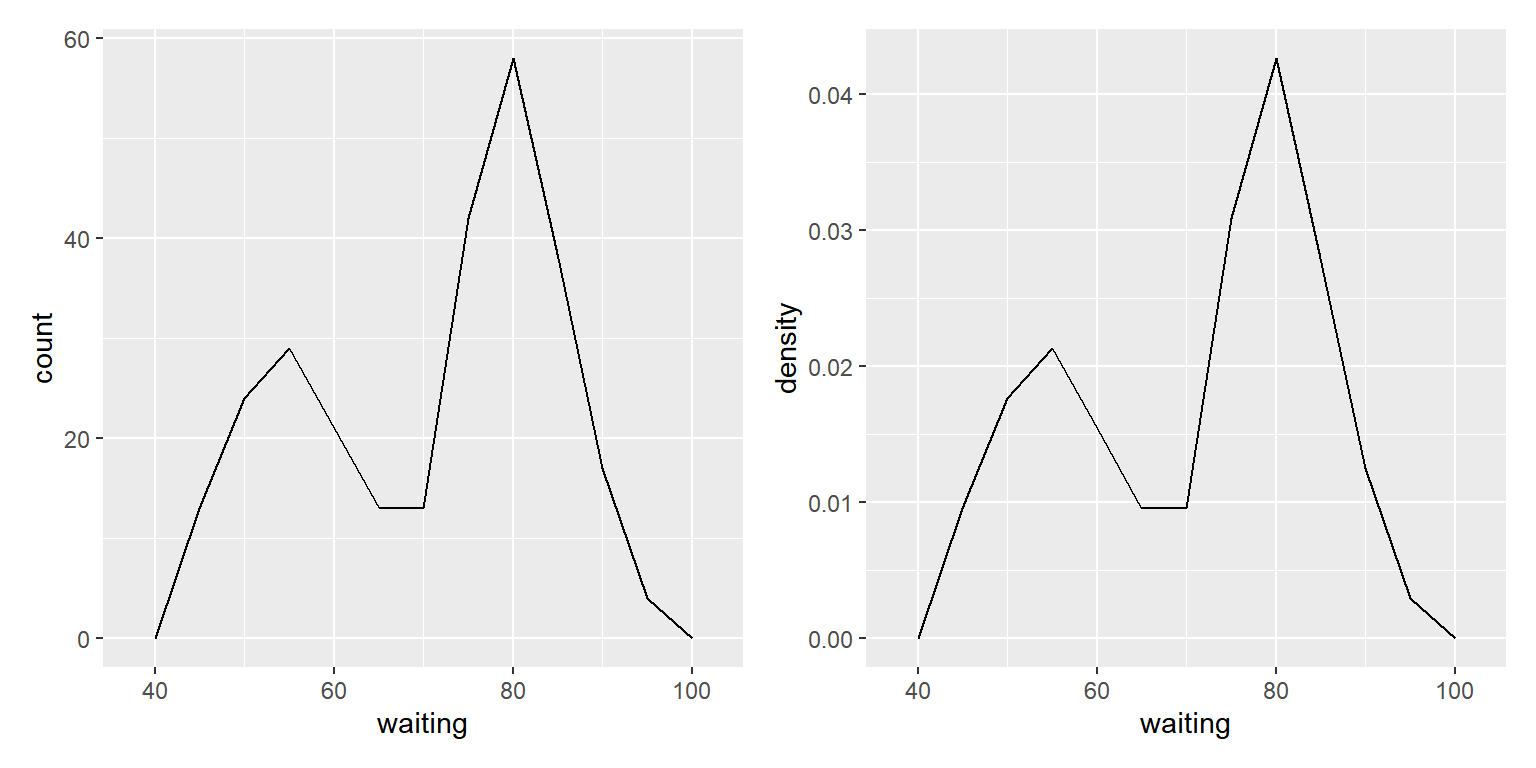
함수 `geom_freqpoly()`로 작성된 도수분포다각형

그림 9.38: 함수 geom_freqpoly()로 작성된 도수분포다각형

도수분포다각형은 범주형 변수에 의해 구분되는 그룹별로 연속형 변수의 분포를 비교하 는 경우에 히스토그램보다 더 유용하게 사용될 수 있는 그래프이다.

\(\bullet\) 점그래프(dot plot)

소규모 데이터의 분포를 표현할 때 유용하게 사용할 수 있는 그래프이다. 자료의 전 범위를 구간(bin)으로 구분하여 각 구간에 속한 자료 한 개당 하나의 점을 위로 쌓아 올리는 방식으로 작성되는 그래프이다. 패키지 ggplot2에서는 함수 geom_dotplot()으로 작성할 수 있으며, 구간의 간격은 변수 binwidth에 지정할 수 있다.

데이터 프레임 faithful의 변수 waiting에 대한 점그래프를 작성해 보자.

ggplot(faithful, aes(waiting)) + 
  geom_dotplot(binwidth = 1.5)
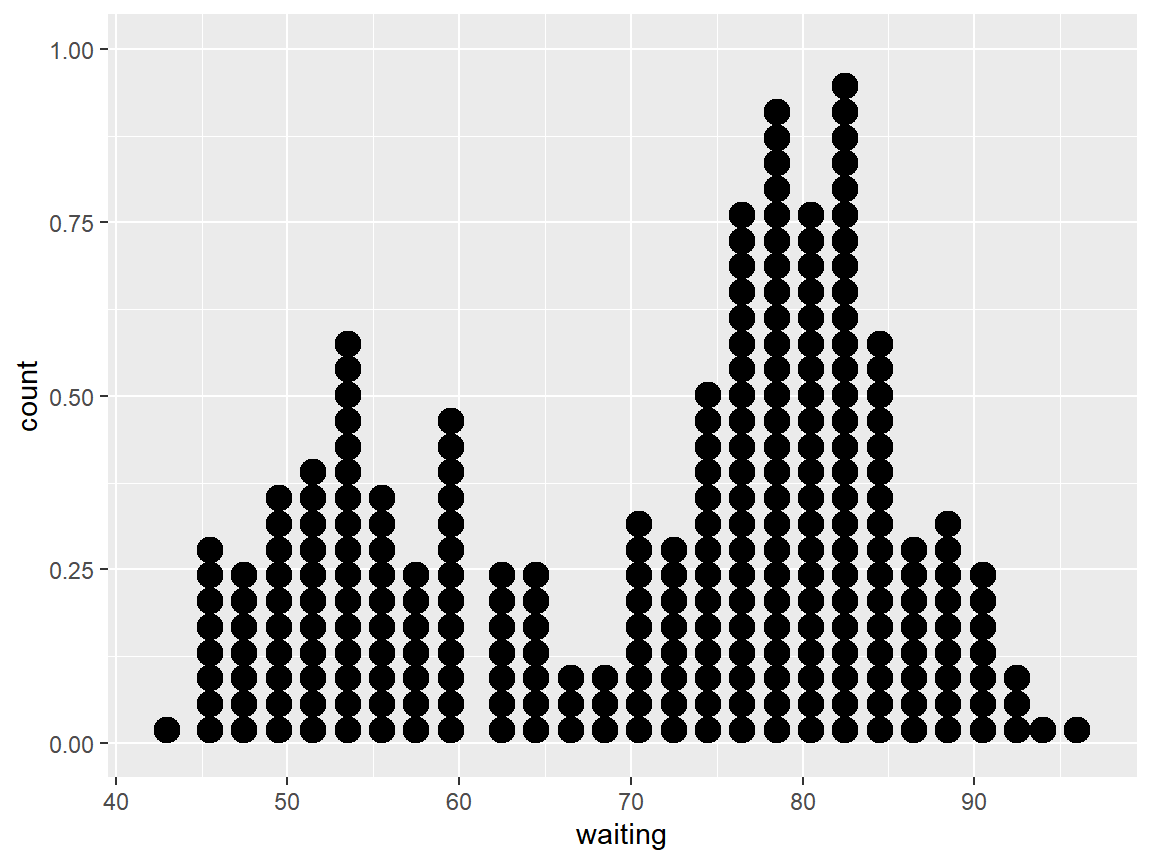
함수 `geom_dotplot()`으로 작성된 점 그래프

그림 9.39: 함수 geom_dotplot()으로 작성된 점 그래프

히스토그램과 유사한 특징을 보이는 그래프라는 것을 알 수 있다. 다만 그림 9.39의 Y축 scale이 잘못되어 있는데, 이것을 scale 함수로 제거하자.

ggplot(faithful, aes(waiting)) + 
  geom_dotplot(binwidth = 1.5) +
  scale_y_continuous(breaks = NULL)
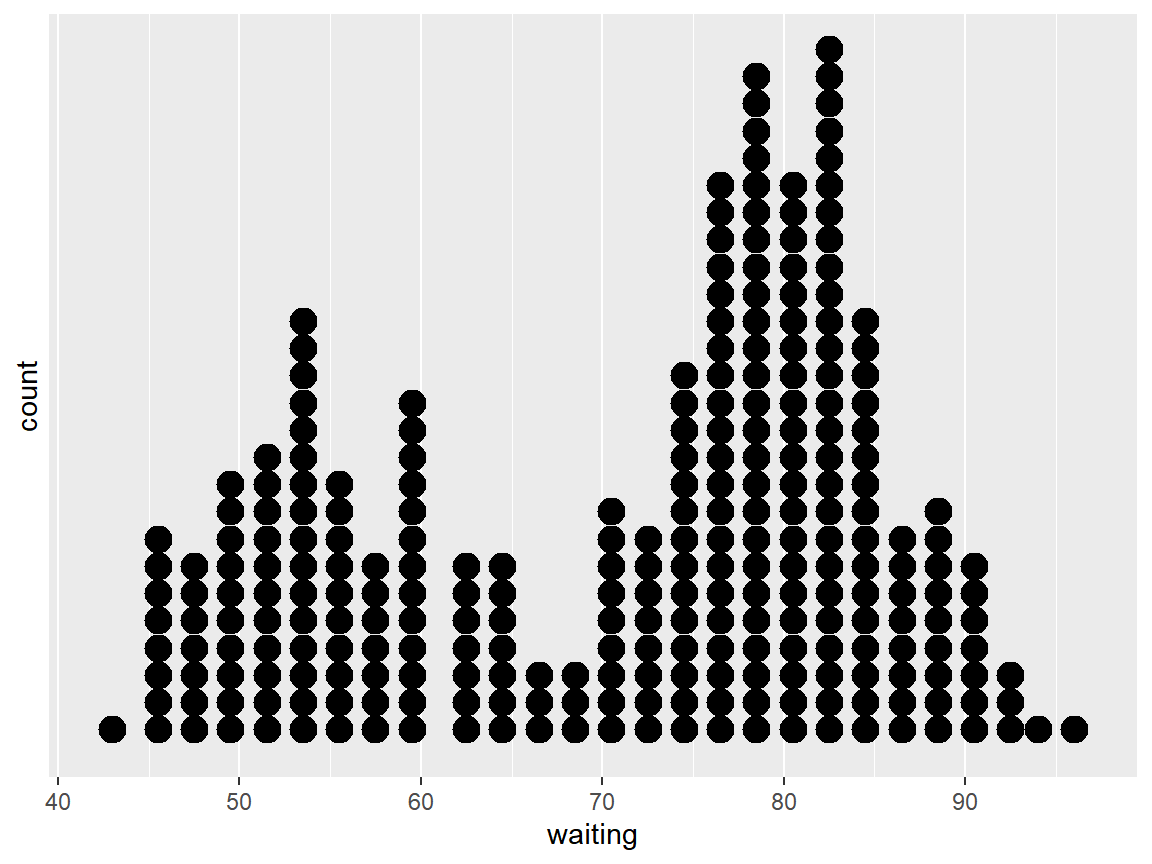
함수 `geom_dotplot()`으로 작성된 점 그래프

그림 9.40: 함수 geom_dotplot()으로 작성된 점 그래프

\(\bullet\) 경험적 누적분포함수 그래프

경험적 누적분포함수(empirical cumulative distribution function)는 각 자료값에서 \(1/n\) 의 높이를 갖고 증가하는 계단함수이다. 한 변수의 분포형태를 매우 정확하게 표현할 수 있는 그래프라고 할 수 있다. 다만 확률밀도함수가 아닌 분포함수를 나타내는 그래프이기 때문에 익숙하지 않은 사용자도 있을 것이다.

그래프의 작성은 stat_ecdf()로 할 수 있다. 데이터 프레임 faithful의 변수 waiting의 경험적 누적분포함수 그래프를 작성해 보자.

ggplot(faithful, aes(waiting)) +
  stat_ecdf()
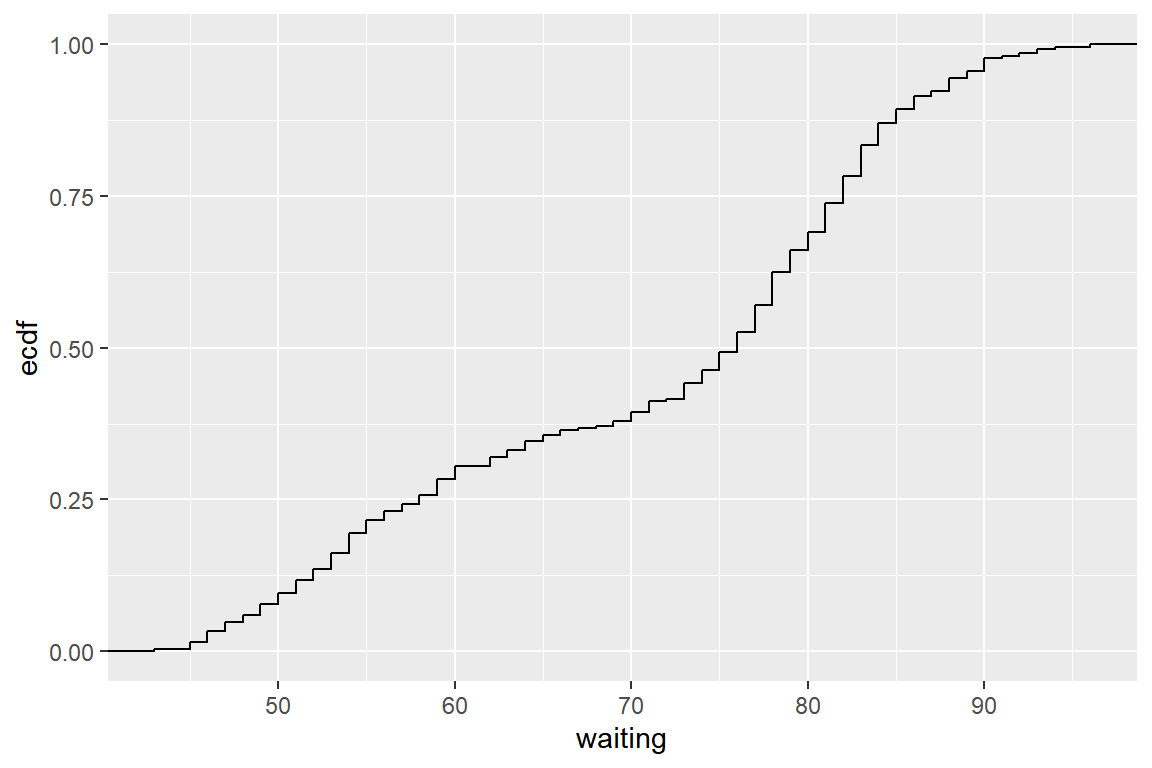
함수 `stat_ecdf()`로 작성된 경험적 누적분포함수 그래프

그림 9.41: 함수 stat_ecdf()로 작성된 경험적 누적분포함수 그래프

9.3.6 일변량 연속형 자료의 요약통계

일변량 자료분석의 첫 단계는 그래프를 이용하여 자료의 분포에 어떤 특징이 있는지를 살펴보는 것이다. 분포의 특징을 시각적으로 나타내는 것에 더하여 자료의 정보를 몇 개의 숫자로 요약해 주는 요약통계가 추가되면 다음 단계의 분석, 즉 다른 변수와의 비교 및 관계 탐구 등으로 나아가는 데 도움이 될 것이다. 이 절에서는 연속형 자료를 대상으로 자료의 중심을 나타내는 요약통계와 자료의 퍼짐을 나타내는 요약통계에 관련된 R 함수를 살펴보고자 한다.

\(\bullet\) 자료의 중심에 대한 요약통계

자료의 중심을 나타내는 요약통계량으로 가장 많이 사용되는 평균과 중앙값은 함수 mean()과 median()으로 각각 계산할 수 있다. 통계학개론에서 소개되는 최빈값은 연속형 데이터의 경우에는 의미가 없는 통계량이므로 여기에서는 다루지 않겠다.

자료에 결측값이 있는 경우, 함수 mean()과 median()의 계산 결과는 NA가 된다. 이런 경우에는 옵션 na.rm = TRUE를 포함시키면 자료에서 NA를 제외하고 나머지 자료만을 대상으로 계산을 하게 된다. 데이터 프레임 airquality의 변수 Ozone에는 다수의 결측값이 포함되어 있다. 변수 Ozone의 평균값과 중앙값을 각각 계산해보자.

my_stat <- list(m = ~ mean(.x, na.rm = TRUE),
                med = ~ median(.x, na.rm = TRUE))
airquality |> 
  summarise(across(Ozone, my_stat))
##   Ozone_m Ozone_med
## 1      42        32

분포의 형태가 좌우대칭에 가까운 경우에는 평균값이 가장 좋은 요약통계량이 되지만 좌측 또는 우측으로 심하게 치우친 분포의 경우에는 극단값에 큰 영향을 받지 않는 중앙값이 분포의 중심을 더 정확하게 나타내는 요약통계량이 될 것이다. 따라서 만일 평균값과 중앙값이 크게 차이가 난다면 치우친 형태의 분포가 될 가능성이 높은 것이다. 패키지 UsingR에 있는 데이터 프레임 cfb는 2001년 미국 소비자 재정상태에 관한 조사 데이터인데, 이 중 변수 INCOME에는 가구당 소득이 들어있다. 변수 INCOME의 분포형태를 살펴보자.

data(cfb, package = "UsingR")
cfb |> 
  summarise(across(INCOME, my_stat))
##   INCOME_m INCOME_med
## 1    63403      38033

평균값이 중앙값의 약 1.67배가 될 정도로 크게 차이가 나는 것을 볼 때 우측으로 심하게 치우친 분포, 즉 우측 꼬리가 매우 긴 분포임을 알 수 있다. 변수 INCOME의 정확한 분포의 형태를 알아보기 위하여 히스토그램을 작성해 보자.

ggplot(cfb, aes(x = INCOME, y = after_stat(density))) +
  geom_histogram(bins = 35, fill = "steelblue") +
  geom_density(color = "red", linewidth = 1)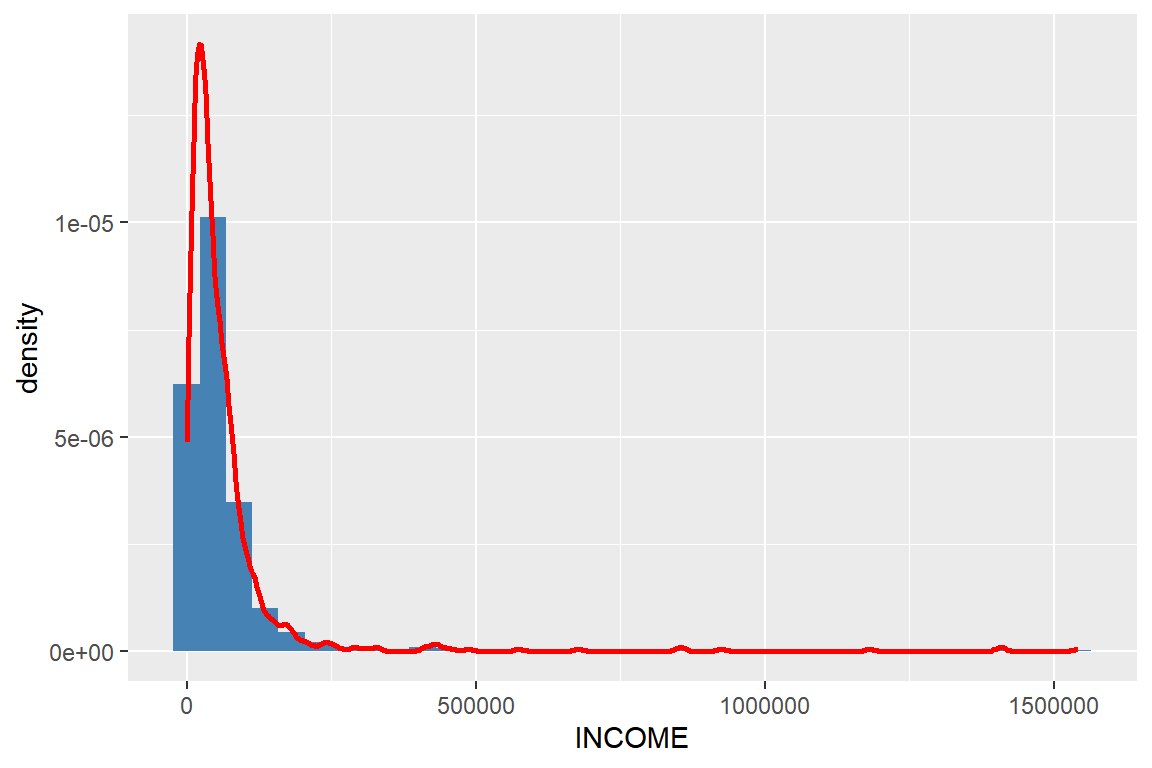
변수 `INCOME`의 히스토그램

그림 9.42: 변수 INCOME의 히스토그램

심하게 치우친 분포에 대해서는 대부분 변수변환을 통해 좌우대칭에 가까운 분포로 형태를 바꿔주게 된다. 변수 INCOME의 분포는 우측으로 심하게 치우친 분포이므로 로그 혹은 제곱근 변환을 통해 좌우대칭 분포로 변환시킬 수 있는데, 여기에서는 로그변환을 실시해보자.

cfb |> 
  mutate(log_income = log(INCOME)) |> 
  summarise(across(log_income, my_stat))
##   log_income_m log_income_med
## 1         -Inf             11

위 실행결과는 로그변환에서 주의할 점을 알려주고 있는데, 변수 log_income의 평균값이 -Inf가 된 것은 0이 포함된 변수 INCOME을 로그변환하였기 때문이다. 간단한 해결방안은 모든 자료를 우측으로 1만큼 이동시키는 것이다.

cfb |> 
  mutate(log_income = log(INCOME+1)) |> 
  summarise(across(log_income, my_stat))
##   log_income_m log_income_med
## 1     10.49809       10.54623

로그변환된 변수 INCOME의 분포를 히스토그램으로 나타내 보자.

cfb |> 
  mutate(log_income = log(INCOME+1)) |> 
  ggplot(aes(x = log_income, y = after_stat(density))) +
  geom_histogram(fill = "steelblue", bins = 35) +
  geom_density(color = "red", linewidth = 1)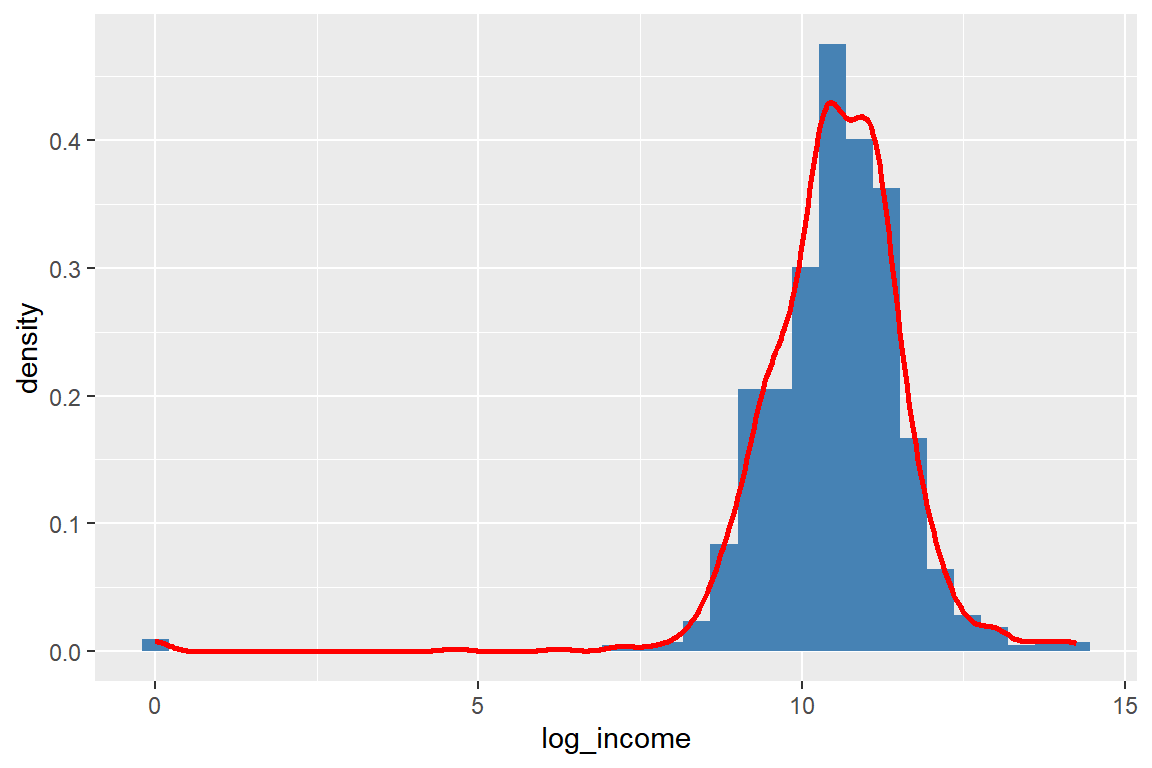
로그 변환된 변수 `INCOME`의 히스토그램

그림 9.43: 로그 변환된 변수 INCOME의 히스토그램

우측으로 심하게 치우친 모습을 보인 분포가 로그변환으로 좌우대칭의 모습을 보이는 분포로 바뀐 것을 알 수 있다. 그림 9.43의 좌측 끝부분에 있는 극단값은 변수 INCOME의 값이 0인 4개의 케이스에 해당되는 것이다.

\(\bullet\) 자료의 퍼짐정도에 대한 요약통계

자료의 중심에 대한 요약통계만으로는 자료의 분포에 대한 정확한 묘사가 불가능하다고 할 수 있는데, 다음에 주어진 시험점수 모의 자료를 살펴보자.

1차 시험(test1) 2차 시험(test2)
점수 75, 77, 80, 82, 85, 87, 88 50, 57, 80, 82, 86, 100, 100
평균 82 79.3

두 시험의 평균은 비슷하지만 자료의 퍼짐 정도에는 큰 차이가 있음을 알 수 있다. 자료의 퍼짐 정도를 측정하는 통계량에는 범위(range), 사분위범위(interquartile range), 표준편차 및 분산 등이 있다.

우선 1차 시험과 2차 시험 데이터의 범위를 구해 보자. 범위는 가장 단순한 자료 퍼짐 정도의 측정도구이다. 많은 수의 자료 중 오직 두 값(최솟값, 최댓값)만으로 계산하는 것이므로 전체 자료의 성격을 올바로 담아낼 수는 없다. 자료의 범위는 최솟값과 최댓값을 계산해주는 함수 range()의 결과를 함수 diff()에 입력하여 두 값의 차이를 계산하면 된다.

test1 <- c(75, 77, 80, 82, 85, 87, 88)
test2 <- c(50, 57, 80, 82, 86, 100, 100)
test1 |> range() |> diff()
## [1] 13
test2 |> range() |> diff()
## [1] 50

다음으로 사분위범위와 관련된 함수에 대해서 살펴보자. 사분위범위는 분위수 혹은 백분위수를 기반으로 정의되는 것이므로 분위수에 대해서 먼저 살펴보자. \(p\) 분위수란 전체 자료 중 \(100\times p \%\)의 자료보다는 크고 나머지 \(100 \times (1-p) \%\) 의 자료보다는 작은 수를 의미한다. 단, 여기서 \(p\) 의 범위는 \(0 \leq p \leq 1\) 이다. 백분위수는 분위수를 백분율로 표시한 것이다. 따라서 중앙값은 0.5분위수 및 50백분위수가 된다. 이어서 4분위수란 전체 데이터를 크기순으로 나열했을 때 4등분하는 3개의 수를 의미하는 것으로써 0.25분위수(\(Q_{1}\)), 중앙값, 0.75분위수(\(Q_{3}\))를 의미한다. 이제 사분위범위를 정의할 수 있는데, 사분위범위란 0.75분위수와 0.25분위수의 차이를 의미한다.

분위수의 계산은 함수 quantile()로 하며, 기본적인 사용법은 quantile(x, probs = seq(0, 1, by = 0.25), ...)이다. 함수 quantile()의 옵션 probs에는 원하는 확률값을 지정할 수 있으며, 생략되면 최솟값(0%), 최댓값(100%)을 포함한 4분위수가 출력된다. 이제 시험점수 모의 데이터에 함수 quantile()을 적용해 보자.

quantile(test1)
##   0%  25%  50%  75% 100% 
## 75.0 78.5 82.0 86.0 88.0
quantile(test2)
##    0%   25%   50%   75%  100% 
##  50.0  68.5  82.0  93.0 100.0
quantile(test1, probs = 0.25)
##  25% 
## 78.5
quantile(test2, probs = 0.25)
##  25% 
## 68.5

사분위범위는 함수 IQR()로 계산할 수 있다.

IQR(test1)
## [1] 7.5
IQR(test2)
## [1] 24.5

자료의 퍼짐 정도를 측정하는 도구로 가장 많이 사용되는 통계량이 표준편차와 분산이다. 두 통계량은 각 자료들이 자료의 평균에서부터 떨어진 거리를 이용하여 퍼짐 정도를 측정하고 있다. 대략적으로 표준편차는 각 관찰값들이 평균에서부터 떨어져 있는 거리의 평균값이라고 해석할 수 있다. 표준편차와 분산은 함수 sd()와 var()로 계산할 수 있다.

var(test1)
## [1] 24.66667
var(test2)
## [1] 377.5714
sd(test1)
## [1] 4.966555
sd(test2)
## [1] 19.4312

지금까지 살펴본 함수들과 함께 어울리며 일변량 자료의 요약통계를 계산하는 데 효과적으로 사용되는 함수가 summary()이다. 이 함수도 generic 함수로서 입력되는 객체의 class에 따라 다른 분석결과가 출력되는데, 숫자형 자료가 입력되면 4분위수와 평균값, 최솟값과 최댓값이 계산된다.

data(cfb, package = "UsingR")
summary(cfb$INCOME)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##       0   20558   38033   63403   69898 1541866

변수 INCOME의 평균값이 0.75분위수와 무척 가까운 값임을 알 수 있는데, 실제 평균값이 몇 분위수에 해당되는지 어떻게 계산할 수 있겠는가? 이것은 변수 INCOME의 각 관찰값들 중 평균값보다 작은 값들의 비율을 계산하면 되는데, 다음과 같이 간단하게 계산할 수있다. 변수 INCOME의 평균값이 0.705분위수에 해당한다는 것을 알 수 있다.

with(cfb, mean(INCOME <= mean(INCOME)))
## [1] 0.705

중심과 퍼짐 정도가 다른 자료들은 표준화 과정을 통하여 동일한 중심과 퍼짐 정도를 갖게 된다. 자료의 표준화는 함수 scale()로 할 수 있으며, 일반적인 사용법은 scale(x, center = TRUE, scale = TRUE)가 된다. x는 숫자형 행렬 또는 벡터가 되는데, 행렬인 경우에는 각 열 단위로 표준화가 진행된다. 시험점수 자료를 행렬로 묶어서 표준화를 실시해 보자.

cbind(test1, test2) |> scale()
##           test1       test2
## [1,] -1.4094277 -1.50714924
## [2,] -1.0067341 -1.14690381
## [3,] -0.4026936  0.03675974
## [4,]  0.0000000  0.13968700
## [5,]  0.6040404  0.34554153
## [6,]  1.0067341  1.06603239
## [7,]  1.2080809  1.06603239
## attr(,"scaled:center")
##    test1    test2 
## 82.00000 79.28571 
## attr(,"scaled:scale")
##     test1     test2 
##  4.966555 19.431197

시험점수자료의 변환 전 분포와 변환 후 분포를 나타낸 그래프가 그림 9.44에 있다.

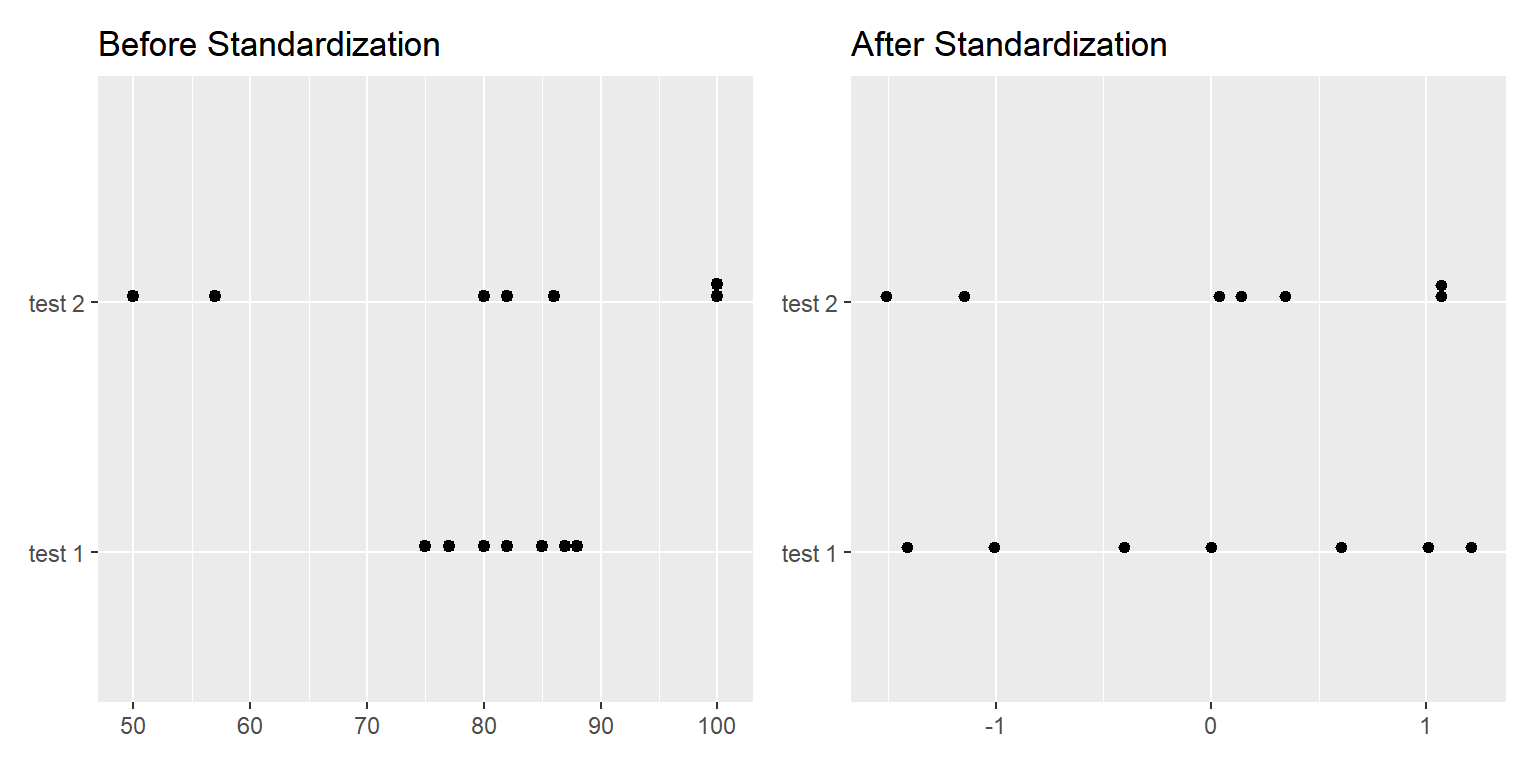
표준화 전후의 자료 분포

그림 9.44: 표준화 전후의 자료 분포

9.4 이변량 연속형 자료 탐색

연속형 변수가 두 개 혹은 그 이상 주어질 때 우리의 주된 관심은 변수들의 분포 비교와 변수 사이의 관계 탐색이라고 할 수 있다. 이 작업들은 그래프와 요약통계를 함께 이용해야 효과적으로 이루어질 수 있다.

9.4.1 연속형 변수의 분포를 비교하기 위한 그래프

두 개 이상의 연속형 변수의 자료가 주어졌을 경우, 그 변수들의 분포를 비교하는 것은 가장 기본적인 작업이라고 할 수 있다. 만일 어느 한 연속형 변수의 분포가 어떤 요인으로 구분되는 그룹마다 다르다면, 그것은 곧 그룹변수가 연속형 변수에 통계적으로 유의한 영향을 미치고 있다고 해석될 수 있다.

일변량 연속형 변수의 분포를 나타내는 그래프라면 분포의 비교 목적으로도 사용될 수 있을 것이다. 그룹별로 분포를 비교하고자 할 때 먼저 시도할 수 있는 것은 facet일 것이다. 함수 facet_wrap() 혹은 facet_grid()를 이용하여 그룹별로 분포를 나타내는 그래프를 작성해서 비교하는 것을 생각해 볼 수 있다. 다른 방법으로는 그룹별 그래프를 겹치게 작성하는 것이다. 하나의 그래프에서 비교하는 것이므로 의미있는 비교가 될 수 있을 것이다.

\(\bullet\) 히스토그램에 의한 그룹 자료의 분포 비교

예제로 패키지 ggplot2에 있는 데이터 프레임 mpg의 변수 cyl에 따른 연속형 변수 hwy의 분포를 비교해 보자. 변수 cyl은 자동차 엔진의 실린더 개수를 의미하는 것으로 4, 5, 6, 8의 네 가지 값을 갖는 숫자형 변수이고, 변수 hwy는 자동차의 고속도로 연비를 나타내는 변수이다. 먼저 변수 cyl로 구분되는 그룹에 속한 자료의 개수를 구해 보자.

library(tidyverse)
mpg |> count(cyl)
## # A tibble: 4 × 2
##     cyl     n
##   <int> <int>
## 1     4    81
## 2     5     4
## 3     6    79
## 4     8    70

변수 cyl이 5가 되는 자료의 개수가 너무 적다는 것을 알 수 있다. 따라서 변수 cyl이 4, 6, 8인 그룹에 대해서만 변수 hwy의 분포를 비교해 보자.

mpg_1 <- mpg |> 
  filter(cyl != 5)

먼저 facet 그래프를 작성해 보자. 그룹별 분포를 수월하게 비교할 수 있다.

ggplot(mpg_1, aes(hwy)) +
  geom_histogram(binwidth = 5) +
  facet_wrap(vars(cyl), ncol = 1)
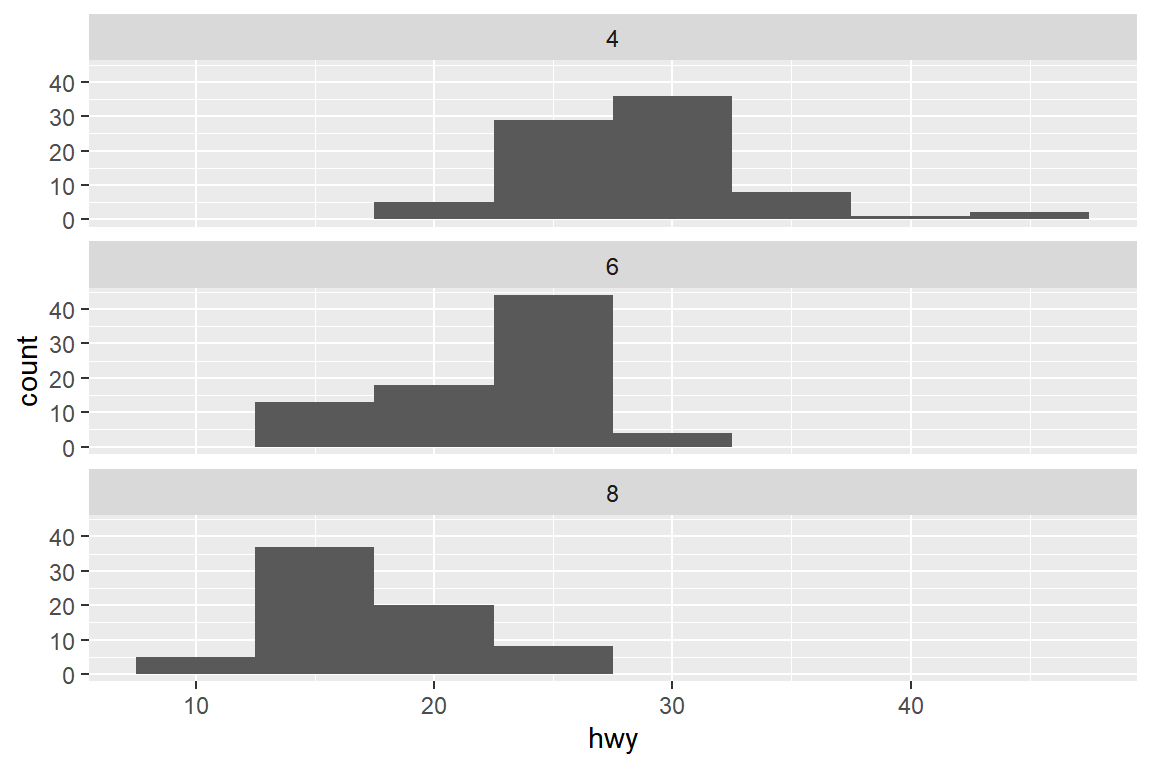
그룹 자료의 분포 비교를 위한 히스토그램

그림 9.45: 그룹 자료의 분포 비교를 위한 히스토그램

그룹별 히스토그램을 작성해서 하나의 그래프에 겹치게 나타내보자. 겹쳐진 히스토그램을 작성하기 위해서는 시각적 요소 fill에 요인을 매핑해야 한다. 또한 함수 geom_histogram()은 position = "stack"이 디폴트이기 때문에, 이 경우에는 position = "identity"로 변경해야 원하는 형태의 그래프를 작성할 수 있다. 히스토그램을 겹쳐 그리는 경우에는 투명도를 높이는 것이 분포 비교에 큰 도움이 되지 않음을 알 수 있다.

ggplot(mpg_1, aes(x = hwy, fill = factor(cyl))) +
  geom_histogram(binwidth = 5, alpha = 0.4, position = "identity") +
  labs(fill = "cyl")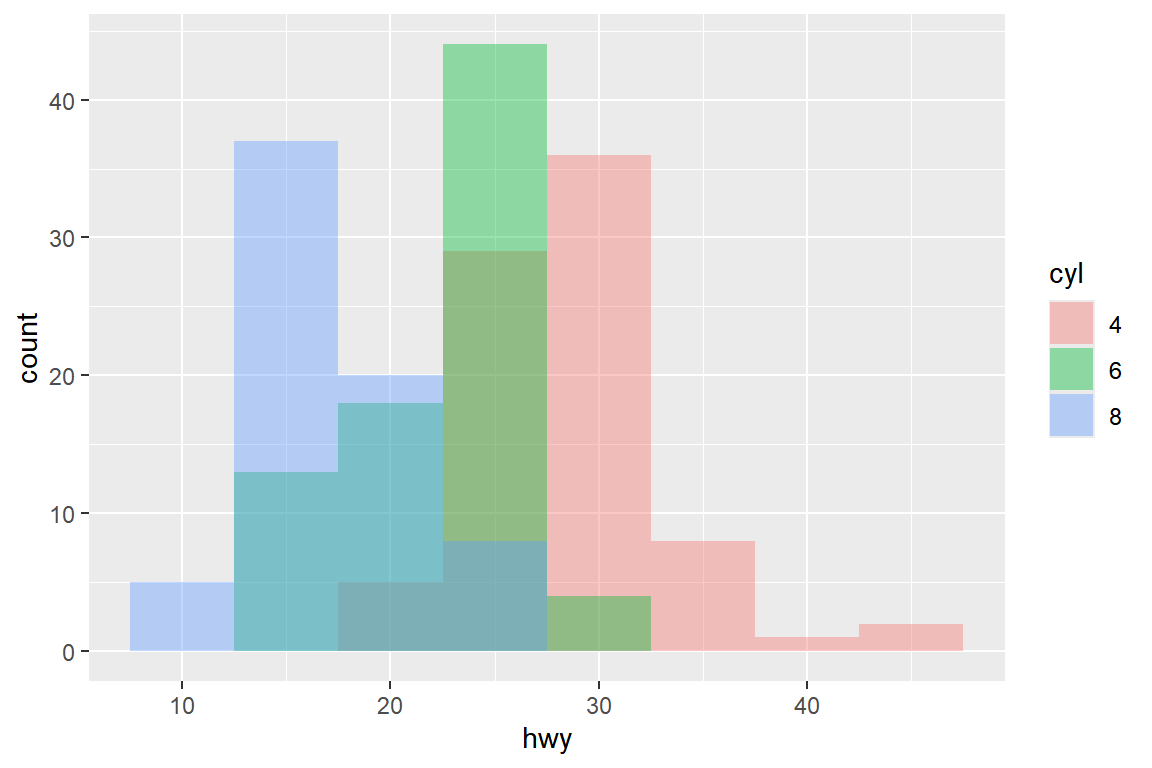
그룹 자료의 분포 비교를 위한 히스토그램

그림 9.46: 그룹 자료의 분포 비교를 위한 히스토그램

\(\bullet\) 도수분포다각형에 의한 그룹 자료의 분포 비교

패키지 ggplot2의 데이터 프레임 mpg의 변수 cyl에 따른 hwy의 분포를 비교해 보자. 변수 cyl이 5인 자료를 제외한 mpg_1을 사용하자.

함수 geom_freqpoly()에서 시각적 요소 color에는 요인을 매핑해야 겹쳐진 도수분포다각형이 작성된다. 각 그룹에 속한 자료의 개수가 다르게 때문에 빈도수에 의한 도수분포다각형으로는 그룹 간의 분포 비교가 부정확할 수 있다. 효과적인 비교를 하기 위해서는 상대도수를 사용하는 것이 더 바람직한 경우이다.

library(patchwork)
p1 <- ggplot(mpg_1, aes(x = hwy, color = factor(cyl))) +
  geom_freqpoly(binwidth=5, show.legend = FALSE, linewidth = 1)

p2 <- ggplot(mpg_1, aes(x = hwy, y = after_stat(density), color = factor(cyl))) +
  geom_freqpoly(binwidth=5, linewidth = 1) +
  labs(color = "cyl")

p1 +p2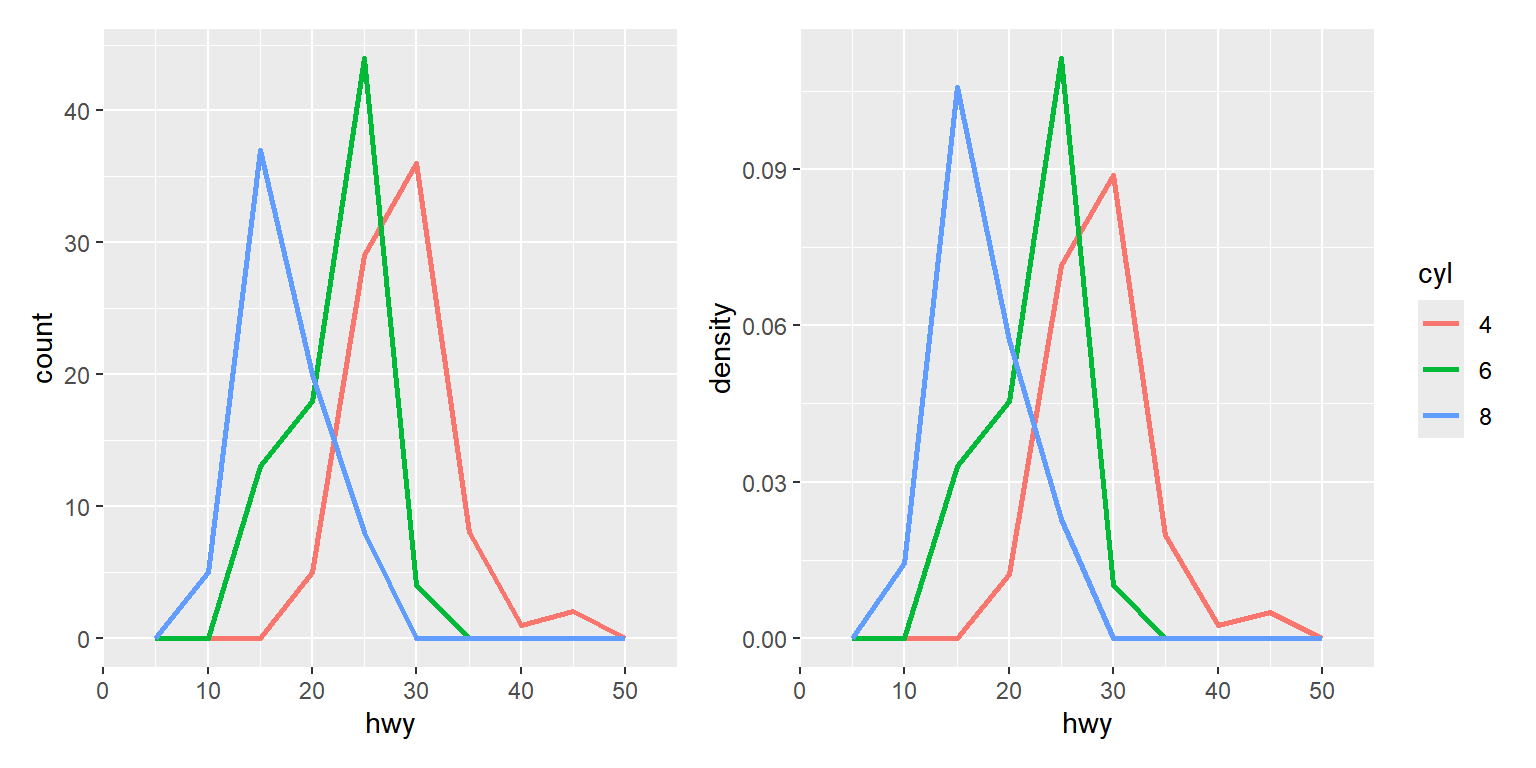
변수 `cyl`에 따른 `hwy`의 도수분포다각형

그림 9.47: 변수 cyl에 따른 hwy의 도수분포다각형

히스토그램과 도수분포다각형은 작성 과정에서 많은 부분을 공유하고 있는 그래프이며, 일변량 자료의 분포를 나타낼 때에는 모두 유용하게 사용되고 있다.

\(\bullet\) 나란히 서 있는 상자그림에 의한 그룹 자료의 분포 비교

상자그림의 경우에는 facet을 이용하는 것보다 그룹별로 작성된 상자그림을 옆으로 나란히 세워 놓는 것이 더 효과적으로 분포를 비교하는 방법이 될 것이다. 자료의 형태는 비교 대상이 되는 변수가 각기 독립된 벡터에 입력되어 있는 경우와 하나의 연속형 벡터와 그룹을 구분하는 하나의 요인으로 입력되어 있는 경우로 구분할 수 있다.

먼저 비교할 대상이 되는 변수들이 x1, x2, x3와 같이 개별적으로 구성된 경우를 살펴보자. 이런 경우 패키지 ggplot2에서는 자료를 데이터 프레임으로 구성하되, 개별적으로 구성된 벡터들을 하나의 연속형 벡터와 하나의 요인으로 나타내야 한다. 예제로 정규분포, t-분포, 균등분포에서 각각 발생시킨 난수의 분포를 나란히 서 있는 상자그림으로 비교해 보자.

set.seed(124)
x1 <- rnorm(100)
x2 <- rt(100, df = 3)
x3 <- runif(100, min = -1, max = 1)
tibble(x = c(rep(1:3, each = 100)), y = c(x1, x2, x3)) |>
  ggplot(aes(factor(x), y)) +
  geom_boxplot() +
  scale_x_discrete(labels = c("N(0,1)", "t(3)", "Unif(-1,1)")) +
  theme(axis.text.x = element_text(size = 15, face = "bold")) +
  labs(x = NULL, y = NULL)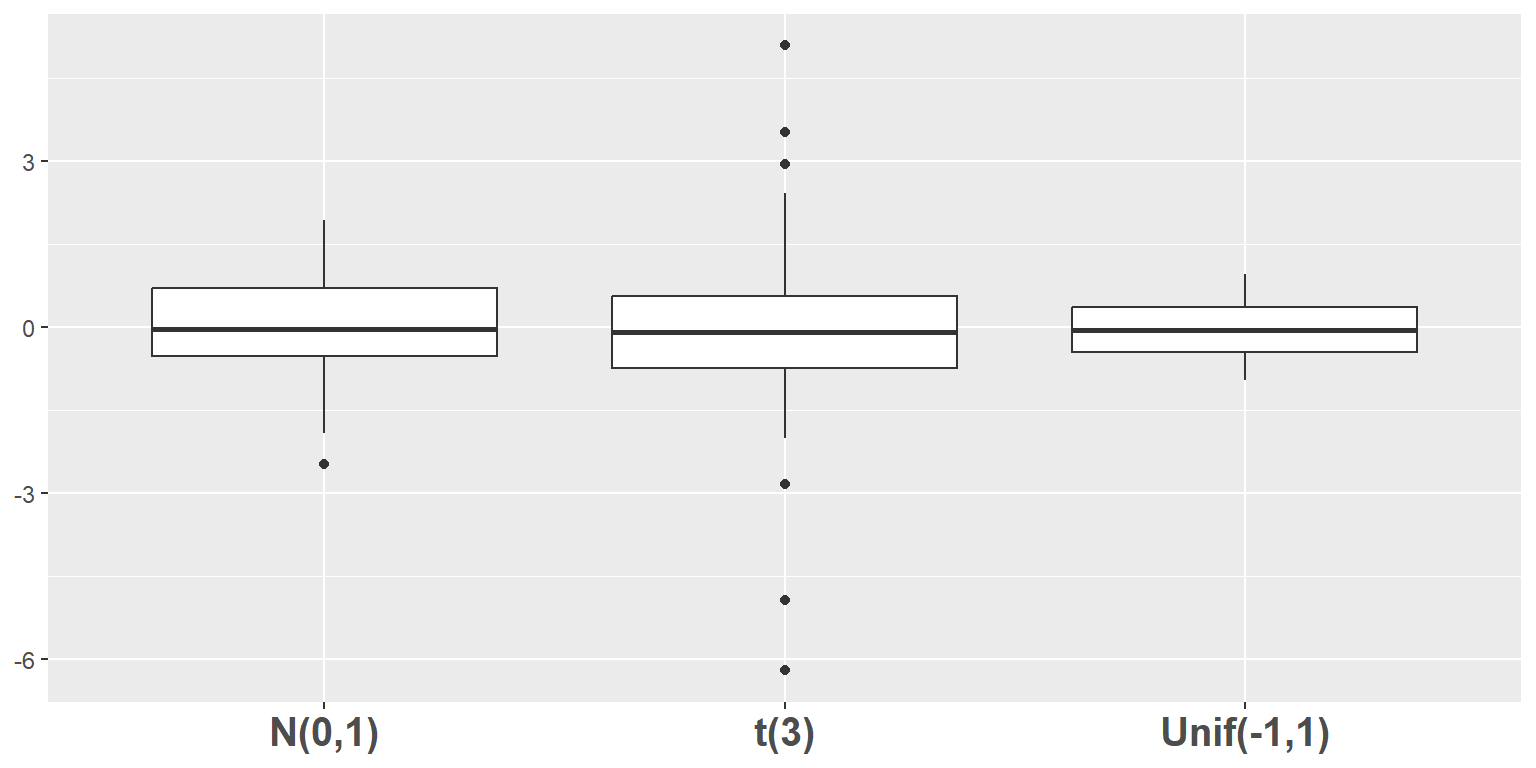
나란히 서 있는 상자그림

그림 9.48: 나란히 서 있는 상자그림

두 번째 경우로 하나의 연속형 변수가 하나 또는 그 이상의 요인에 의하여 몇 개의 그룹으로 구분되는 경우를 살펴보자. 이런 경우 함수 geom_boxplot()에 시각적 요소 x에는 요인을, y에는 연속형 변수를 매핑하면 수직방향의 나란히 서 있는 상자그림이 작성되고, y에 요인을 x에 연속형 변수를 매핑하면 수평방향의 나란히 서 있는 상자그림이 작성된다.

예제로 패키지 ggplot2의 데이터 프레임 mpg의 변수 cyl에 따른 hwy의 분포를 비교해 보자. 변수 cyl이 5인 자료를 제외한 mpg_1을 사용하자.

mpg_1 <- mpg |> filter(cyl!=5)
ggplot(mpg_1, aes(x = factor(cyl), y = hwy)) + 
  geom_boxplot() +
  labs(x = "Number of Cylinders", y = "MPG")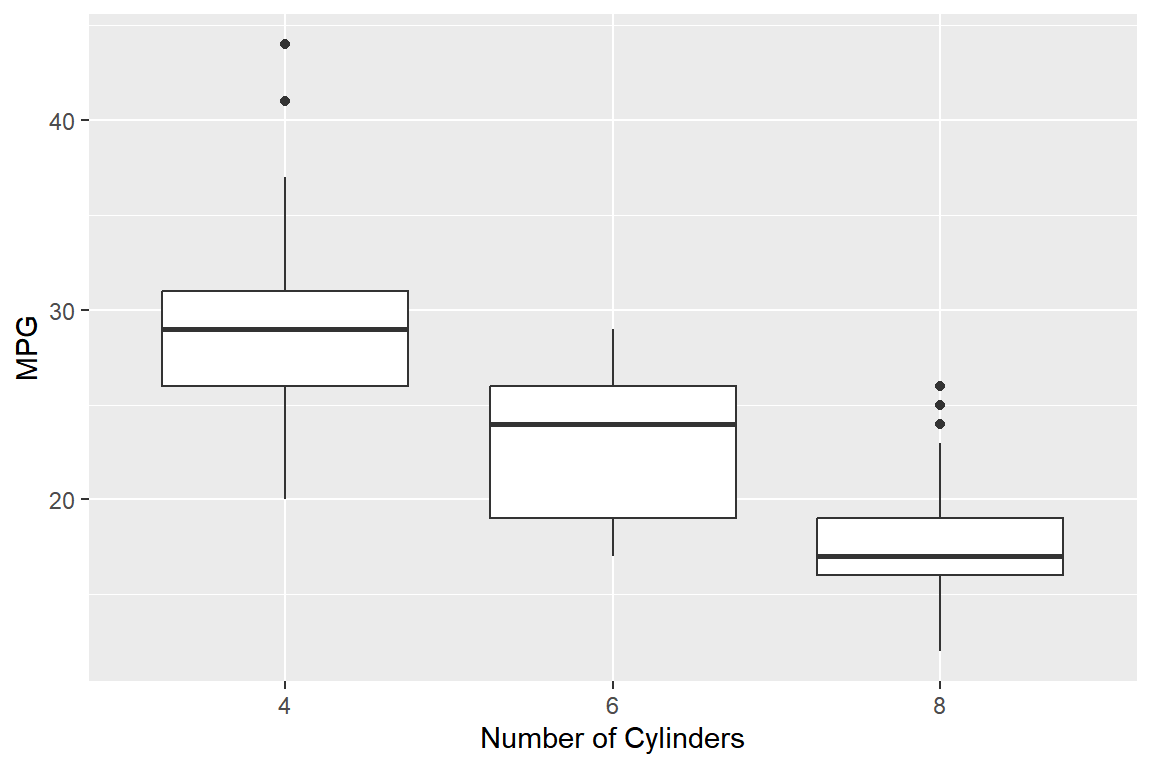
수직방향의 나란히 서 있는 상자그림

그림 9.49: 수직방향의 나란히 서 있는 상자그림 

ggplot(mpg_1, aes(y = factor(cyl), x = hwy)) + 
  geom_boxplot() +
  labs(y = "Number of Cylinders", x = "MPG")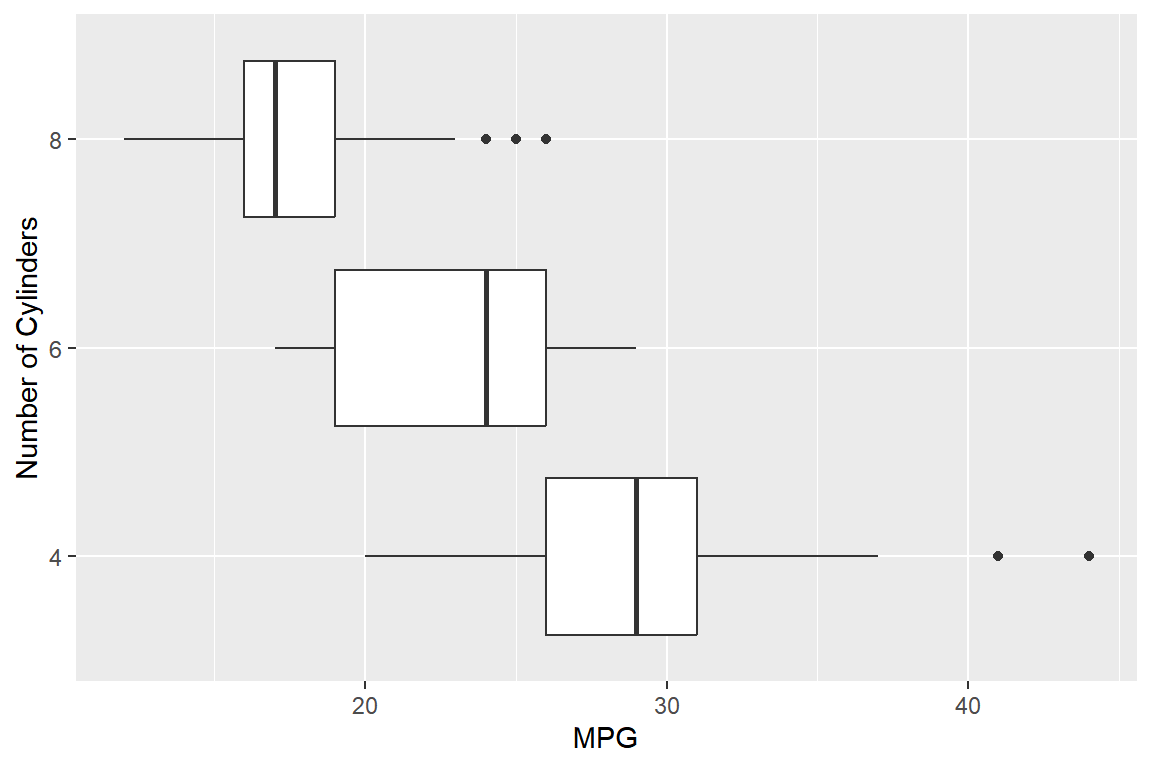
수평방향의 나란히 서 있는 상자그림

그림 9.50: 수평방향의 나란히 서 있는 상자그림

그림 9.49의 상자그림에 점으로 표시된 이상값에 해당되는 자동차를 알아보자. 9.3.2절에서 살펴본 방법을 그대로 적용해 보자.

pp <- ggplot(mpg_1, aes(x = factor(cyl), y = hwy)) + 
  geom_boxplot() 
pp_out <- ggplot_build(pp)[[1]][[1]]$outliers
pp_out
## [[1]]
## [1] 44 44 41
## 
## [[2]]
## numeric(0)
## 
## [[3]]
## [1] 26 26 25 24 25

세 개의 상자그림 중 첫 번째는 3개의 이상값이 있고, 두 번째는 없으며, 세 번째에는 5개의 이상값이 있음을 알 수 있다. 함수 filter()를 사용해서 해당 자동차를 선택한 결과는 다음과 같다.

mpg |> 
  filter((cyl == 4 & hwy %in% pp_out[[1]]) | (cyl == 8 & hwy %in% pp_out[[3]])) |> 
  arrange(desc(hwy)) |> 
  select(1:2, cyl, hwy)
## # A tibble: 8 × 4
##   manufacturer model        cyl   hwy
##   <chr>        <chr>      <int> <int>
## 1 volkswagen   jetta          4    44
## 2 volkswagen   new beetle     4    44
## 3 volkswagen   new beetle     4    41
## 4 chevrolet    corvette       8    26
## 5 chevrolet    corvette       8    26
## 6 chevrolet    corvette       8    25
## 7 pontiac      grand prix     8    25
## 8 chevrolet    corvette       8    24

변수 cyl의 경우에는 실린더의 개수를 나타내는 4, 6, 8이라는 값이 나름의 순서가 있는 것이어서 그 순서대로 상자그림을 배치하는 것이 두 변수의 관계를 이해하는 데 도움이 된다. 그룹변수의 값들이 순서형 요인과 같이 자체적으로 순서가 있는 경우에는 그 순서대로 상자그림을 배치해도 괜찮겠지만, 명목형 요인과 같이 순서에 의미가 없는 경우에는 분석에 도움이 되도록 상자그림을 재배치하는 것이 더 좋을 것이다.

상자그림들을 재배치하려면 함수 reorder()를 사용하여 그룹변수로 사용되는 요인의 수준을 재정렬하면 된다. 먼저 데이터 프레임 mpg의 변수 hwy의 상자그림을 변수 class의 수준별로 작성해 보자.

mpg |> 
  ggplot(aes(x = class, y = hwy)) + geom_boxplot()
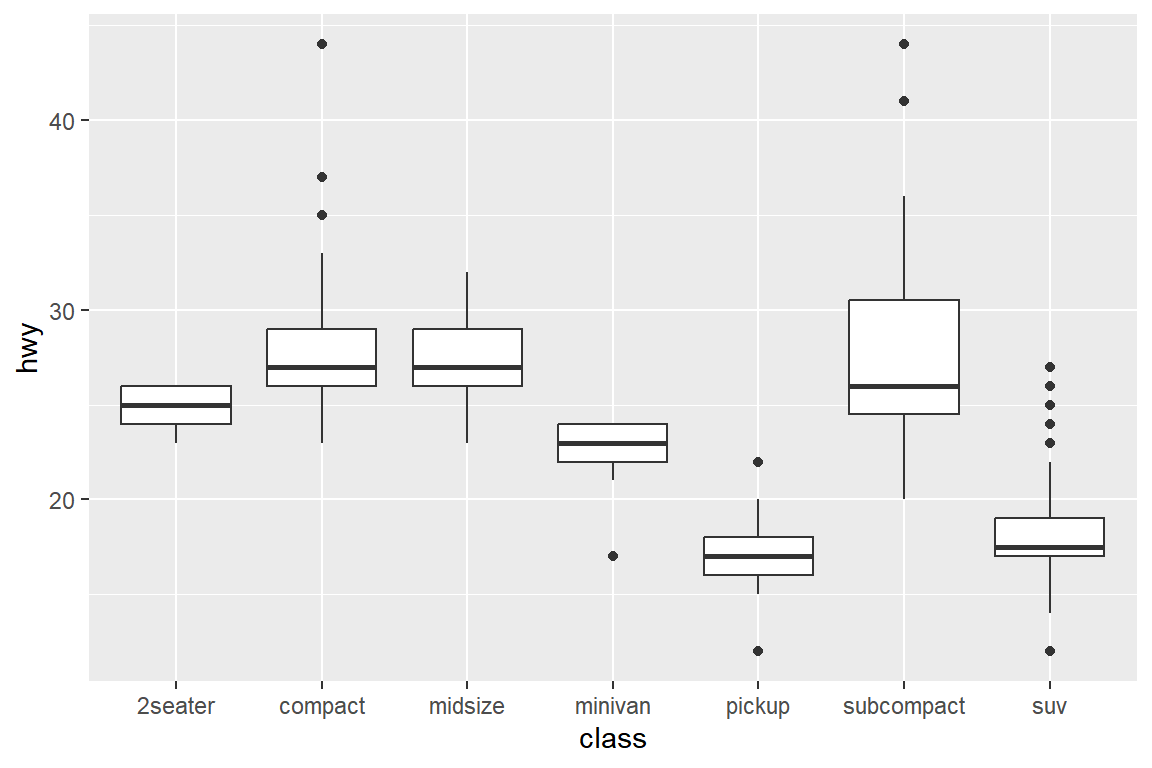
상자그림의 배치 순서

그림 9.51: 상자그림의 배치 순서

상자그림이 변수 class의 알파벳 순서로 배치되어 있다. 이것을 변수 class의 각 그룹별 변수 hwy의 중앙값을 기준으로 재배치하면, 변수 class별로 hwy의 분포를 한 눈에 파악할 수 있게 된다. 함수 reorder()를 사용하여 요인 class의 수준을 변수 hwy의 중앙값을 기준으로 다시 배치하는 방법은 reorder(class, hwy, FUN = median)이 된다.

mpg |> 
  ggplot(aes(x = reorder(class, hwy, FUN = median), y = hwy)) + 
  geom_boxplot() +
  xlab("class")
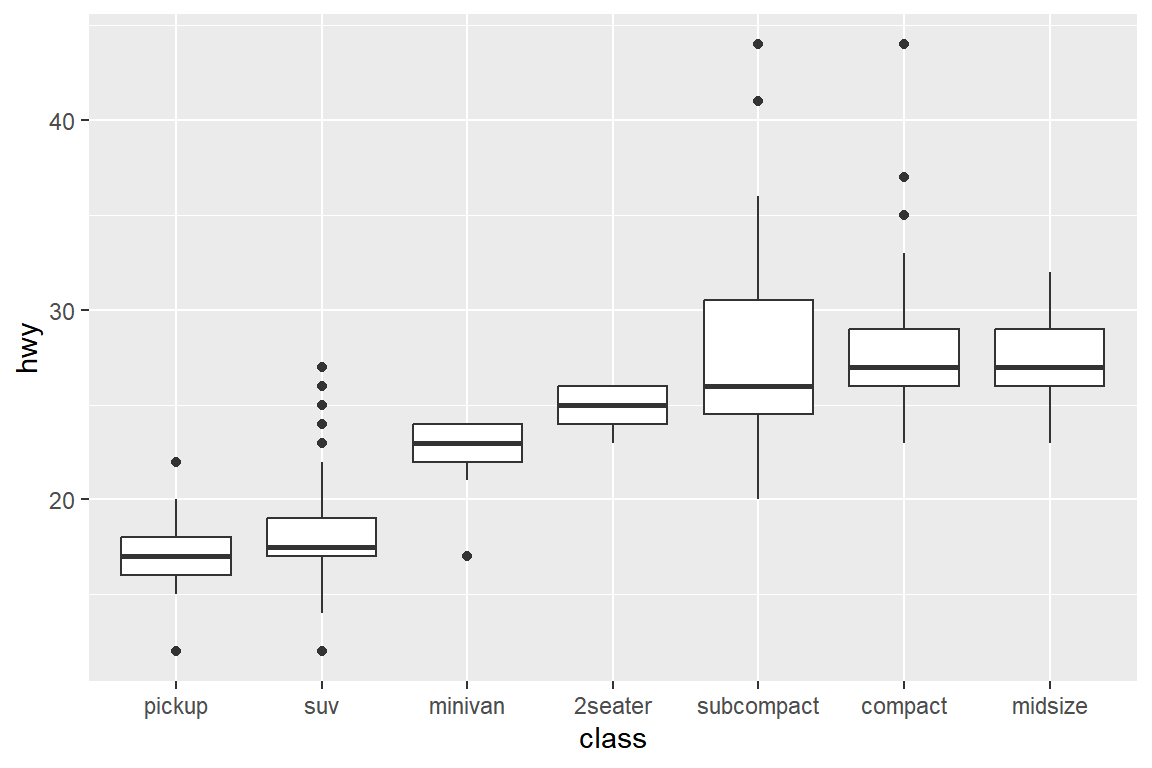
상자그림의 배치 순서 조정

그림 9.52: 상자그림의 배치 순서 조정

\(\bullet\) 나란히 서 있는 violin plot에 의한 그룹 자료의 분포 비교

상자그림과 확률밀도함수 그래프의 조합이라고 할 수 있는 violin plot으로 그룹 자료의 분포를 비교해 보자.

데이터 프레임 iris의 변수 Sepal.Length의 분포가 Species에 따라 어떤 차이가 있는지 살펴보자. 패키지 vioplot의 함수 vioplot()을 사용해서 작성해 보자.

library(vioplot)
vioplot(Sepal.Length ~ Species, data = iris, 
        col = c("lightgreen", "lightblue", "pink"))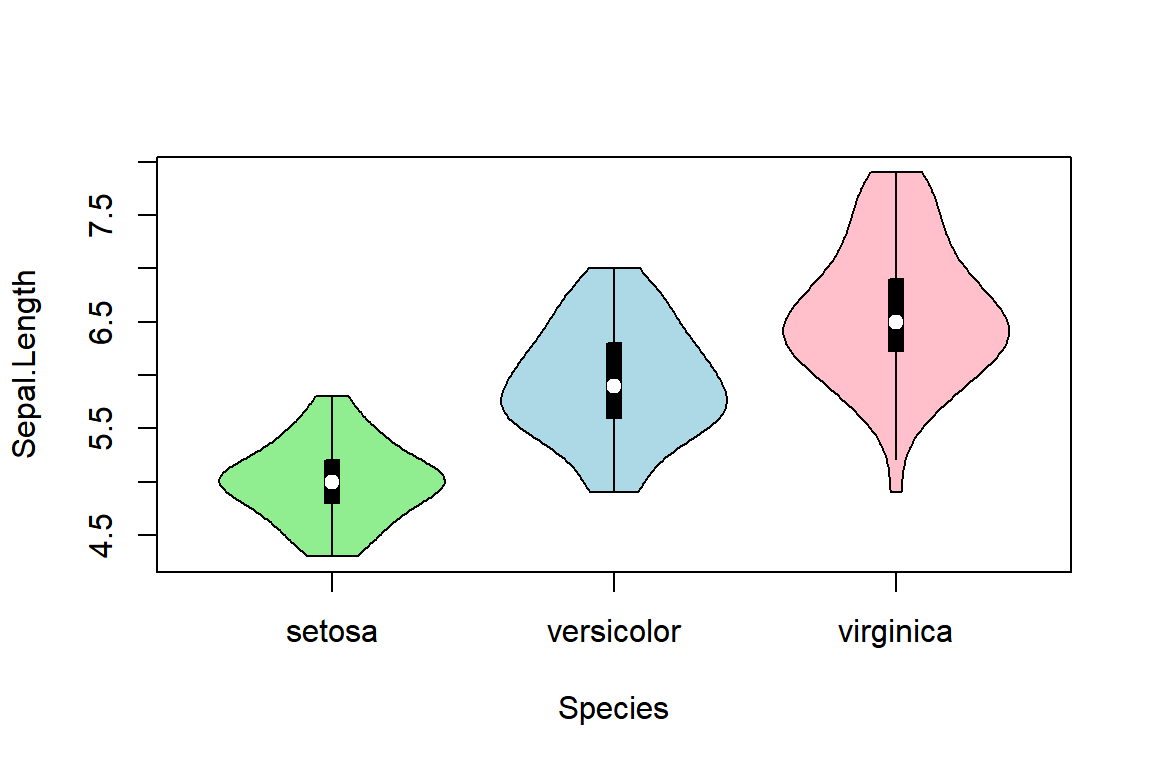
violin plot에 의한 분포 비교

그림 9.53: violin plot에 의한 분포 비교

ggplot2의 함수 geom_violin()을 사용해서 작성한 결과는 다음과 같다.

ggplot(iris, aes(x = Species, y = Sepal.Length)) +
  geom_violin(fill = "skyblue") +
  geom_boxplot(width = 0.1)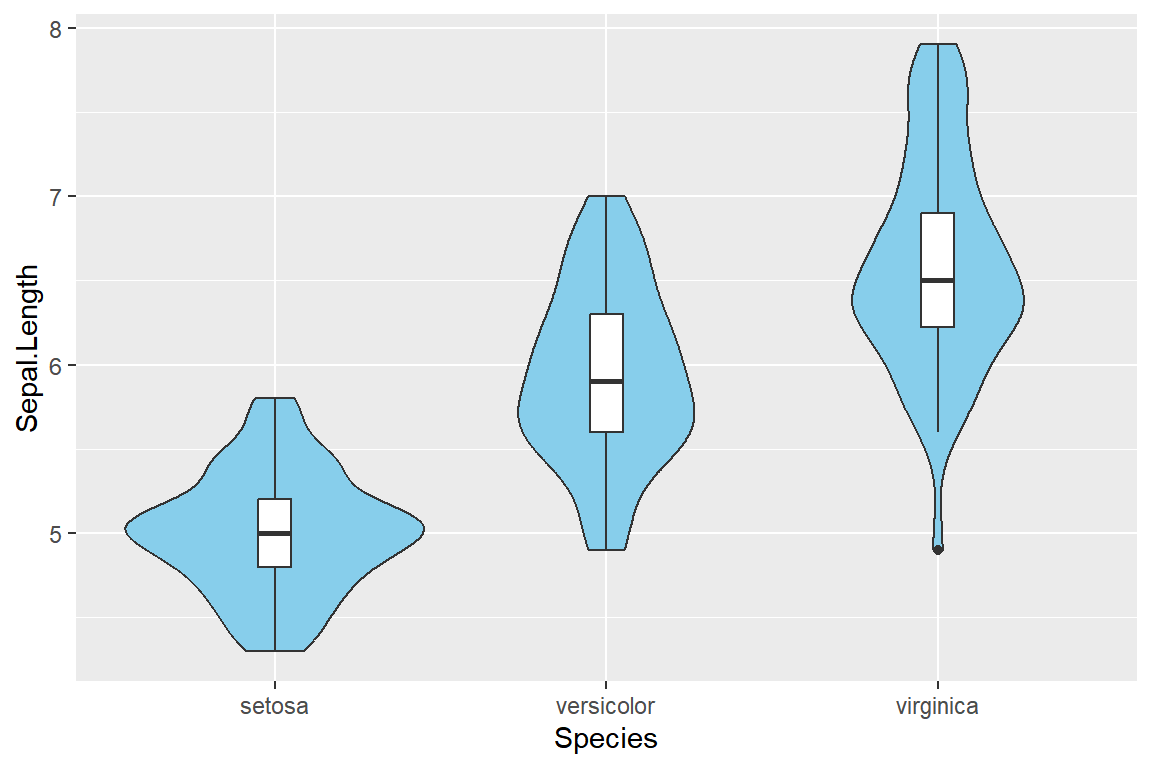
violin plot에 의한 분포 비교

그림 9.54: violin plot에 의한 분포 비교

\(\bullet\) 다중 점그래프에 의한 그룹 자료의 분포 비교

다중 점그래프도 그룹 자료의 분포를 비교하는 데 적합한 그래프라고 할 수 있다. 예제로 패키지 ggplot2의 데이터 프레임 mpg의 변수 cyl에 따른 hwy의 분포를 비교해 보자. 변수 cyl이 5인 자료를 제외한 mpg_1을 사용하자.

mpg_1 <- mpg |> filter(cyl!=5)
ggplot(mpg_1, aes(x = factor(cyl), y = hwy)) +
  geom_dotplot(binaxis = "y", binwidth = 0.5, stackdir = "center") +
  labs(x = "Number of Cylinders", y = "MPG")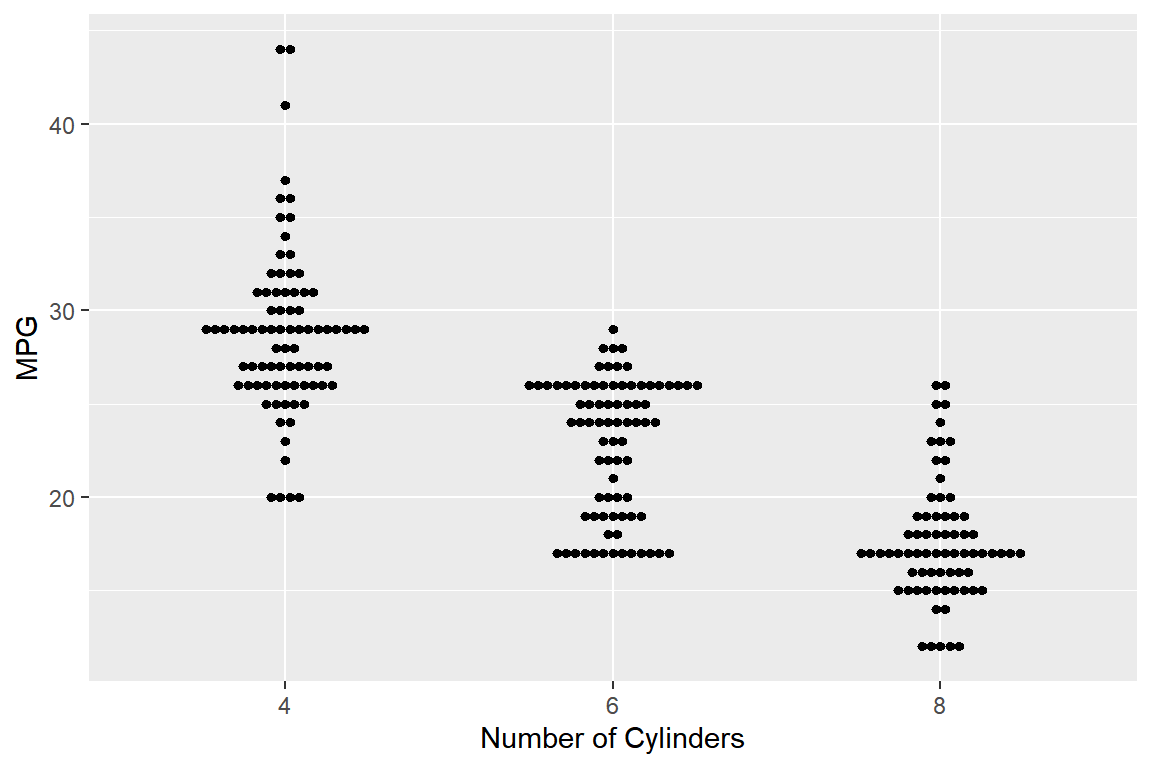
다중 점그래프

그림 9.55: 다중 점그래프

수직방향으로 점그래프를 작성하는 것이므로 구간 설정은 Y축 변수를 대상으로 이루어져야 한다. 옵션 binaxis는 구간 설정 대상이 되는 축을 지정하는 것으로 디폴트는 "x"이다. 점을 쌓아 가는 방향을 결정하는 옵션은 stackdir이다. 가능한 값은 "up", "down", "center"와 "centerwhole“이 있다.

다중 점그래프를 상자그림과 겹쳐서 작성하는 것도 의미가 있는 그래프가 된다. 이 경우에도 상자그림에 outlier.shape = NA를 포함시켜 이상값을 점으로 표시하지 않도록 해야 하며, 상자 내부에 색을 채우지 않도록 fill = NA를 지정할 필요가 있다. 또한 상자의 폭을 줄여 주는 것도 필요하다고 본다.

ggplot(mpg_1, aes(x = factor(cyl), y = hwy)) +
  geom_dotplot(binaxis = "y", binwidth = 0.5, stackdir = "center") +
  geom_boxplot(width = 0.3, outlier.shape = NA,
               color = "red", fill = NA, size = 0.6) +
  labs(x = "Number of Cylinders", y = "MPG")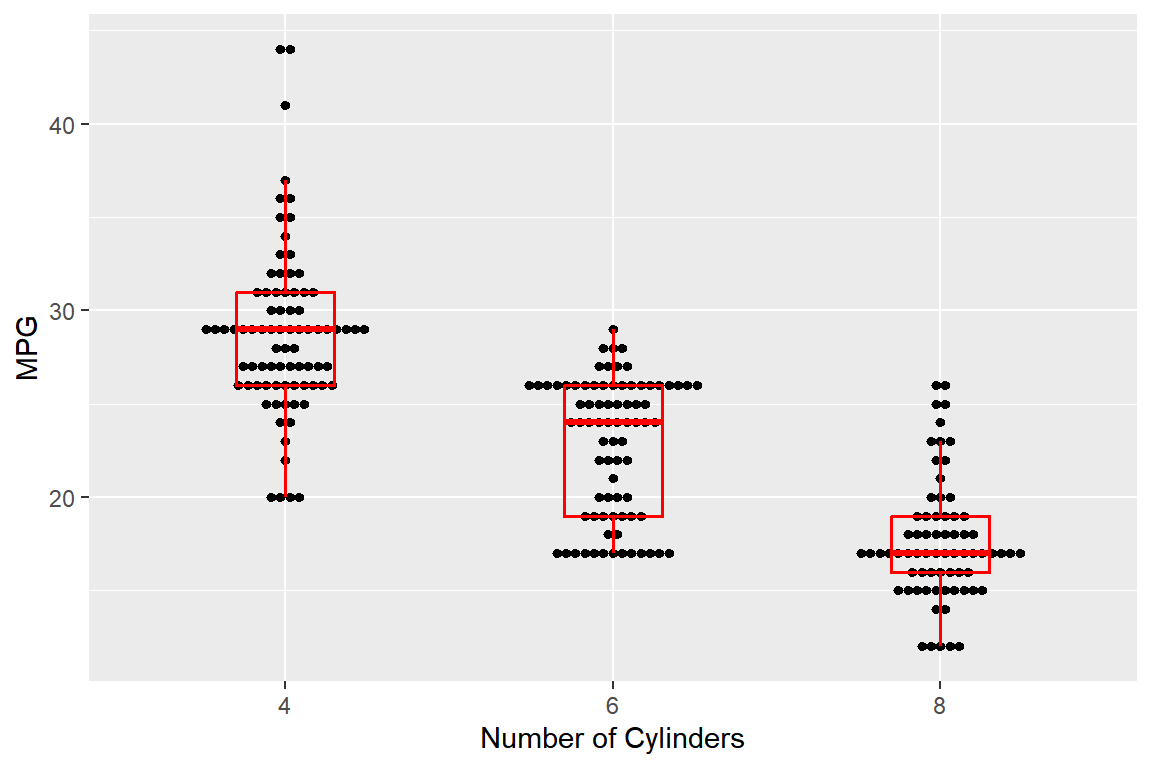
다중 점그래프

그림 9.56: 다중 점그래프

\(\bullet\) 확률밀도함수 그래프에 의한 그룹 자료의 분포 비교

분포의 특징을 가장 세밀하게 표현할 수 있는 그래프가 확률밀도함수 그래프이다. Facet을 이용하여 그룹별밀도함수를 비교하는 것도 의미가 있으며, 하나의 그래프에 겹치게 작성하는 것도 괜찮은 방법이 된다.

예제로 패키지 ggplot2의 데이터 프레임 mpg의 변수 cyl에 따른 hwy의 분포를 비교해 보자. 변수 cyl이 5인 자료를 제외한 mpg_1을 사용하자.

ggplot(mpg_1, aes(hwy)) +
  geom_density() +
  facet_wrap(vars(cyl), ncol = 1) +
  xlim(5,50) + ylab(NULL)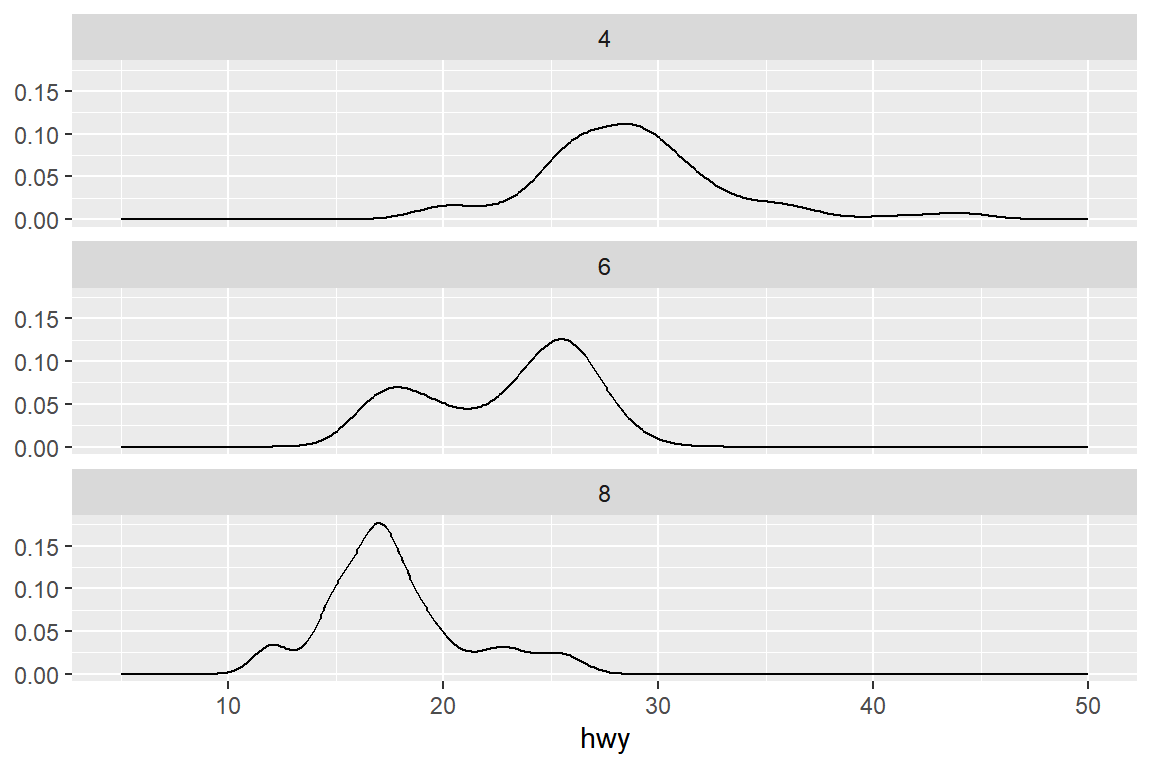
Facet에 의한 그룹별 확률밀도함수의 비교

그림 9.57: Facet에 의한 그룹별 확률밀도함수의 비교

하나의 그래프에 겹치게 작성하는 방법으로써 시각적 요소 fill을 사용하는 것과 시각적 요소 color를 사용하는 것을 생각해 볼 수 있다. 시각적 요소 fill을 사용하면, 확률밀도함수가 색으로 채워지기 때문에 서로 겹쳐져서 가려지는 부분이 있게 된다. 이 문제는 색의 투명도를 높이면 해결된다.

ggplot(mpg_1, aes(x = hwy, fill = factor(cyl))) + 
  geom_density(alpha = 0.2) + 
  xlim(5,50) + labs(y = NULL, fill = "cyl")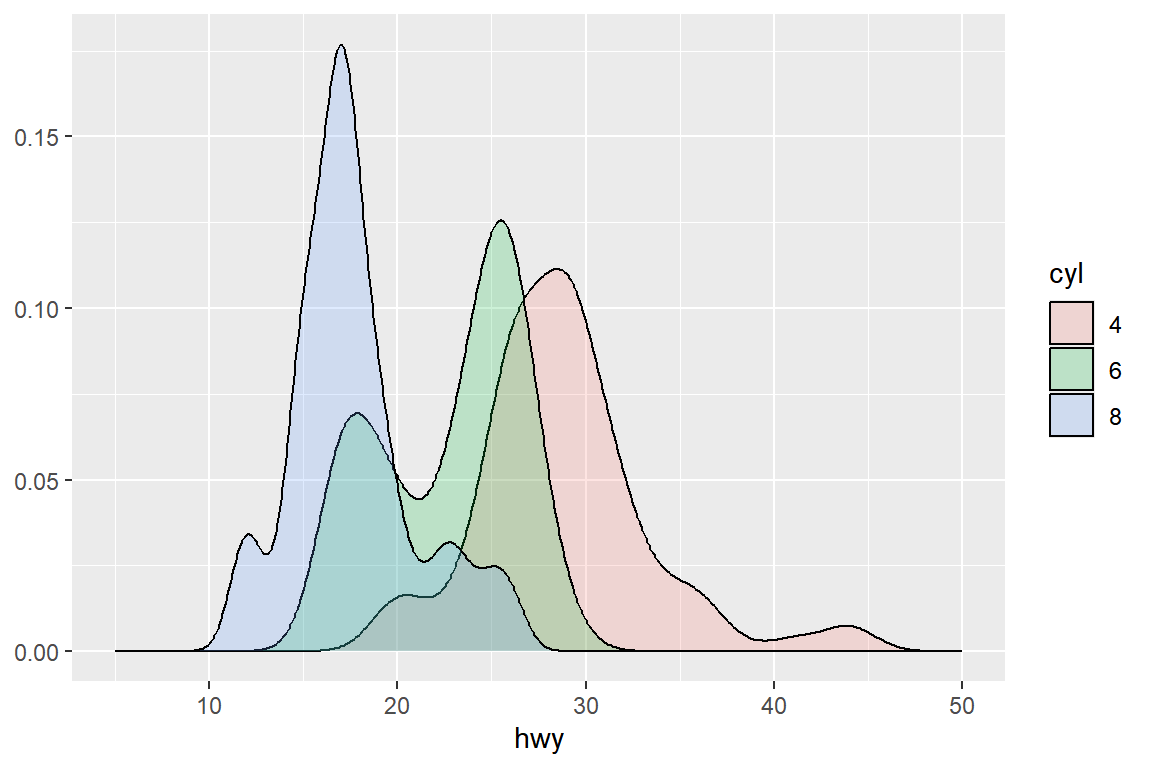
겹쳐 그린 확률밀도함수 그래프

그림 9.58: 겹쳐 그린 확률밀도함수 그래프

시각적 요소 fill 대신 color를 사용하면 서로 다른 색의 선으로만 밀도함수가 그려지는 그래프가 작성된다.

ggplot(mpg_1, aes(x = hwy, color = factor(cyl))) + 
  geom_density(linewidth = 1) + 
  xlim(5,50) + labs(y = NULL, color = "cyl")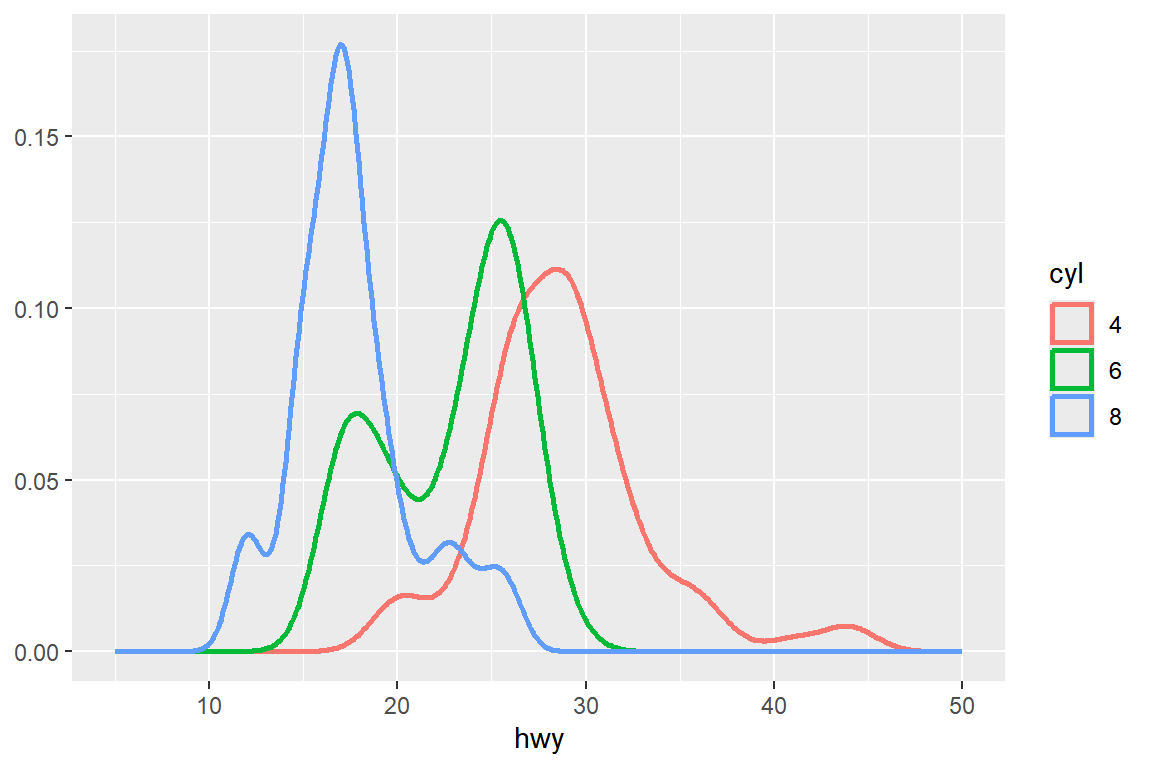
겹쳐 그린 확률밀도함수 그래프

그림 9.59: 겹쳐 그린 확률밀도함수 그래프

그룹별로 작성되는 여러 개의 확률밀도함수를 하나의 그래프에 나타내는 또 다른 방법으로서 추정된 여러 개의 확률밀도함수를 위로 쌓아 올린 그래프와 x 변수의 주어진 값에 대한 각 그룹의 조건부 확률밀도함수를 작성한 그래프가 있다. 먼저 추정된 확률밀도함수를 위로 쌓아 올린 그래프를 작성해 보자. 이 경우에는 각 그룹마다 추정된 확률밀도에 자료의 수를 곱한 값을 사용하여 위로 쌓아 올리는 것이 각 그룹의 확률분포의 형태를 유지하며 통합하는 방법이 된다. 시각적 요소 y에 변수 after_stat(count)를 연결하고, position에 "stack"을 지정하여 그래프를 작성해 보자.

ggplot(mpg_1, aes(x = hwy, fill = factor(cyl))) +
  geom_density(aes(y = after_stat(count)), position = "stack") +
  xlim(5, 50) + labs(y = NULL, fill = "cyl")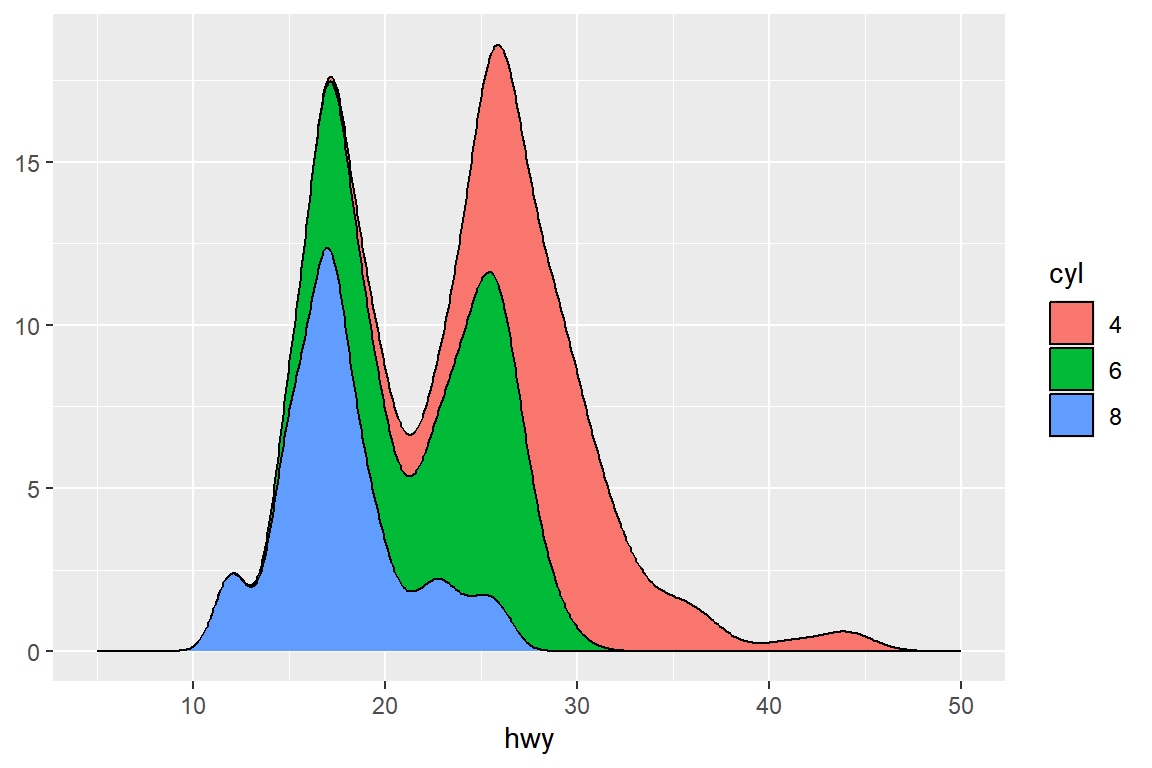
쌓아 올린 확률밀도함수 그래프

그림 9.60: 쌓아 올린 확률밀도함수 그래프

쌓아 올린 확률밀도함수 그래프와는 조금 다른 시각에서 분포를 비교할 수 있는 그래프로서 조건부 확률밀도함수 그래프를 작성해 보자. 이 그래프는 position에 "fill"을 지정하면 작성된다.

ggplot(mpg_1, aes(x = hwy, fill = factor(cyl))) +  
  geom_density(aes(y = after_stat(count)), position="fill") +
  labs(y = NULL, fill = "cyl")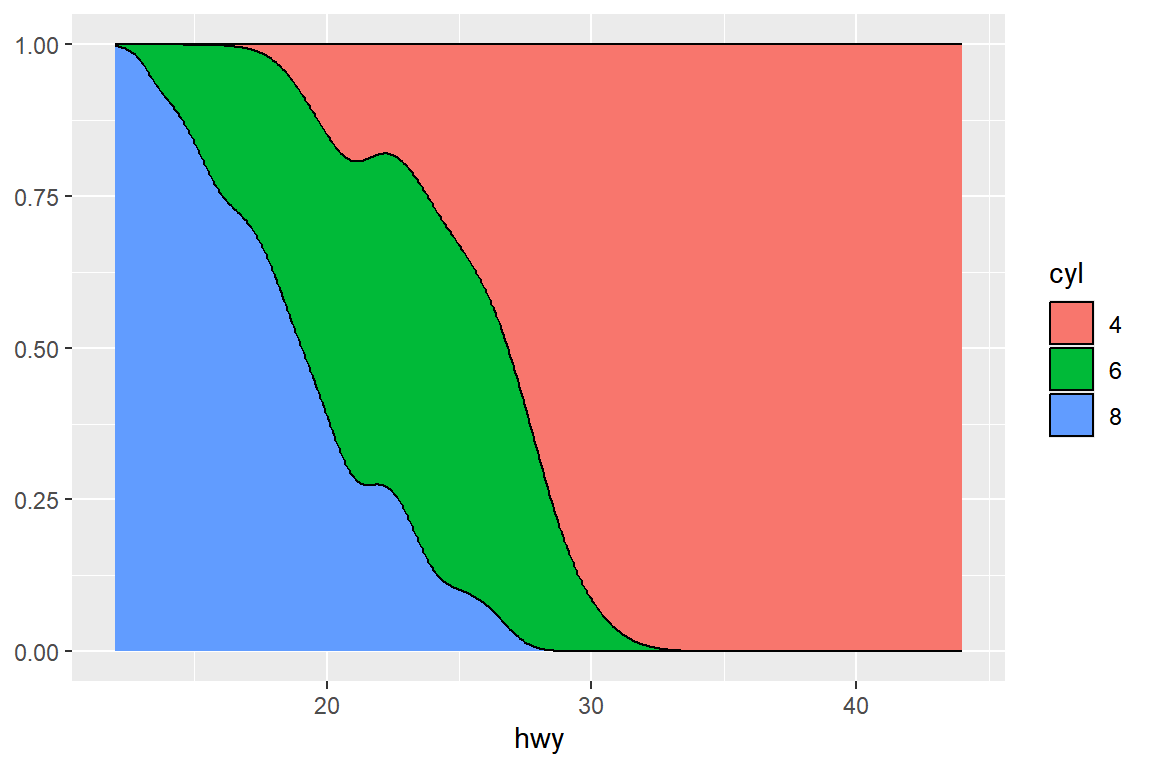
조건부 확률밀도함수 그래프

그림 9.61: 조건부 확률밀도함수 그래프

\(\bullet\) 평균 막대그래프와 error bar에 의한 그룹 자료의 분포 비교

여러 분포의 평균값을 비교할 때 단순히 숫자만을 보여주는 것보다는 그래프로 바꿔서 보여 주는 것이 훨씬 효과적으로 정보를 전달하는 방법이 될 것이다. 그런 면에서 막대그래프는 그룹별 자료의 평균을 비교하는 그래프로서 상당히 효과적으로 사용할 수 있다. Error bar는 분포의 변동을 그래프로 나타내는 기법이다. 따라서 그룹별 평균을 막대그래프로 나타내고, 그 위에 error bar로 분포의 변동 혹은 신뢰구간을 함께 표시해 준다면 많은 정보를 매우 효과적으로 전달할 수 있을 것이다.

예제로 패키지 ggplot2의 데이터 프레임 mpg의 변수 cyl에 따른 hwy의 평균값을 막대그래프로 나타내고, 그 위에 95% 신뢰구간을 error bar의 형태로 추가해 보자. 변수 cyl이 5인 자료는 분석에서 제외하기로 하자.

그래프 작성은 함수 geom_col()과 geom_errorbar()를 사용하는 방법과 함수 stat_summary()에 의한 방법이 있다. 먼저 함수 geom_col()과 geom_errorbar()를 사용해서 작성해 보자. 두 함수로 그래프를 작성하려면, 그룹별 평균 및 신뢰구간의 계산 결과를 데이터 프레임으로 갖고 있어야 한다. 신뢰구간 계산은 함수 ggplot2::mean_cl_normal()로 할 수 있는데, 이 함수는 정규분포 가정에서 모평균의 신뢰구간을 계산하는 Hmisc::smean.cl.normal()을 불러와서 작업한다.

mpg |> 
  filter(cyl != 5) |> 
  group_by(cyl) |> 
  summarise(mean_cl_normal(hwy))
## # A tibble: 3 × 4
##     cyl     y  ymin  ymax
##   <int> <dbl> <dbl> <dbl>
## 1     4  28.8  27.8  29.8
## 2     6  22.8  22.0  23.6
## 3     8  17.6  16.9  18.4

위의 계산 결과로 생성된 변수 y에는 표본평균, ymin에는 신뢰구간 하한, ymax에는 신뢰구간 상한이 각각 입력되었다. 평균막대그래프는 변수 y를 함수 geom_col()에 Y축 변수로 매핑하면 작성되고, Error bar는 함수 geom_errorbar()에는 변수 y, ymin, ymax를 같은 이름의 시각적 요소에 매핑하면 작성된다.

mpg |>
  filter(cyl != 5) |>
  group_by(cyl) |>
  summarise(mean_cl_normal(hwy)) |> 
  ggplot(aes(x = factor(cyl), y = y)) +
  geom_col(fill = "skyblue", width = 0.5) +
  geom_errorbar(aes(ymin = ymin, ymax = ymax), width = 0.2) +
  labs(x = "cyl", y = NULL)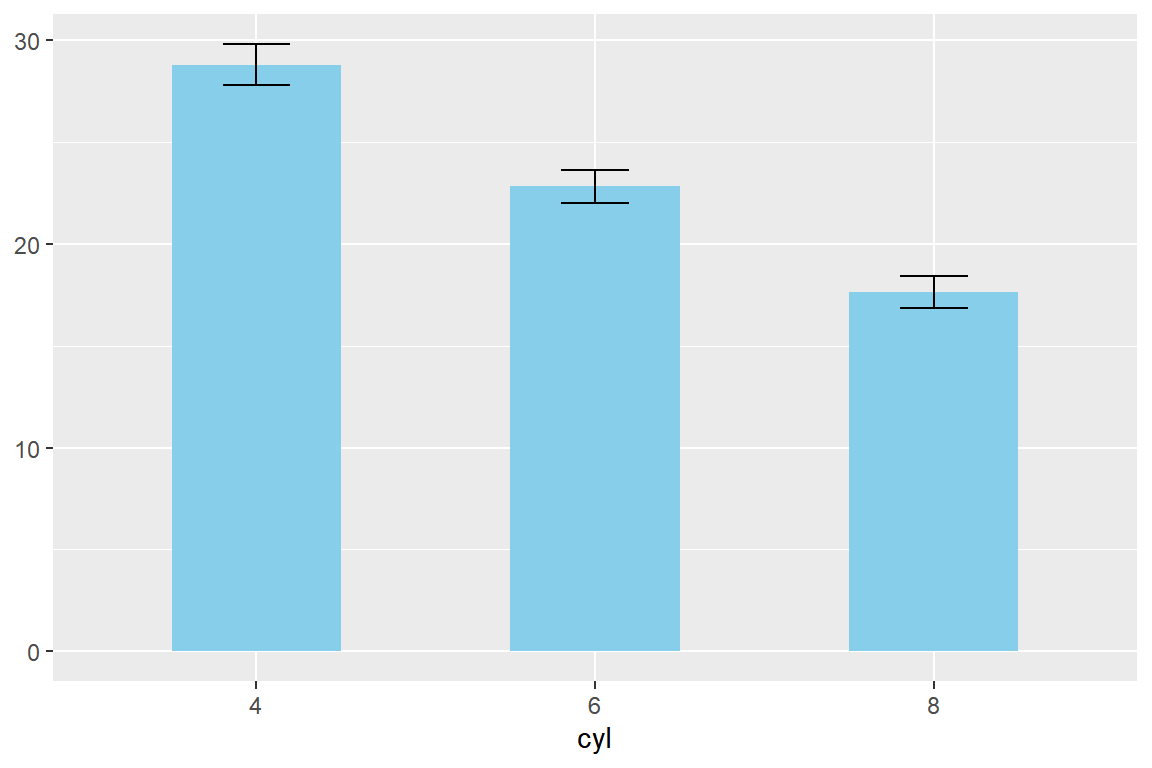
평균 막대 그래프와 error bar

그림 9.62: 평균 막대 그래프와 error bar

이번에는 함수 stat_summary()를 사용해서 작성해 보자. 막대그래프는 fun에 "mean"을, geom에 "bar" 각각 지정하면 작성되고, error bar는 fun.data에 "mean_cl_normal"을, geom에 "errorbar"를 각각 지정하면 된다. fun.data에 지정되는 함수는 반드시 y, ymin, ymax를 계산 결과로 출력하는 함수를 지정해야 한다.

mpg |> 
  filter(cyl != 5) |>
  ggplot(aes(x = factor(cyl), y = hwy)) +
  stat_summary(fun = "mean", geom = "bar", fill = "steelblue", width = 0.5) +
  stat_summary(fun.data = "mean_cl_normal", geom = "errorbar", width = 0.2, 
               color = "red", linewidth = 1) +
  labs(x = "cyl", y = NULL)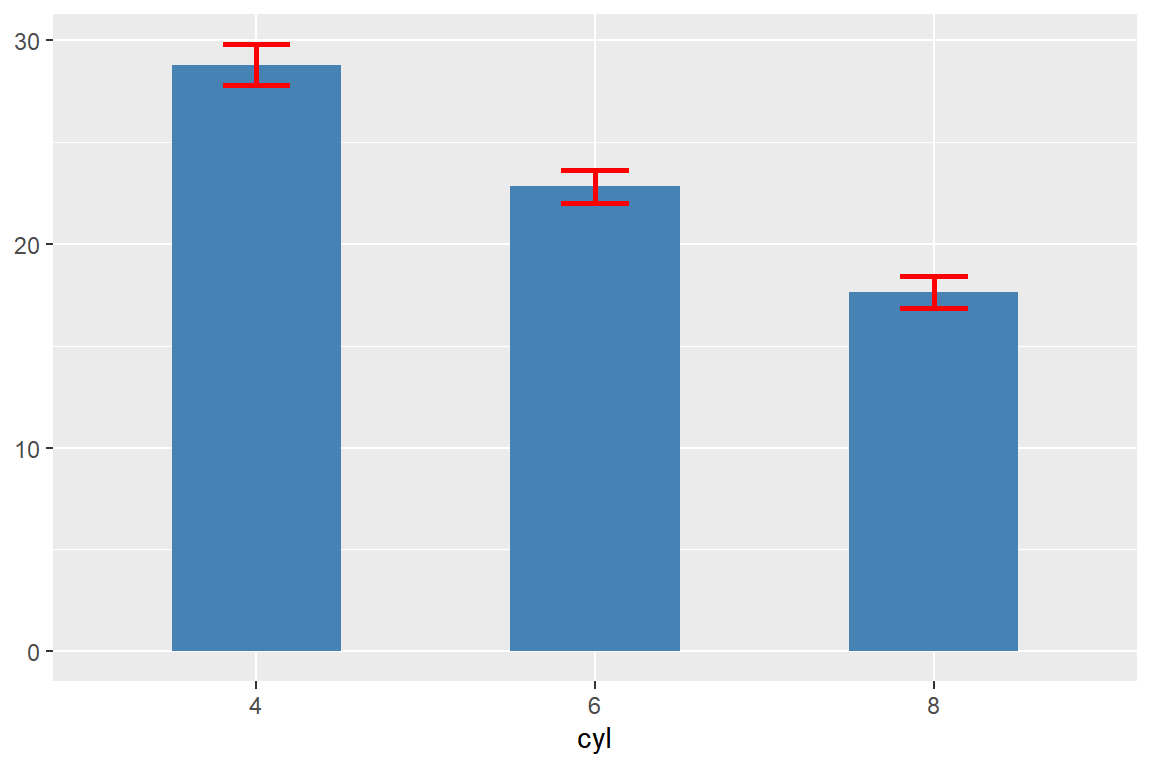
평균 막대 그래프와 error bar

그림 9.63: 평균 막대 그래프와 error bar

9.4.2 연속형 변수의 관계 탐색을 위한 그래프

두 연속형 변수의 관계를 탐색할 때 가장 많이 사용되는 그래프는 산점도일 것이다. 산점도를 확인해 보면 두 변수의 관계를 시각적으로 파악할 수 있는데, 산점도에 두 변수의 회귀직선이나 비모수 회귀곡선 등을 추가하면 관계 파악에 더 도움이 된다. 대규모 자료의 산점도를 작성하면 점들이 서로 겹쳐서 관계 탐색이 어려울 때가 있다. 이런 경우 대안으로 X축 자료를 구간으로 구분하여 Y축 자료의 상자그림을 작성할 수 있다. 두 변수의 결합확률밀도함수를 추정하는 것도 두 변수 관계 파악에 유용하게 사용될 수 있다. 산점도행렬은 많은 연속형 변수들의 관계를 파악하는 데 도움이 많이 되는 그래프이다.

1) 다양한 유형의 산점도 작성

\(\bullet\) 기본적인 형태의 산점도

산점도 작성의 예제 자료로 패키지 MASS의 데이터 프레임 Cars93을 사용해 보자. 먼저 변수 Weight와 MPG.highway의 산점도를 작성해 보자.

data(Cars93, package="MASS")
ggplot(Cars93, aes(x = Weight, y = MPG.highway)) +
  geom_point()
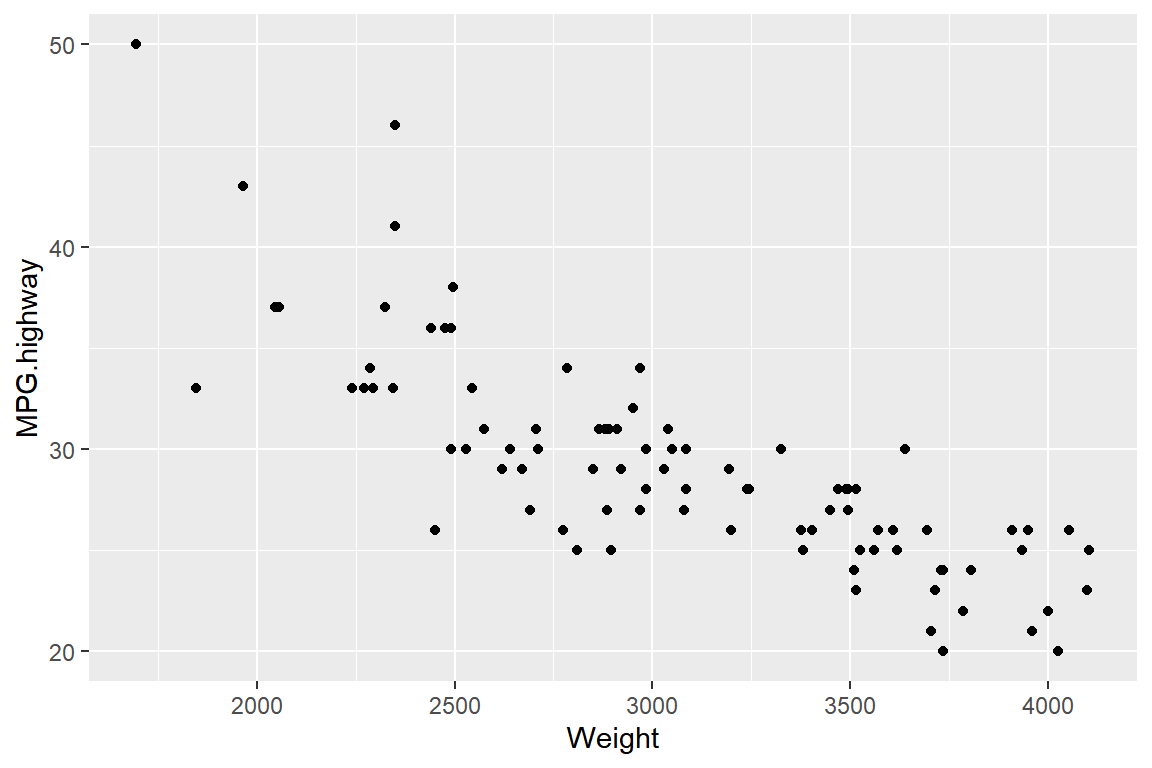
기본적인 형태의 산점도

그림 9.64: 기본적인 형태의 산점도

가장 기본적인 형태의 산점도에 어렵지 않게 변화를 줄 수 있다. 점의 모양(shape = 21)을 내부와 외곽선의 색을 다르게 줄 수 있는 형태로 바꾸고, 크기도 늘리고(size = 3), 점의 내부 색은 파란색(fill = "blue"), 점의 외곽선 색은 빨간색(color = "red"), 그리고 점의 외곽선 두께를 늘려서(stroke = 1.5) 산점도를 작성해 보자. 이 경우 시각적 요소 shape, size, fill, color 등에 특정 변수를 매핑하는 것이 아니고 사용자가 값을 지정하는 것이므로 함수 aes() 밖에서 시각적 요소에 값을 지정해야 한다.

ggplot(Cars93, aes(x = Weight, y = MPG.highway)) +
  geom_point(shape = 21, color = "red", fill = "blue",
             stroke = 1.5, size = 3)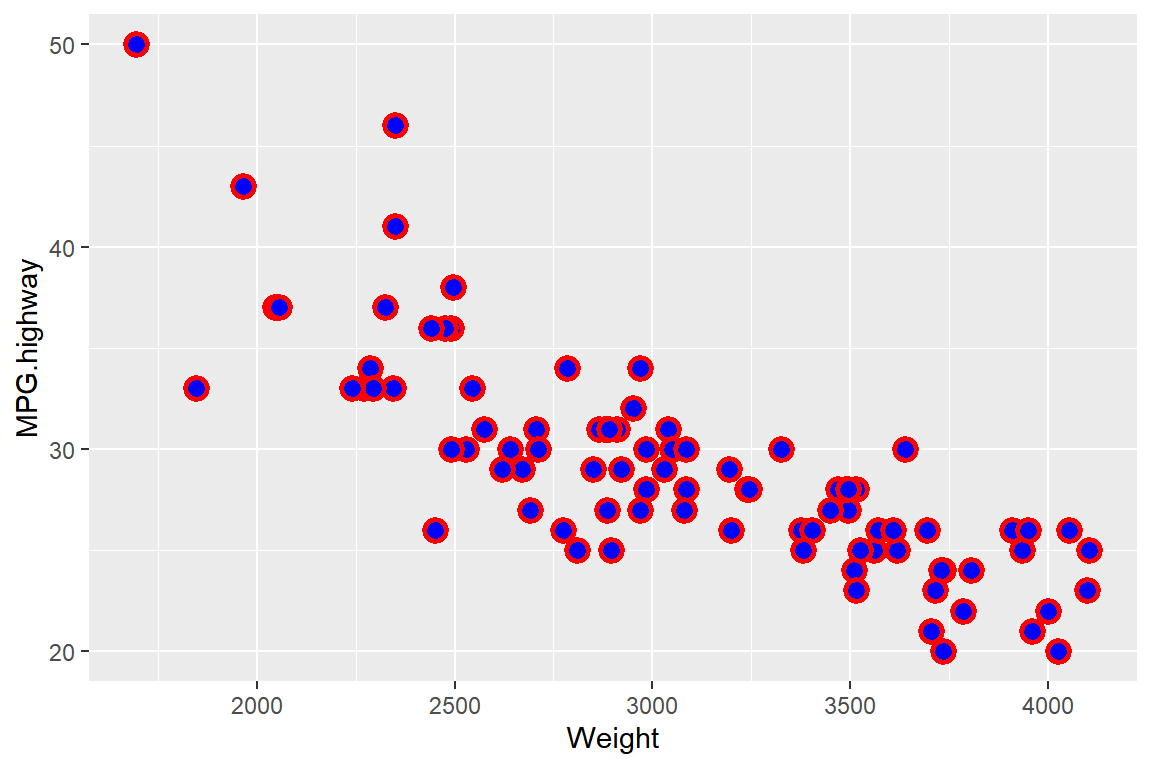
기본적인 형태의 산점도

그림 9.65: 기본적인 형태의 산점도

\(\bullet\) 시각적 요소에 세 번째 변수 매핑

산점도는 두 변수 사이의 관계를 나타내는 그래프이지만, 세 변수 사이의 관계를 나타내는 것도 가능하다. 방법은 두 변수는 시각적 요소 x와 y에 매핑을 하고, 세 번째 변수는 점의 색이나 모양, 크기 등에 매핑을 하는 것이다. 시각적 요소인 점의 색(color)이나 모양(shape), 크기(size) 등을 함수 aes() 안에서 변수와 연결을 하면, 변수에 따라 점의 색이나 모양, 크기 등이 구분되어 산점도가 작성되기 때문에, 세 번째 변수가 두 변수의 관계에 미치는 영향력을 파악할 수 있다. 이 경우 color, shape, size와 같은 시각적 요소에 매핑을 할 변수가 요인인 경우와 숫자형 변수인 경우의 차이점을 살펴보는 것도 중요하다.

변수 Weight와 MPG.highway의 산점도를 작성하되 요인 Origin과 숫자형 변수 EngineSize를 color, shape, size에 각각 매핑한 그래프를 작성해 보자. 먼저 color는 요인과 숫자형 변수 모두 매핑이 가능한 시각적 요소임을 알 수 있다. 하지만 숫자형 변수의 매핑에 사용되는 디풀트 색은 좋은 선택이 아닌 것으로 보이며, 구분이 더 잘 되는 색을 사용할 필요가 있는 것으로 보인다.

library(patchwork)
p1 <- ggplot(Cars93, aes(x = Weight, y = MPG.highway, color = Origin)) +
  geom_point()
p2 <- ggplot(Cars93, aes(x = Weight, y = MPG.highway, color = EngineSize)) +
  geom_point()
p1 + p2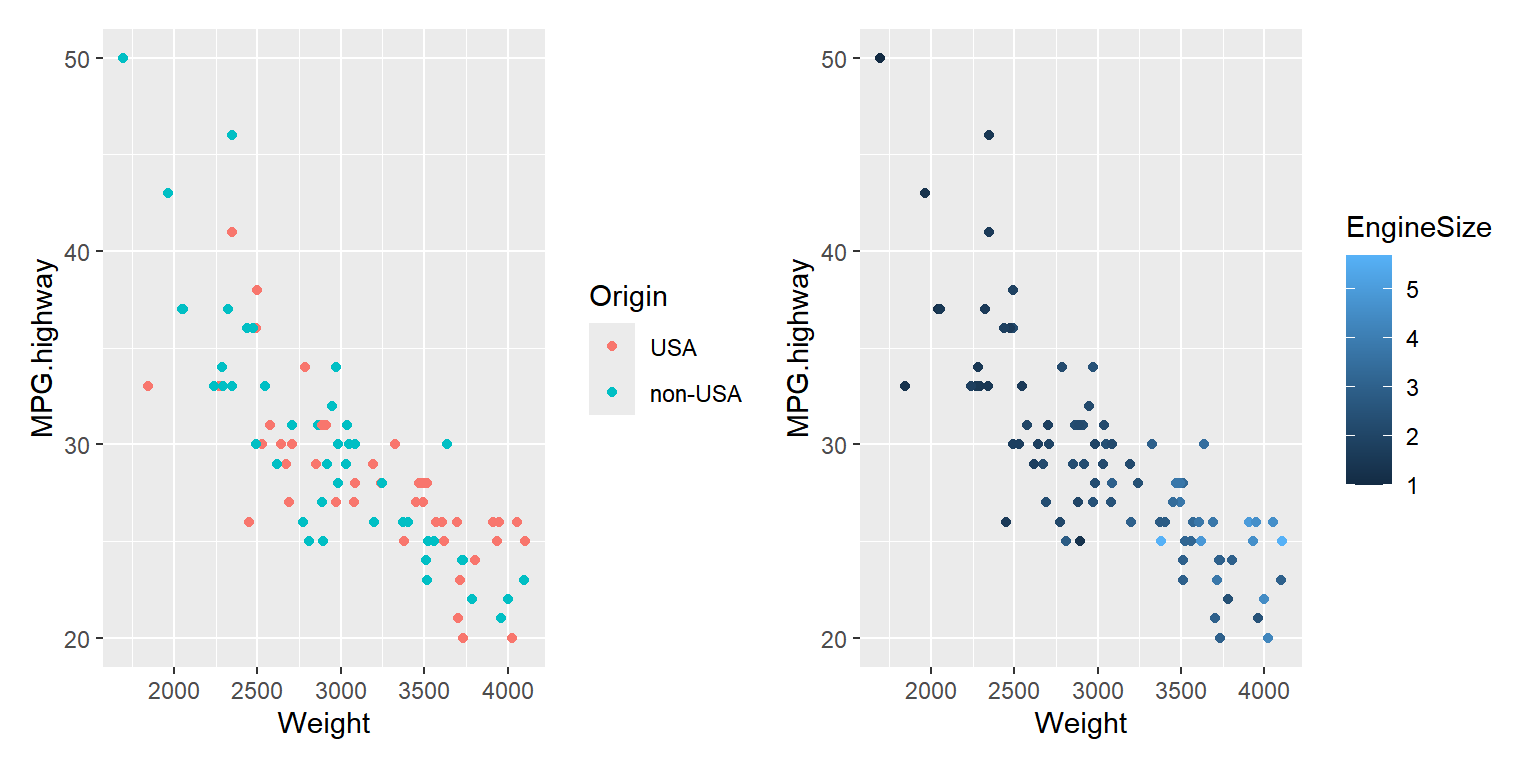
`color`에 요인과 숫자형 변수를 각각 매핑한 산점도

그림 9.66: color에 요인과 숫자형 변수를 각각 매핑한 산점도

이번에는 시각적 요소 shape에 요인과 숫자형 변수를 매핑해 보자.

ggplot(Cars93, aes(x = Weight, y = MPG.highway, shape = Origin)) +
  geom_point()
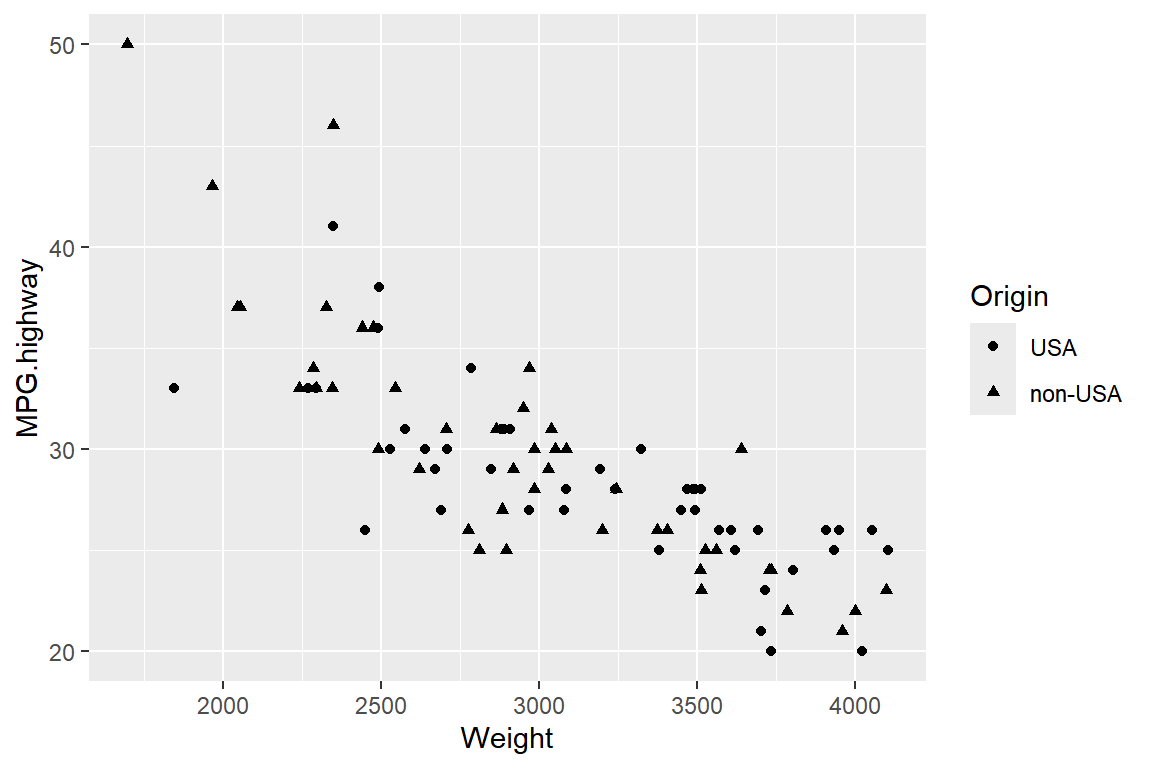
`shape`에 요인을 매핑한 산점도

그림 9.67: shape에 요인을 매핑한 산점도

shape에는 숫자형 변수를 매핑할 수 없다는 것을 알 수 있다.

ggplot(Cars93, aes(x = Weight, y = MPG.highway, shape = EngineSize)) +
  geom_point()
## Error in `geom_point()`:
## ! Problem while computing aesthetics.
## ℹ Error occurred in the 1st layer.
## Caused by error in `scale_f()`:
## ! A continuous variable cannot be mapped to the shape aesthetic.
## ℹ Choose a different aesthetic or use `scale_shape_binned()`.

이번에는 시각적 요소 size에 요인과 숫자형 변수를 매핑해 보자. size에 이산형 변수를 매핑하는 것은 잘못된 정보를 줄 가능성이 있기 때문에 좋은 선택은 아닌 것으로 보인다. 숫자형 변수의 경우에도 미세한 면적 차이를 구분하는 것이 어렵기 때문에 효과적인 정보를 전달하기 어려운 것으로 보인다.

library(patchwork)
p1 <- ggplot(Cars93, aes(x = Weight, y = MPG.highway, size = Origin)) +
  geom_point()
p2 <- ggplot(Cars93, aes(x = Weight, y = MPG.highway, size = EngineSize)) +
  geom_point()
p1 + p2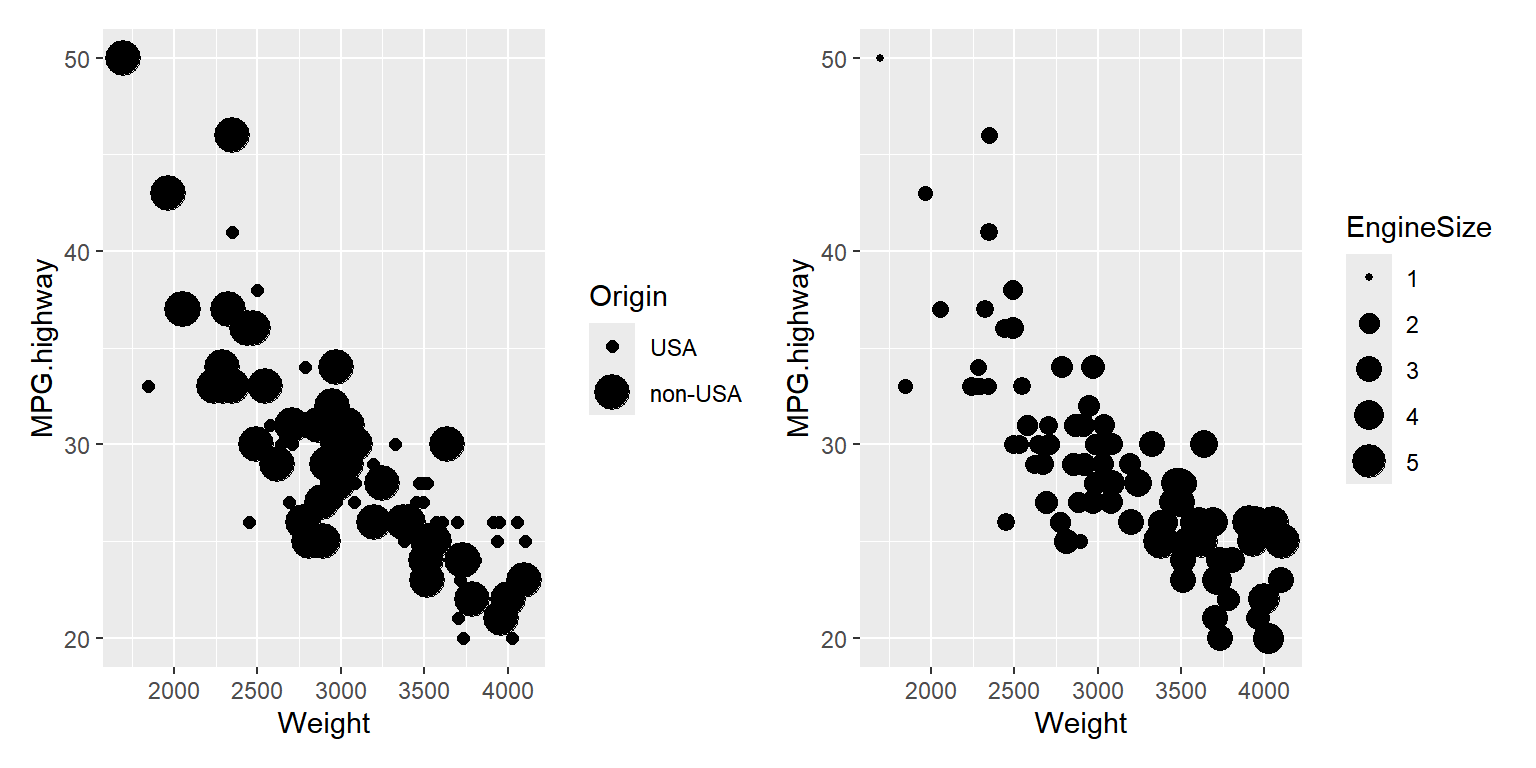
`size`에 요인요인과 숫자형 변수를 각각 매핑한 산점도

그림 9.68: size에 요인요인과 숫자형 변수를 각각 매핑한 산점도

\(\bullet\) 산점도에 회귀직선 추가

산점도만으로 두 변수의 관계를 파악하는 것보다 회귀직선이나 비모수 회귀곡선 등을 추가하는 것이 훨씬 더 효과적일 수 있다. 회귀직선의 추가는 함수 geom_smooth()에 선형회귀모형을 의미하는 method = "lm"을 지정하면 된다. 추정된 회귀직선에 신뢰구간이 함께 표현되는 것이 디폴트인데, 회귀직선만 나타내려면 se = FALSE를 입력해야 한다.

p <- ggplot(Cars93, aes(x = Weight, y = MPG.highway)) + geom_point()
p1 <- p + geom_smooth(method = "lm")
p2 <- p + geom_smooth(method = "lm", se = FALSE)
p1 + p2
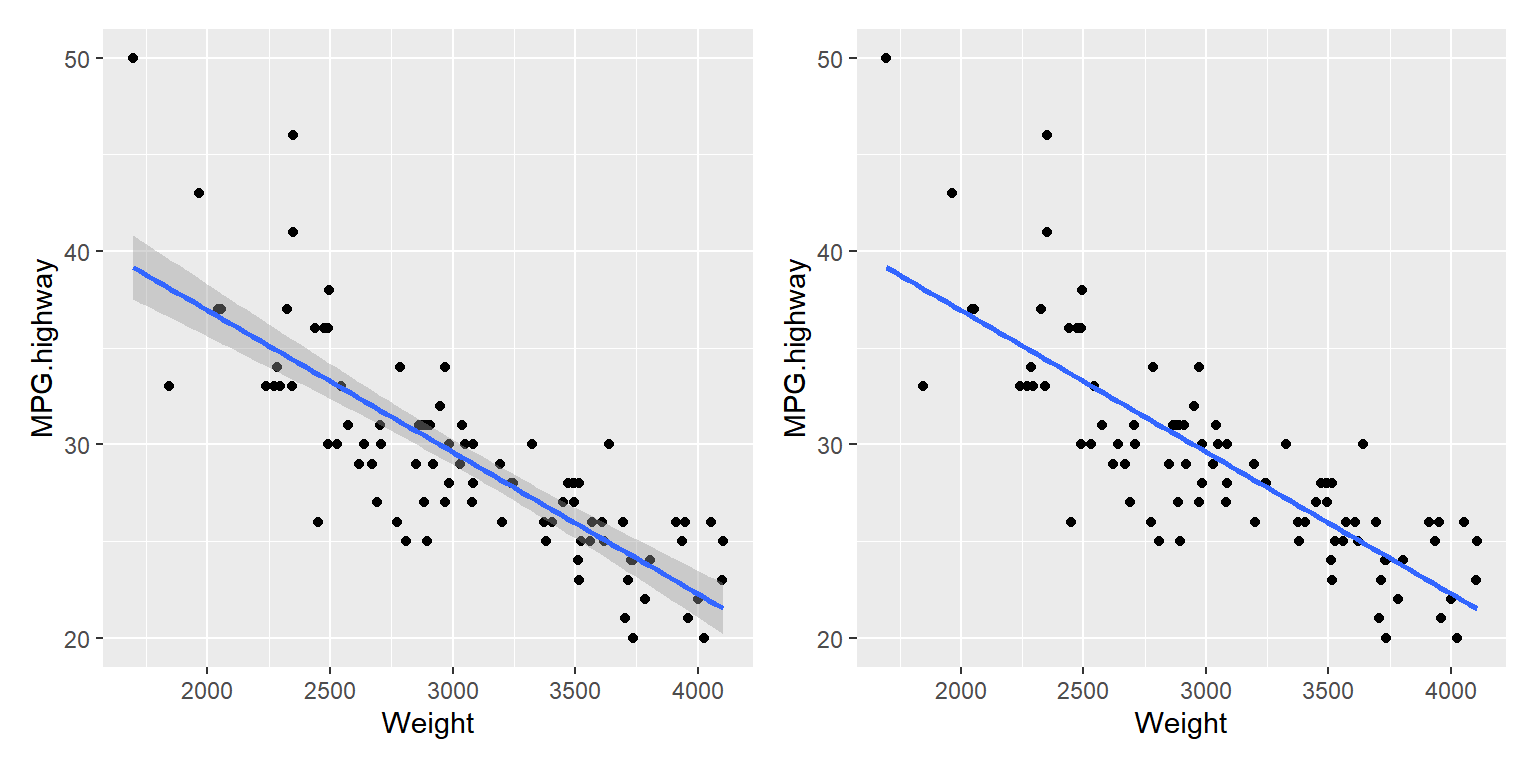
회귀직선을 산점도에 함께 표시

그림 9.69: 회귀직선을 산점도에 함께 표시

두 변수의 관계를 나타내는 회귀모형으로 가장 많이 사용되는 것이 loess(local regression)이라고 불리는 국소다항회귀모형이다. 비모수 회귀모형으로 분류되고 있으며, 자료의 개수가 너무 크지 않는 경우에 가장 무난하게 사용할 수 있는 분석 도구이다. 함수 geom_smooth()에서 디폴트로 적용되는 회귀모형이며, 신뢰구간을 포함하여 표시되는 것이 디폴트이다.

p1 <- p + geom_smooth()
p2 <- p + geom_smooth(se = FALSE)
p1 + p2
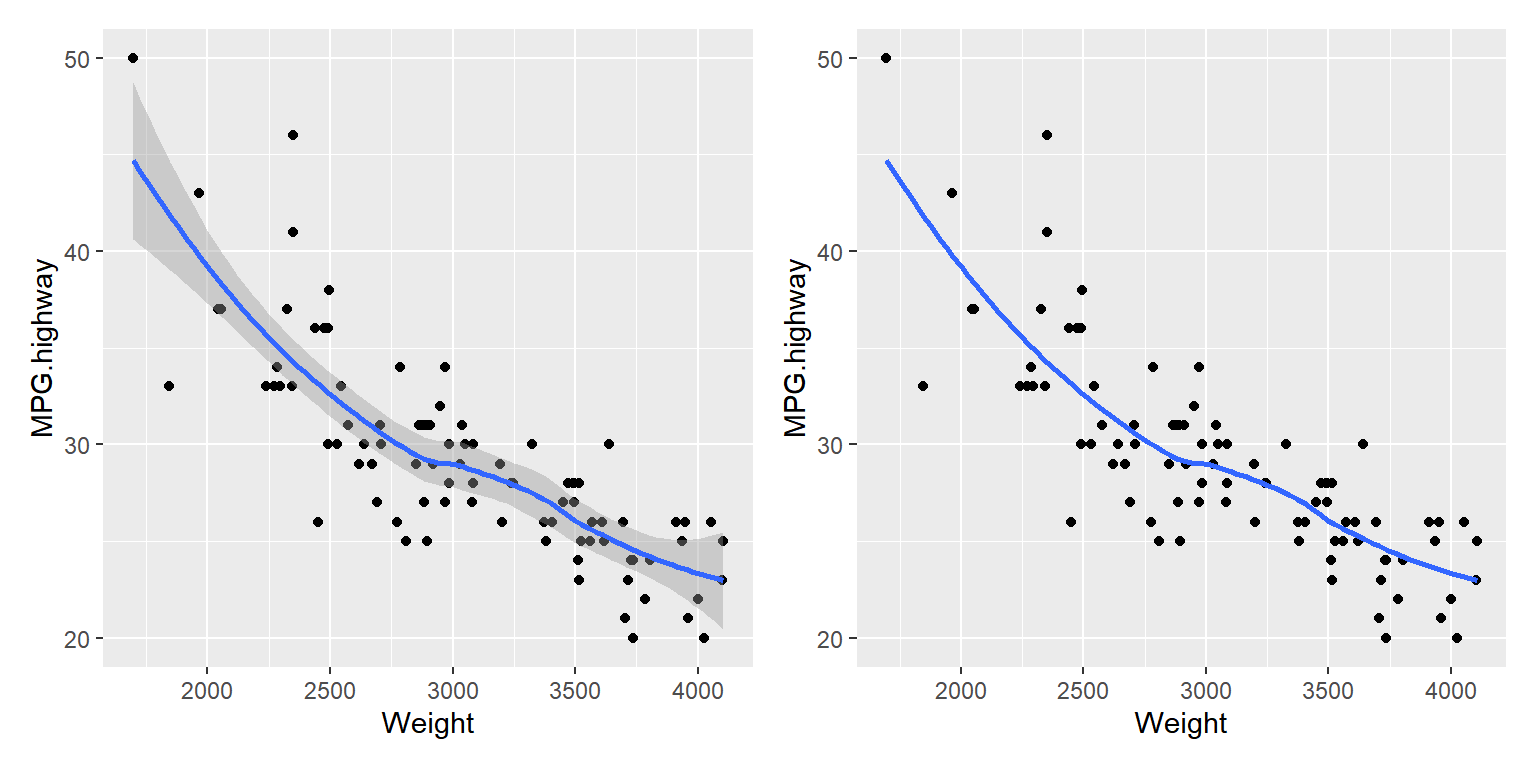
국소회귀곡선을 산점도에 함께 표시

그림 9.70: 국소회귀곡선을 산점도에 함께 표시

선형회귀모형은 두 변수 \(X\) 와 \(Y\) 의 관계를 \(Y=\beta_{0}+\beta_{1}X+\epsilon\) 같이 미리 설정하고, 자료를 근거로 회귀함수의 계수 \(\beta_{0}\) 와 \(\beta_{1}\) 을 추정하여 \(X\) 변수의 전체 범위에서 두 변수의 관계를 수식으로 표현하는 방식이다. 회귀계수는 함수 lm()으로 추정된다.

이에 반하여 국소다항회귀모형은 두 변수의 관계를 미리 설정하지 않으면서 \(X\) 변수의 개별 값에 대하여 회귀함수의값을 각각 추정하는 방식이다. 개별 \(X\) 변수값에 대한 회귀함수의 추정은 가까운 자료만을 대상으로 가중 다항회귀모형을 적합함으로써 이루어지며, 함수 loess()로 추정된다

이번에는 선형회귀직선과 국소회귀곡선을 산점도에 함께 나타내 보자. 두 종류의 선을 다른 색으로 표시하고 범례를 추가해야 하는데, 그래프에 범례(legend)를 추가하는 방법은 5.4절에서 살펴보았다. 시각적 요소 color에 범례의 라벨로 사용할 문자열을 매핑해 보자.

ggplot(Cars93, aes(x = Weight, y = MPG.highway)) +
  geom_point() +
  geom_smooth(aes(color = "lm"), method = "lm", se = FALSE) +
  geom_smooth(aes(color = "loess"), se = FALSE) +
  labs(color = "Method")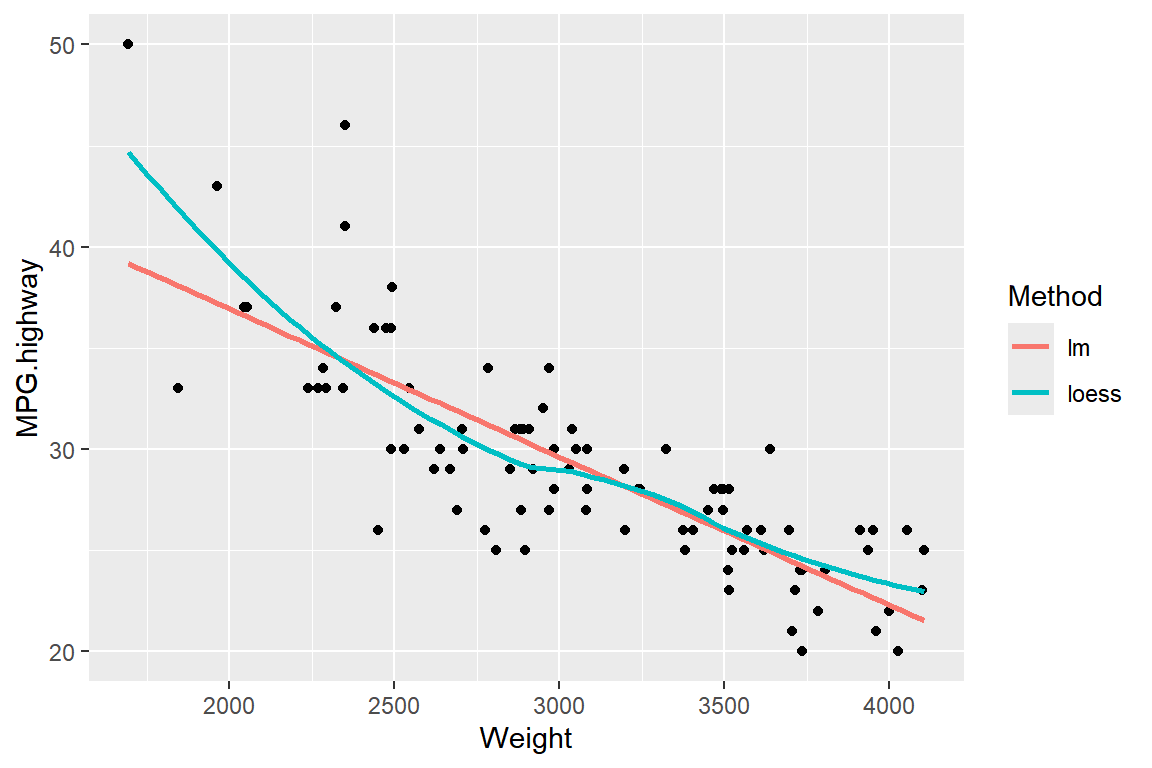
선형회귀직선과 국소회귀곡선을 산점도에 함께 표시

그림 9.71: 선형회귀직선과 국소회귀곡선을 산점도에 함께 표시

\(\bullet\) 산점도에 수평선, 수직선 추가

산점도에는 회귀직선뿐만 아니라 수평선과 수직선도 추가할 수 있다. 수평선의 추가와 수직선의 추가는 각각 함수 geom_hline(yintercept)와 함수 geom_vline(xintercept)으로 할 수 있으며, 직선의 추가는 함수 geom_abline(slope, intercept)으로 할 수 있다.

변수 Weight와 MPG.highway의 산점도에 두 변수의 선형회귀직선을 추가하고, 두 변수의 평균값에 해당하는 위치에 수직선과 수평선을 각각 추가해 보자.

ggplot(Cars93, aes(x = Weight, y = MPG.highway)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  geom_vline(aes(xintercept = mean(Weight)), color = "red") +
  geom_hline(aes(yintercept = mean(MPG.highway)), color = "darkgreen" )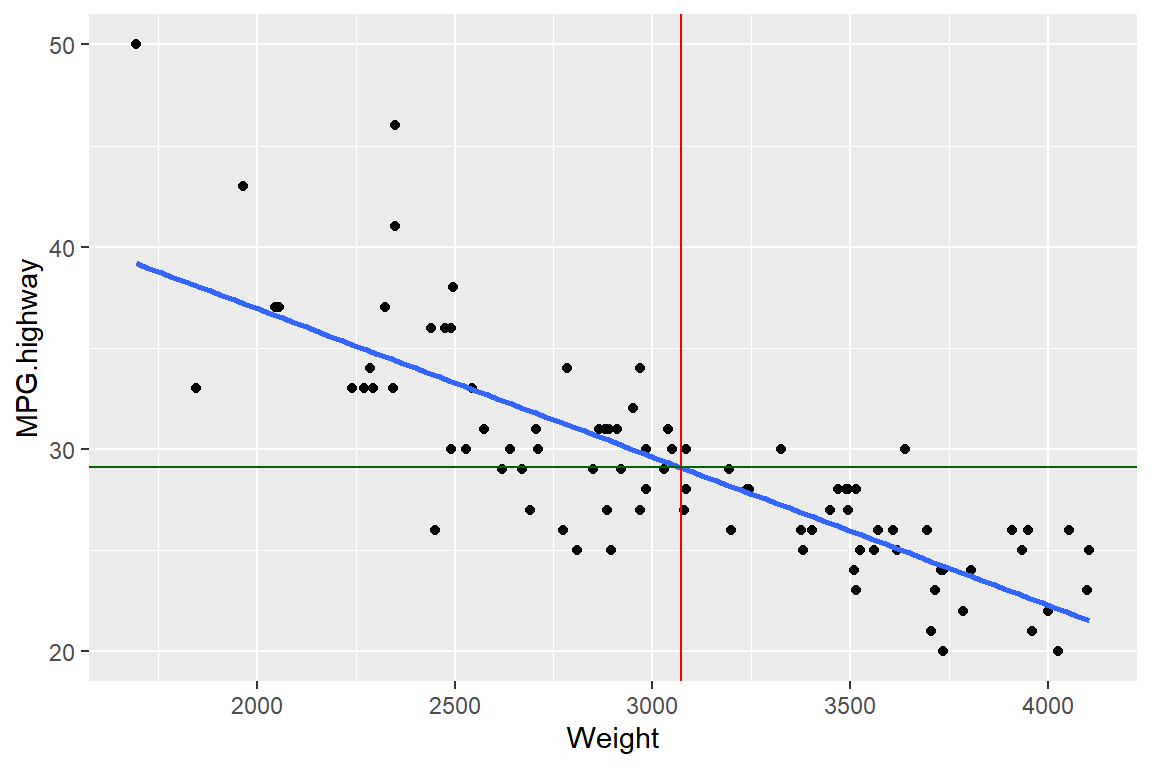
산점도에 수직선과 수평선 추가

그림 9.72: 산점도에 수직선과 수평선 추가

\(\bullet\) 산점도에 그룹별 회귀직선 추가

산점도의 점이 그룹변수의 값에 따라 색이나 모양이 구분되어 있는 경우, 각 그룹별 자료만을 대상으로 추정된 회귀직선을 추가해 보자. 변수 Weight와 MPG.highway의 산점도를 요인 Origin에 따라 점의 색을 구분하고, 각 그룹별 회귀직선을 추정하여 추가해 보자.

ggplot(Cars93, aes(x = Weight, y = MPG.highway, color = Origin)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)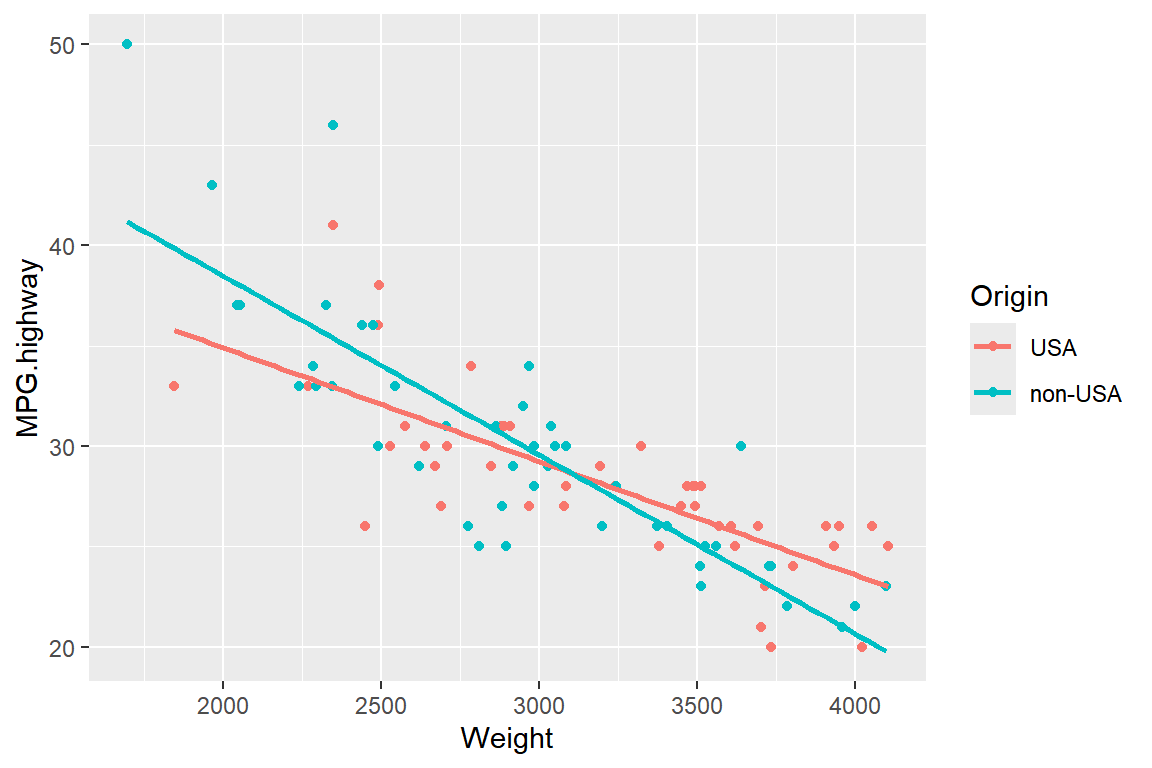
그룹별 회귀직선의 추가

그림 9.73: 그룹별 회귀직선의 추가

\(\bullet\) 산점도의 점에 라벨 추가

산점도에서 특정 조건을 만족하는 점에 라벨을 붙이게 되면 자료의 특성을 파악하는 데 중요한 그래프가 될 수 있다. 산점도의 점에 라벨을 붙이는 작업은 5.4절에서 살펴보았듯이 함수 geom_text()로 할 수 있는데, 시각적 요소 label에 라벨의 내용이 되는 문자형 변수를 매핑하면 된다.

변수 Weight와 MPG.highway의 산점도에서 변수 MPG.highway가 40을 초과하는 점에 라벨을 붙여 보자. 라벨의 내용은 변수 Manufacturer와 Model의 값을 결합한 것으로 하자.

p <- ggplot(Cars93, aes(x=Weight, y=MPG.highway)) + 
  geom_point() 
p + geom_text(data = filter(Cars93, MPG.highway > 40), 
              aes(label = paste(Manufacturer, Model)))
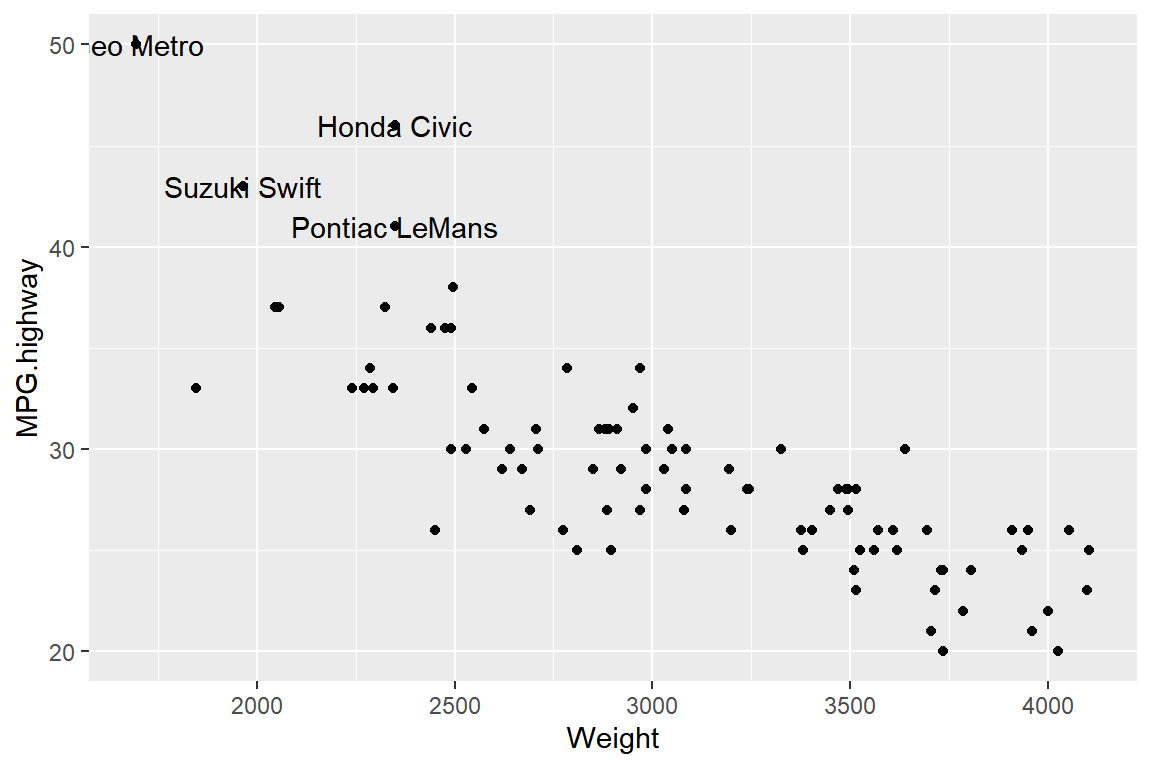
산점도의 점에 라벨 추가

그림 9.74: 산점도의 점에 라벨 추가

추가한 라벨이 점과 겹쳐 있으며, 가장 위에 있는 점의 라벨은 첫 글자가 가려져 있는 것을 볼 수 있다. 라벨의 위치를 조정하는 작업은 vjust와 hjust, nudge_x와 nudge_y로 할 수 있다. 세밀한 조정이 필요한 경우에는 nudge_x와 nudge_y가 더 좋은 방법이 될 수 있다.

p + geom_text(data = filter(Cars93, MPG.highway > 40), 
              aes(label = paste(Manufacturer, Model)),
              nudge_y = 1, nudge_x = 100)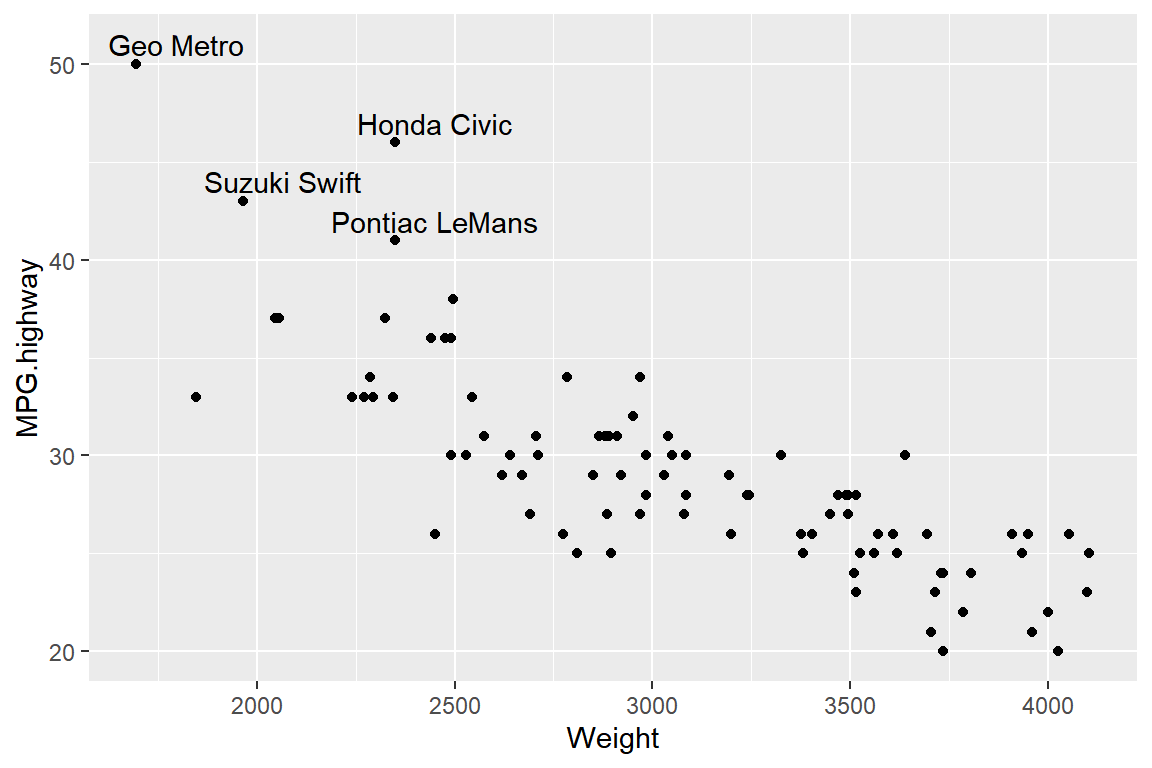
산점도의 점에 라벨 추가 및 위치 조정

그림 9.75: 산점도의 점에 라벨 추가 및 위치 조정

위의 예제는 geom 함수마다 서로 다른 데이터 프레임을 사용할 수 있음을 보여주고 있다. 함수 geom_point()에서는 자료를 모두 사용하여 산점도를 작성했지만, 함수 geom_text()에서는 함수 filter()로 축소된 데이터 프레임을 사용하여 라벨을 붙이는 작업을 진행했다.

\(\bullet\) 산점도에 주석 추가

산점도의 점에 대한 라벨이 아닌 그래프 자체에 주석을 추가하는 것도 함수 geom_text()로 할 수 있다. 만일 R의 수학기호 표현식을 사용하여 주석을 달고 싶다면 옵션 parse = TRUE를 추가해야 한다. 변수 Weight와 MPG.highway의 산점도에 회귀직선을 그리고, 결정계수를 주석으로 추가해 보자. 결정계수는 함수 lm()으로 생성된 객체를 다시 함수 summary()에 입력하여 생성된 객체 중 이름이 r.squared인 객체에 입력되어 있다. 반올림한 결과가 객체 r2에 입력되었다.

fit <- lm(MPG.highway ~ Weight, Cars93) |>
  summary()
r2 <- fit$r.squared |>
  round(2)

그래프 작성 및 주석의 추가는 다음과 같이 할 수 있다.

ggplot(Cars93, aes(x = Weight, y = MPG.highway)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  geom_text(x = 3500, y = 45, size = 7,
            label = paste("R^2==", r2), parse = TRUE)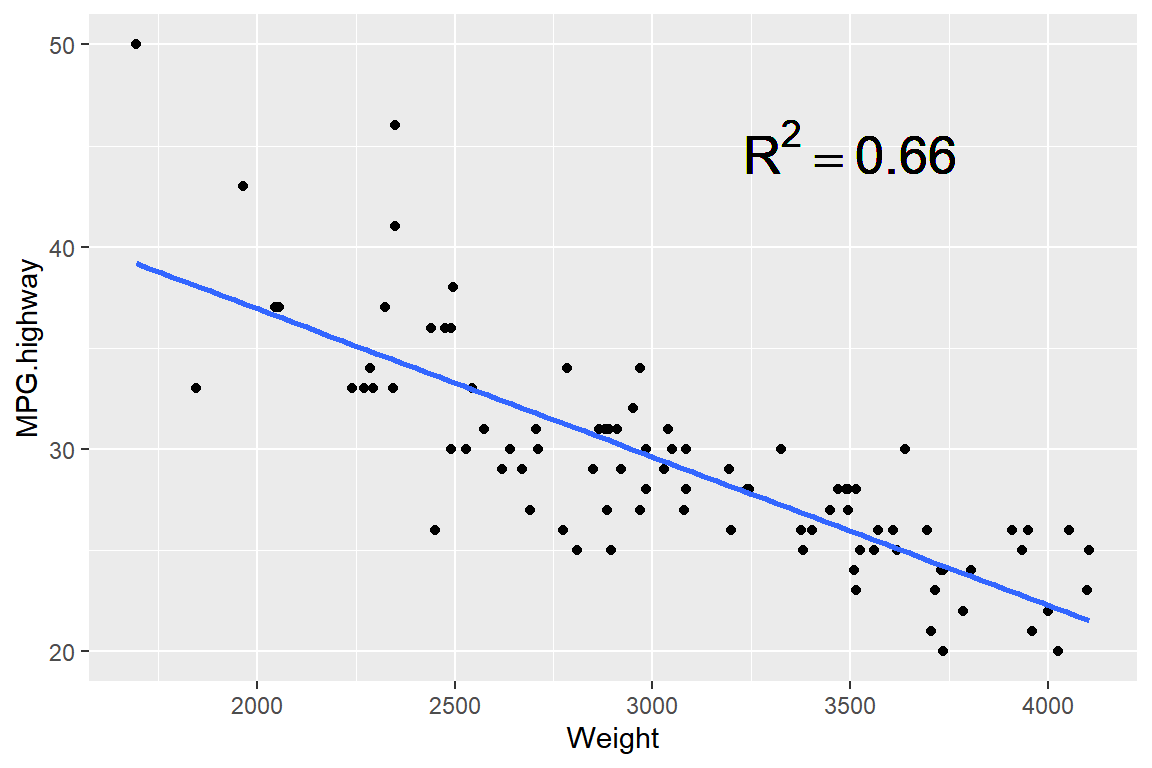
산점도에 수학기호 주석 추가

그림 9.76: 산점도에 수학기호 주석 추가

2) 산점도에서 점이 겹쳐지는 문제

산점도의 점들이 서로 겹쳐지면 자료의 분포나 관계 등을 확인하는 것이 어렵게 된다. 대규모의 자료를 대상으로 산점도를 작성하는 경우 종종 일어나는 현상이며, 두 변수 중 한 변수가 이산형인 경우에도 흔히 볼 수 있는 현상이다. 원자료를 반올림하여 정수로 만들었다면 이산형 자료가 아니어도 겹치는 현상이 발생할 수 있다. 점이 겹쳐지는 문제의 해결 방안은 상황에 따라 달라질 수 밖에 없으며, 마땅한 해결 방안이 없는 상황도 있을 수 있다.

데이터 프레임 ChickWeight는 578마리의 병아리를 대상으로 측정한 몸무게(weight)와 몸무게 측정이 생후 며칠에 이루어졌는지(Time)를 조사한 자료이다. 두 변수의 산점도를 작성해 보자.

ChickWeight |> 
    ggplot(aes(x = Time, y = weight)) +
    geom_point()
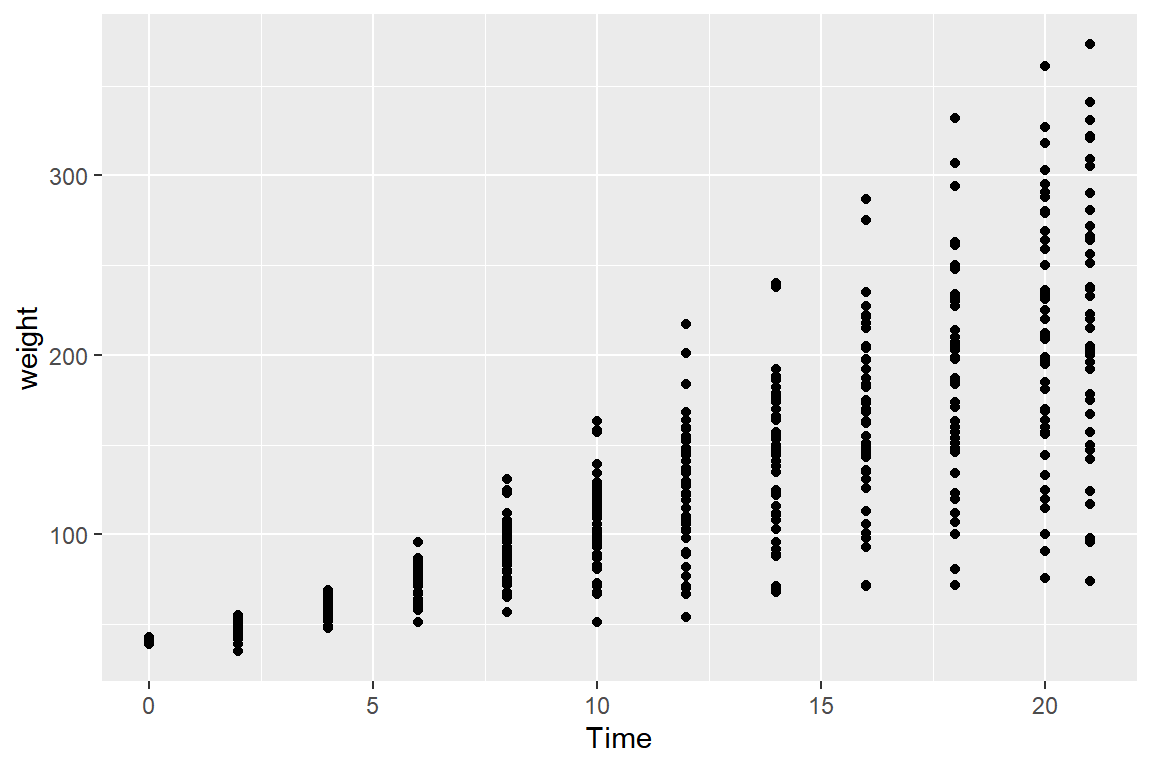
산점도의 점 겹치는 문제

그림 9.77: 산점도의 점 겹치는 문제

변수 Time은 12개의 값만을 갖고 있는 변수이기 때문에 많은 점들이 겹치게 될 수밖에 없다. 이런 경우에는 함수 geom_jitter()을 사용하여 점을 약간 흩트리면 점이 겹치는 정도를 약간 완화할 수 있다.

다른 방법으로 변수 Time이 이산형 변수의 특성을 지니고 있기 때문에 나란히 서 있는 상자그림을 산점도 대신 작성하는 것도 두 변수의 관계 탐색에 도움이 될 수 있다. 함수 geom_boxplot()으로 그룹별 상자그림을 작성할 때 그룹 변수는 반드시 요인 또는 문자형 변수가 되어야 한다. 따라서 숫자형 변수인 Time을 요인으로 전환하여 그룹변수로 매핑하였다.

p1 <- ChickWeight |> 
    ggplot(aes(x = Time, y = weight)) +
    geom_jitter(width = 0.2, height = 0)
p2 <- ChickWeight |> 
    ggplot(aes(x = as.factor(Time), y = weight)) +
    geom_boxplot() + xlab("Time")
p1 + p2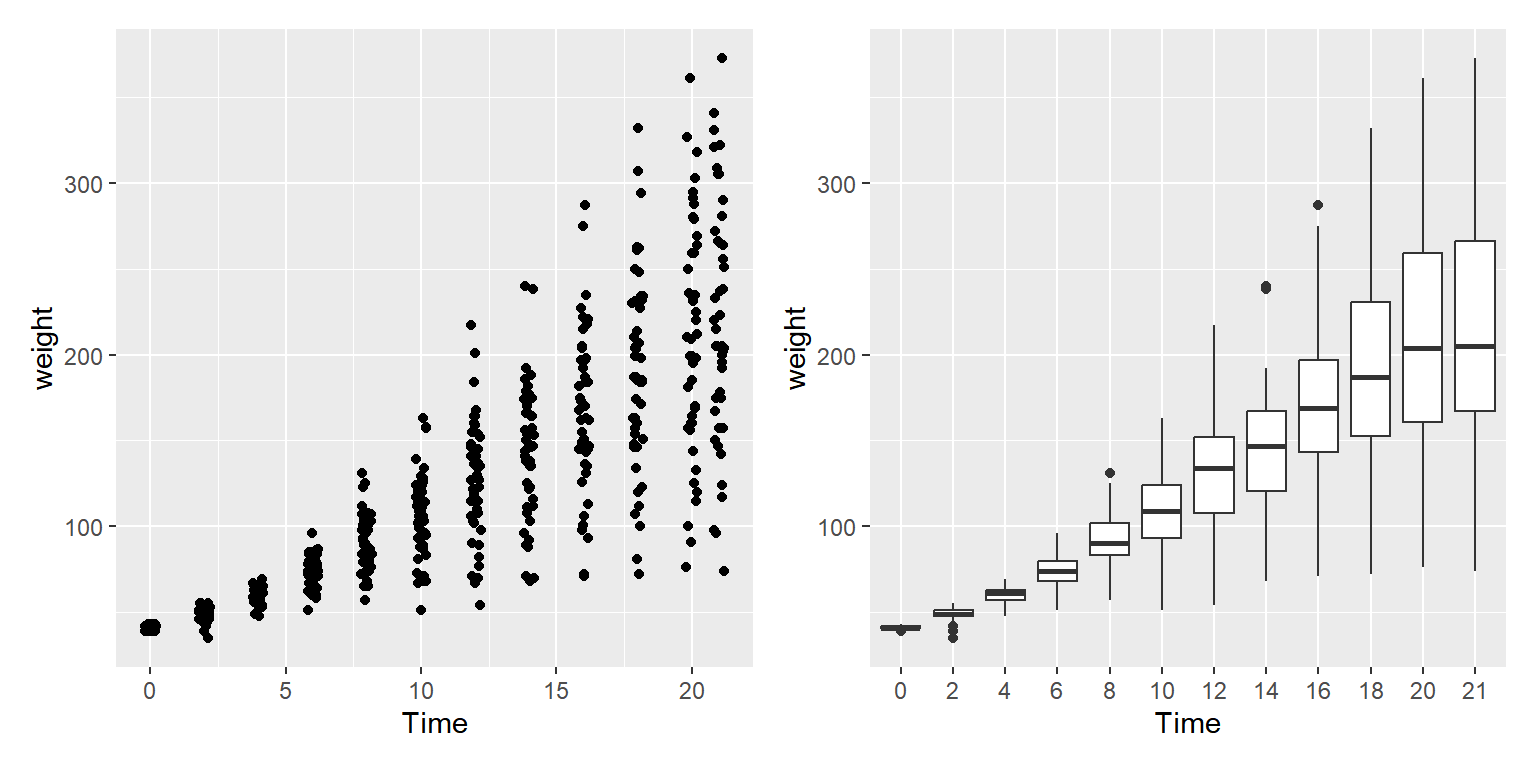
산점도 점 겹치는 문제 해결 방안: 점 흩트리기

그림 9.78: 산점도 점 겹치는 문제 해결 방안: 점 흩트리기

이번에는 대규모 자료를 대상으로 작성된 산점도에서 발생하는 점이 겹쳐지는 현상을 살펴보자. 패키지 ggplot2의 데이터 프레임 diamonds는 53,940개 다이아몬드를 대상으로 가격(price), 무게(carat), 컷의 등급(cut), 색상(color), 투명도(clarity) 등을 조사한 자료이다. 변수 carat과 price의 산점도를 작성해 보자.

ggplot(diamonds, aes(x = carat, y = price)) +
  geom_point()
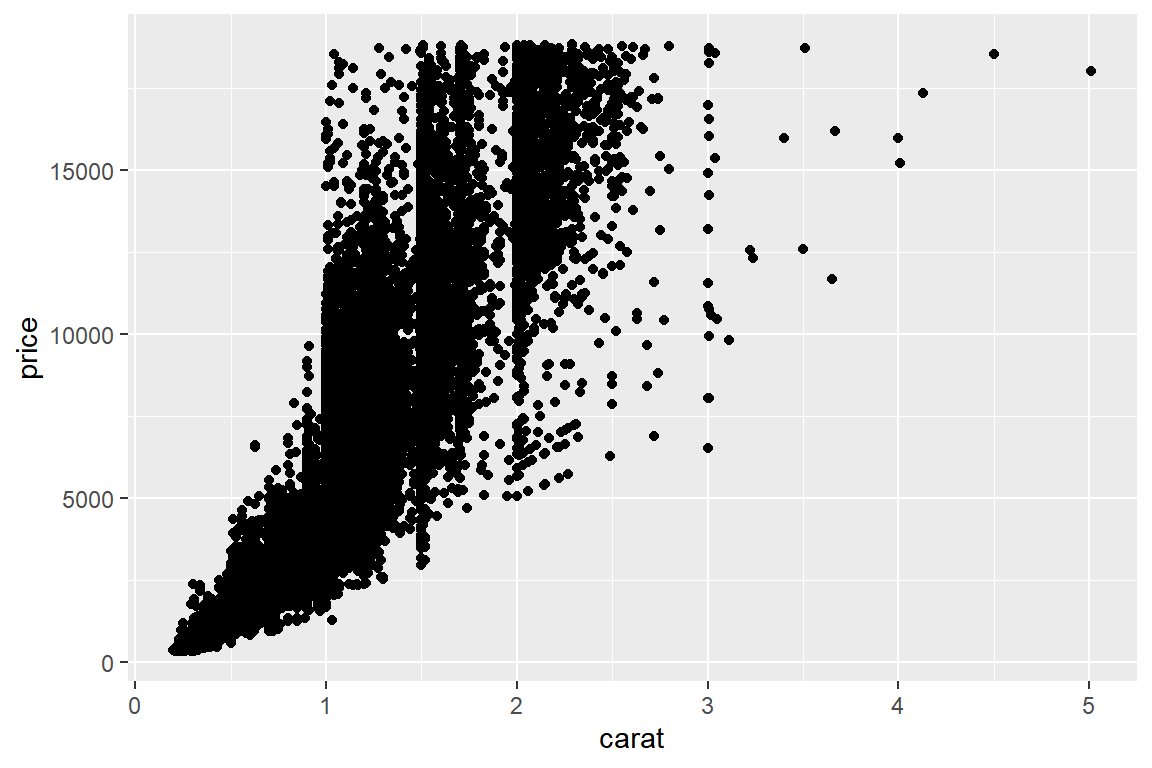
대규모 자료의 산점도에서 점 겹치는 문제

그림 9.79: 대규모 자료의 산점도에서 점 겹치는 문제

점들이 너무 심하게 겹쳐져서 자료의 분포를 알아보기 어려운 상황이다. 변수 carat이 3을 초과하는 자료가 많지 않으므로, carat < 3인 자료만을 대상으로 산점도를 작성해 보자.

p2 <- filter(diamonds, carat < 3) |> 
  ggplot(aes(x = carat, y = price))
p2 + geom_point()
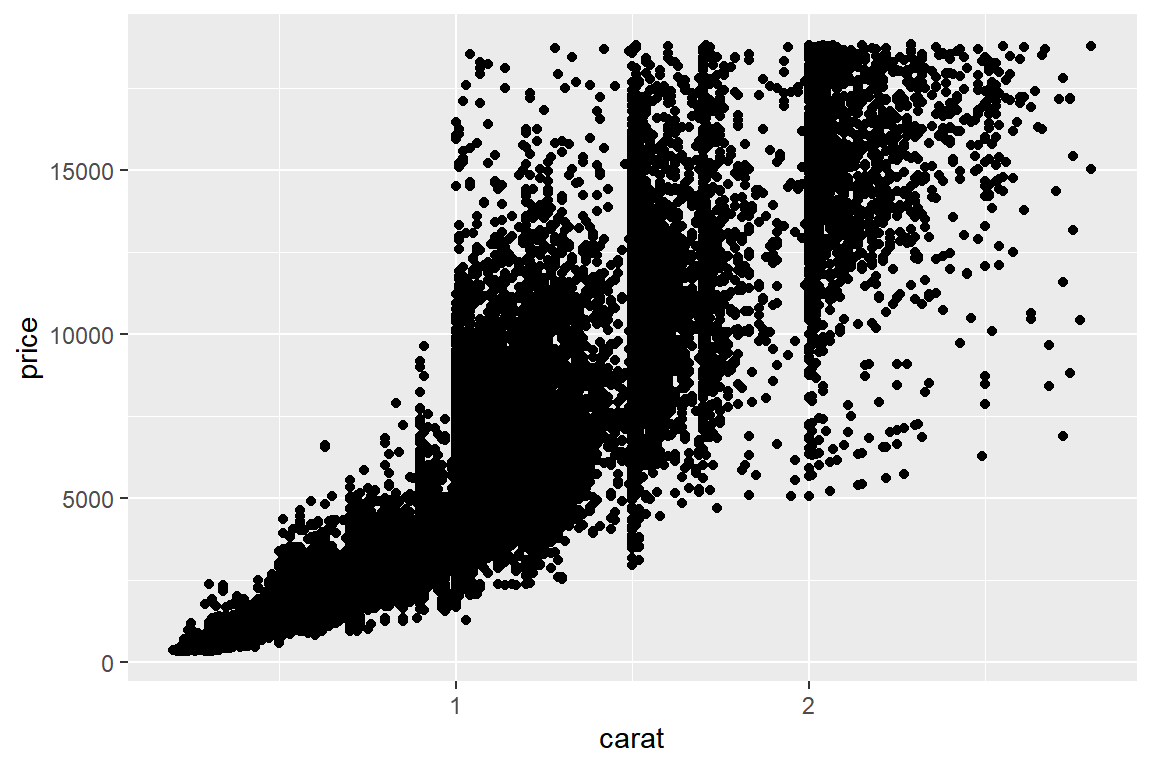
대규모 자료의 산점도에서 점 겹치는 문제

그림 9.80: 대규모 자료의 산점도에서 점 겹치는 문제

대규모 자료를 대상으로 작성된 산점도에서 흔히 발생할 수 있는 문제라고 할 수 있다. 자료의 분포를 확인할 수 있는 첫 번째 방법으로 점의 크기를 줄이고 투명도를 높이는 것을 생각해 볼 수 있다. 함수 geom_point()에서 점 모양은 shape = 16이 디폴트인데, shape = 20을 사용하면 점의 크기가 조금 줄어든다. alpha를 0에 가까운 값을 지정하면 투명도를 높일 수 있다.

p2 + geom_point(alpha = 0.1, shape = 20)
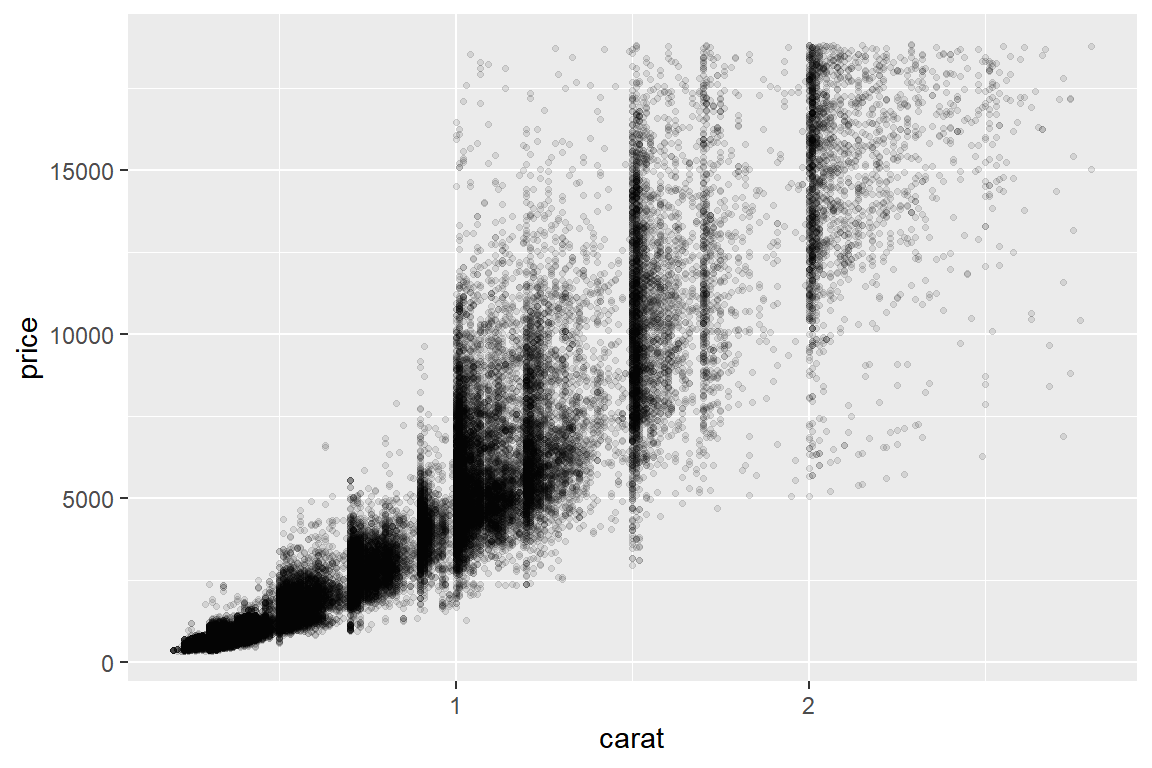
대규모 자료의 산점도에서 점 겹치는 문제 해결 방안: 점의 크기 줄이고 투명도 높이기

그림 9.81: 대규모 자료의 산점도에서 점 겹치는 문제 해결 방안: 점의 크기 줄이고 투명도 높이기

점의 크기를 줄이고 투명도를 높이는 것으로는 문제가 해결되지 않는 것으로 보인다. 다만, 특정 carat의 값에서 점들이 수직의 띠를 형성하는 것이 보인다. 이것은 carat의 값이 같더라도 price에는 큰 차이가 있다는 것이며, 따라서 price의 변동을 설명하기 위해서는 다른 변수가 더 있어야 한다는 것을 보이는 것이다.

두 번째 방법으로는 함수 geom_bin2d()로 2차원 히스토그램을 작성하는 것이다. 이것은 XY축으로 형성된 2차원 공간을 직사각형의 영역(2D bin)으로 나누고, 각 영역에 속한 자료의 개수를 색으로 나타내는 그래프를 작성하는 것이다. 히스토그램을 2차원으로 확장한 그래프라고 할 수 있다. X축과 Y축을 30개의 구간으로 나누어 전체 공간을 900개의 직사각형으로 나누는 것이 디폴트이다.

p2 + geom_bin2d()
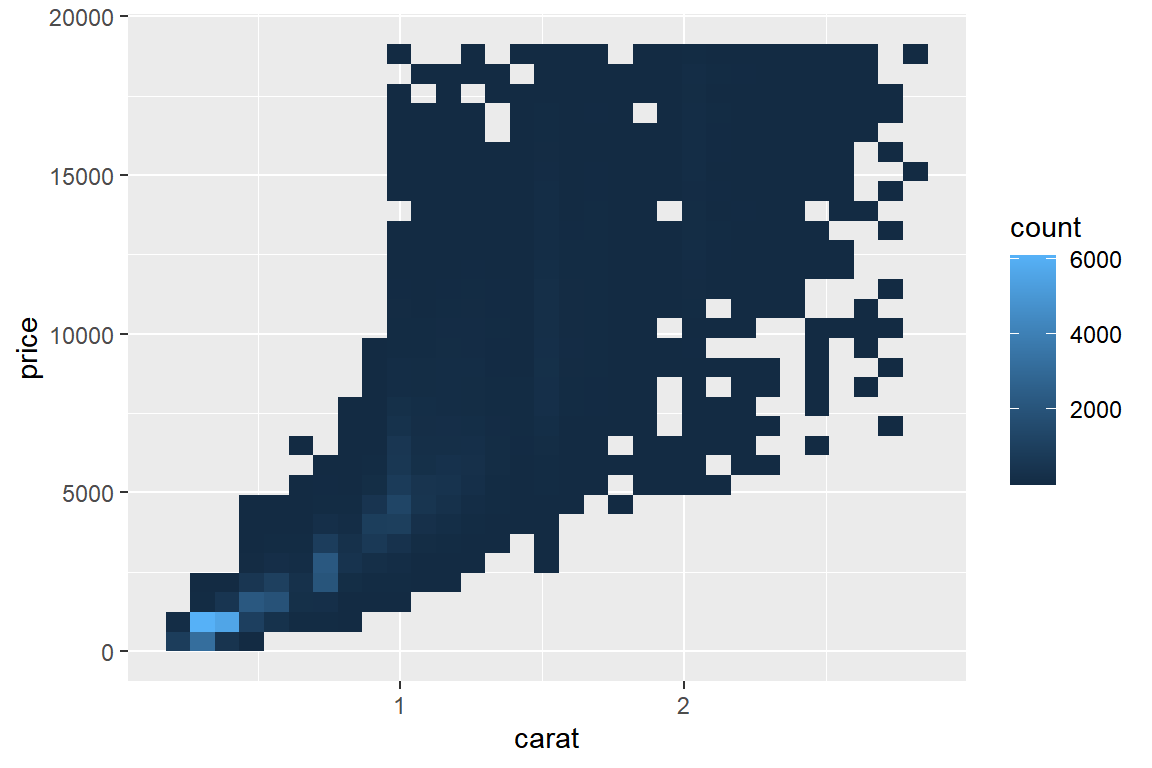
대규모 자료의 산점도에서 점 겹치는 문제 해결 방안: 2차원 히스토그램

그림 9.82: 대규모 자료의 산점도에서 점 겹치는 문제 해결 방안: 2차원 히스토그램

빈도수를 나타내는 색깔에 큰 변화가 없어서 구분이 잘 안 되고 있고, 구간의 개수를 더 늘릴 필요가 있는 것으로 보인다. 디폴트 구간 개수인 30개를 원하는 개수로 조정하는 옵션은 bins이다. 색깔의 조정은 함수 scale_fill_gradient()에서 원하는 색깔을 low와 high에 각각 지정하면 된다. 대부분의 다이아몬드가 작고 가격이 상대적으로 싼 편이라는 것을 알 수 있다.

p2 + geom_bin2d(bins = 100) +
  scale_fill_gradient(low = "skyblue", high = "red")
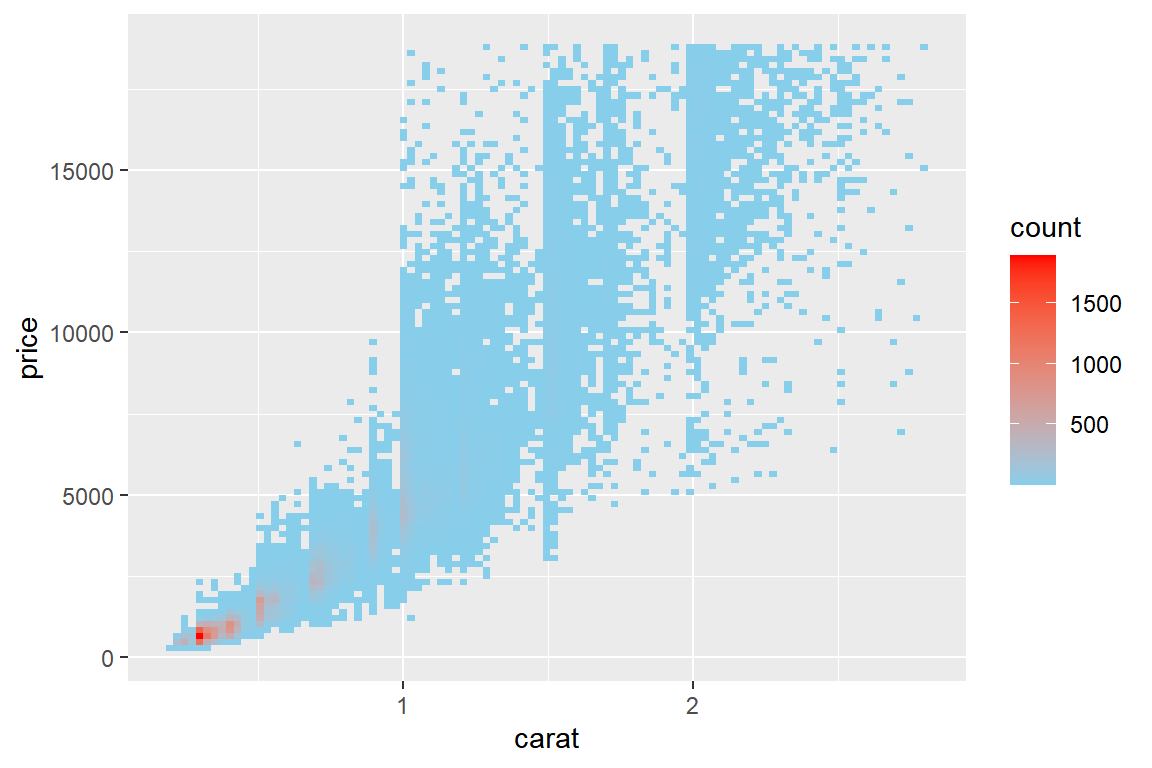
대규모 자료의 산점도에서 점 겹치는 문제 해결 방안: 2차원 히스토그램

그림 9.83: 대규모 자료의 산점도에서 점 겹치는 문제 해결 방안: 2차원 히스토그램

세 번째 방법은 X축 변수인 carat이 이산형 변수가 아니지만, 이것을 구간으로 구분하여 나란히 서 있는 상자그림을 작성하는 것이다. 숫자형 변수를 구간으로 구분하는 데 유용한 함수가 cut_width()와 cut_number(), cut_interval()이다. 구간의 간격을 동일하게 한다면 cut_width(x,width, boundary)를 사용하면 된다. 옵션 boundary는 구간의 시작점을 지정할 때 사용한다. 반면에 자료를 n개 구간으로 구분하되, 각 구간에 속한 자료의 개수를 동일하게 한다면 cut_number(x, n)을 사용하면 되고, 간격이 length인 n개 그룹으로 구분한다면 cut_interval(x, n, length)를 사용하면 된다. 이 함수들을 실행시키면 각 구간을 수준으로 갖는 요인이 생성된다.

변수 carat을 0을 시작점으로 0.1의 간격을 갖는 구간으로 구분하고, 각 구간의 자료들을 대상으로 상자그림을 작성해 보자. 또한 변수 carat을 20개 구간으로 구분하되 각 구간에 속한 자료의 개수를 가능한 동일하도록 하고 상자그림을 작성해 보자.

bp1 <- p2 + geom_boxplot(aes(group = cut_width(carat, width = 0.1, boundary = 0)))
bp2 <- p2 + geom_boxplot(aes(group = cut_number(carat, n = 20)))
bp1 + bp2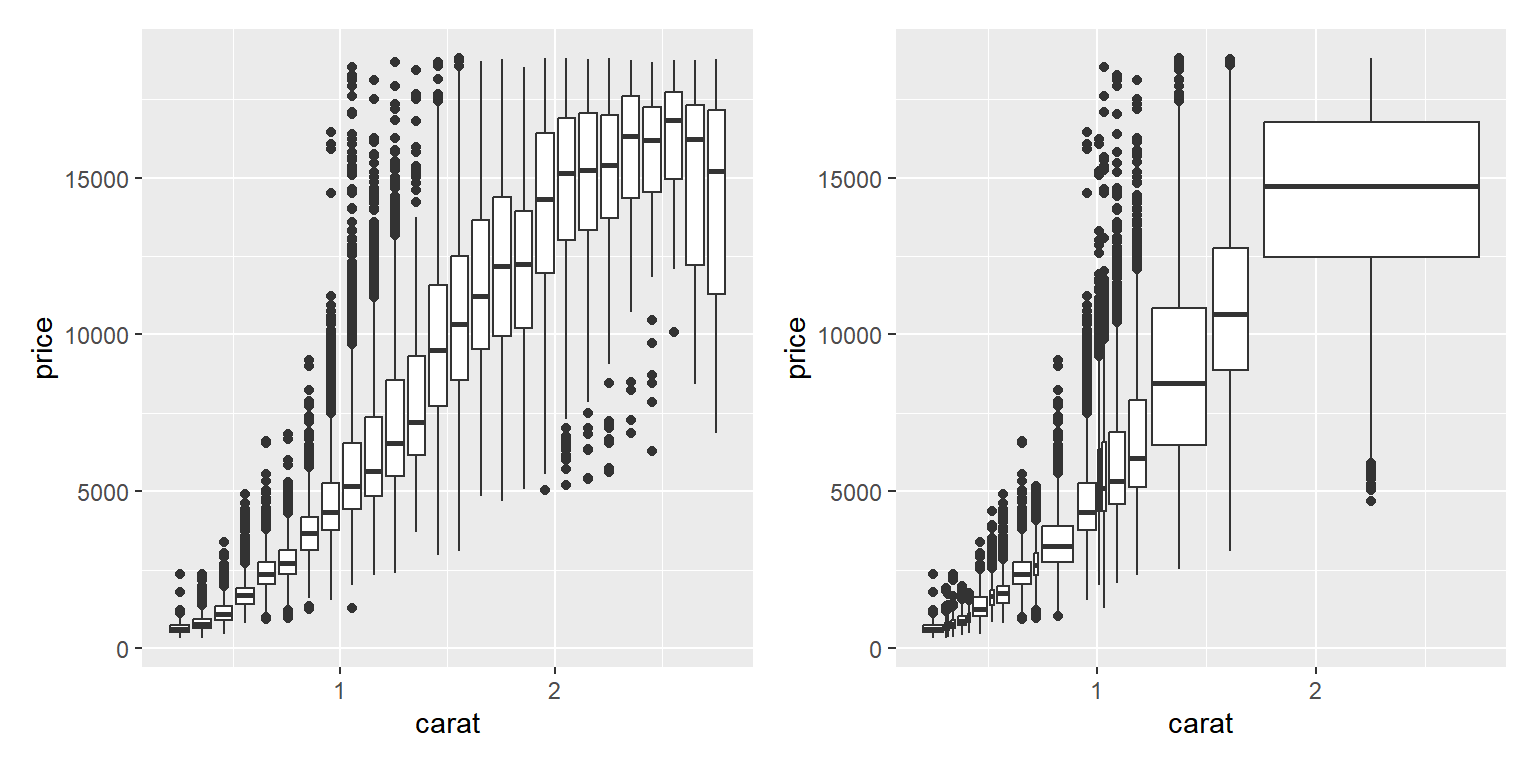
대규모 자료의 산점도에서 점 겹치는 문제 해결 방안: 그룹별 상자그림

그림 9.84: 대규모 자료의 산점도에서 점 겹치는 문제 해결 방안: 그룹별 상자그림

3) 이차원 결합확률밀도 그래프

두 연속형 변수의 관계를 탐색할 때 두 변수의 결합확률밀도를 추정한 그래프가 큰 역할을 할 수 있다. 데이터 프레임 faithful의 두 변수 eruptions와 waiting의 결합확률밀도를 추정하여 그래프로 작성해 보자. 기본적인 그래프는 함수 geom_density_2d()로 작성할 수 있는데, 등고선 그래프가 작성된다.

p3 <- ggplot(faithful, aes(x = eruptions, y = waiting)) +
  xlim(1, 6) + ylim(35, 100)
p3 + geom_density2d()
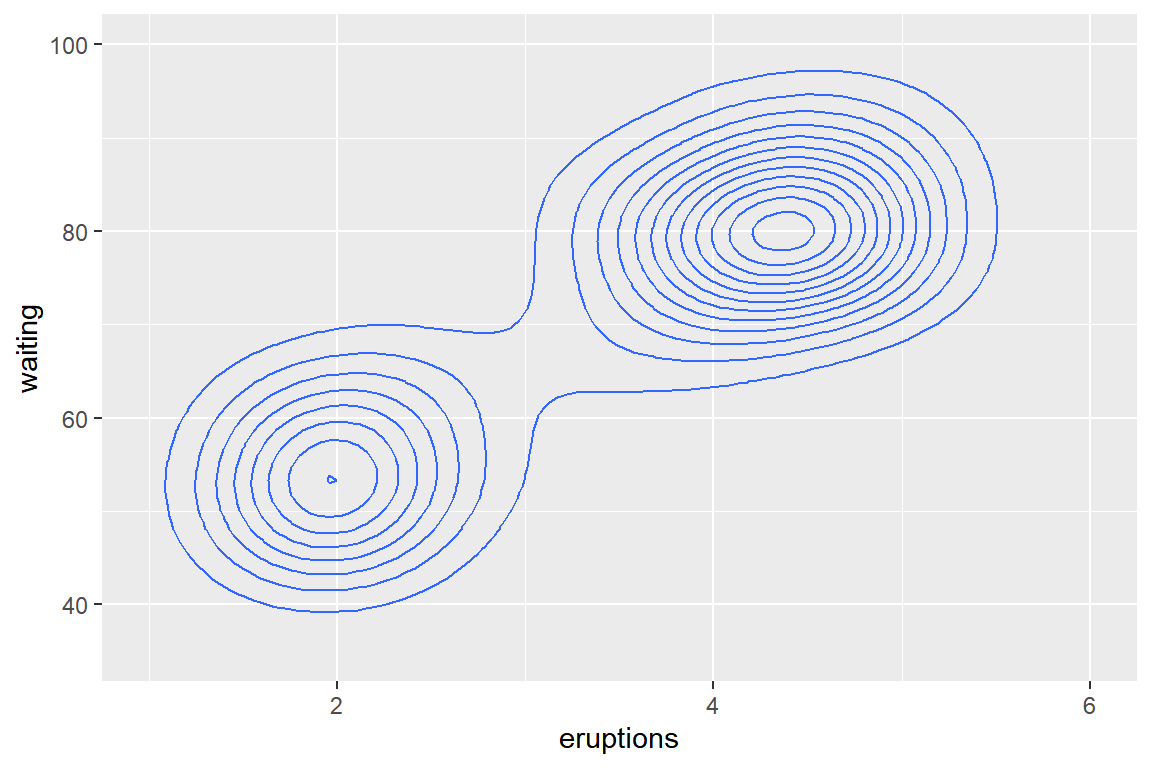
결합확률밀도 등고선 그래프

그림 9.85: 결합확률밀도 등고선 그래프

등고선 그래프는 3차원 자료를 2차원 공간에 표시한 것으로 확률밀도가 같은 영역을 선으로 연결하여 그린 그래프다. 각 등고선에 적절한 라벨이 붙어 있어야 확률밀도가 높은 지역과 낮은 지역을 구분할 수 있지만, 라벨을 일일이 확인하여 높이를 구분하는 작업은 매우 번거롭고 부정확할 수밖에 없다. 대안으로 제시되는 방법은 등고선의 높이를 색으로 구분하는 것이다. 시각적 요소 color를 함수 stat_density_2d()에서 계산된 변수 after_stat(level)에 매핑하여 선의 색깔을 구분시켜 보자. 함수 scale_color_gradient()를 사용하여 색깔의 변화를 조정하였다. 두 변수의 산점도를 함께 작성하는 것도 좋을 것이다.

bp1 <- p3 + geom_density_2d(aes(color = after_stat(level))) +
    scale_color_gradient(low = "blue", high = "red")
bp2 <- bp1 + geom_point(shape = 20)
bp1 + bp2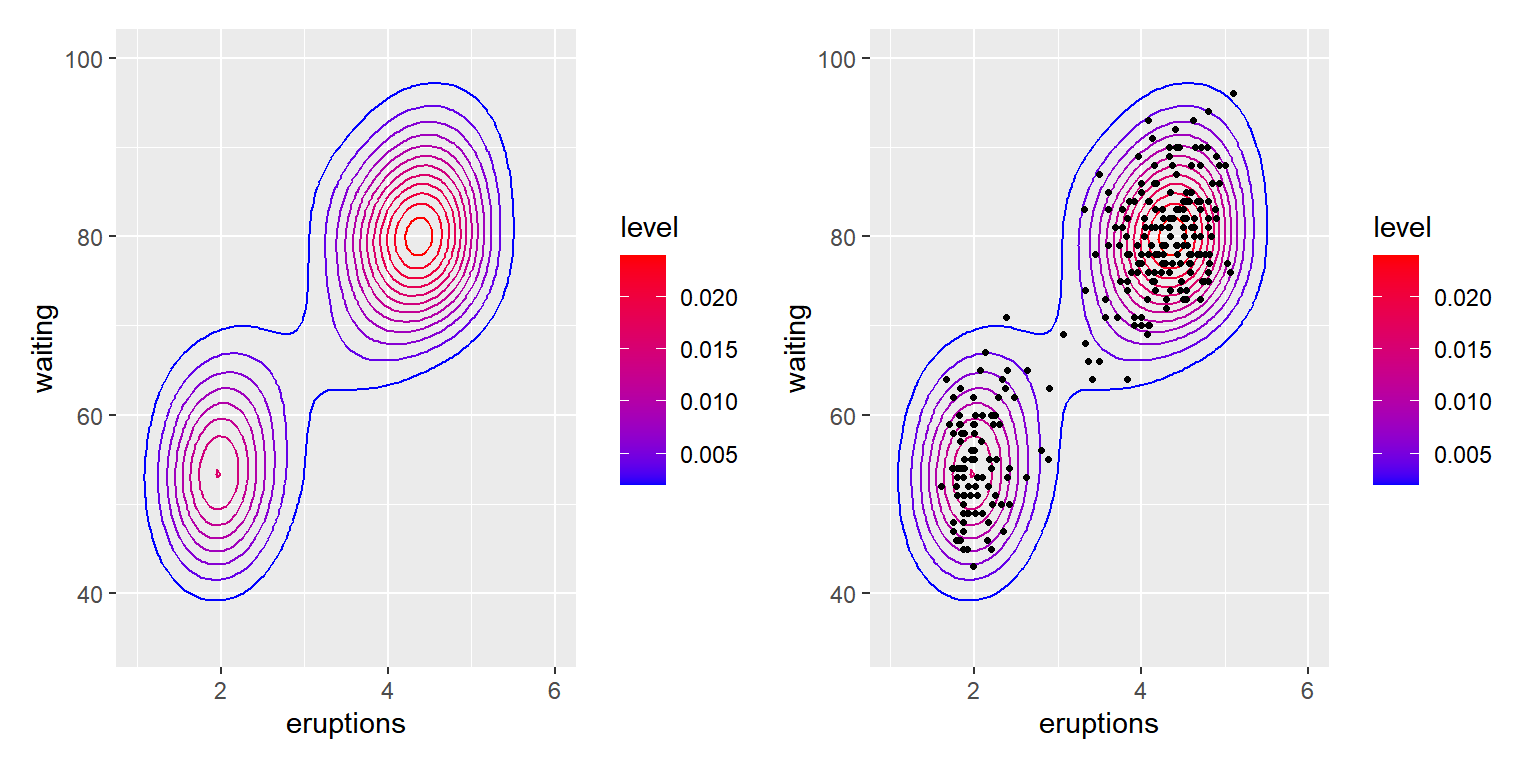
결합확률밀도 등고선 그래프

그림 9.86: 결합확률밀도 등고선 그래프

등고선만을 색으로 구분하는 것보다는 높이가 같은 영역을 구분된 색으로 채우는 것이 더 효율적인 그래프가 될 것이다. 작성 방법은 함수 stat_density_2d()를 사용하여 geom에 "polygon"을 지정하고, 시각적 요소 fill에 after_stat(level)을 매핑하는 것이다.

p3 + stat_density_2d(aes(fill = after_stat(level)), geom = "polygon")
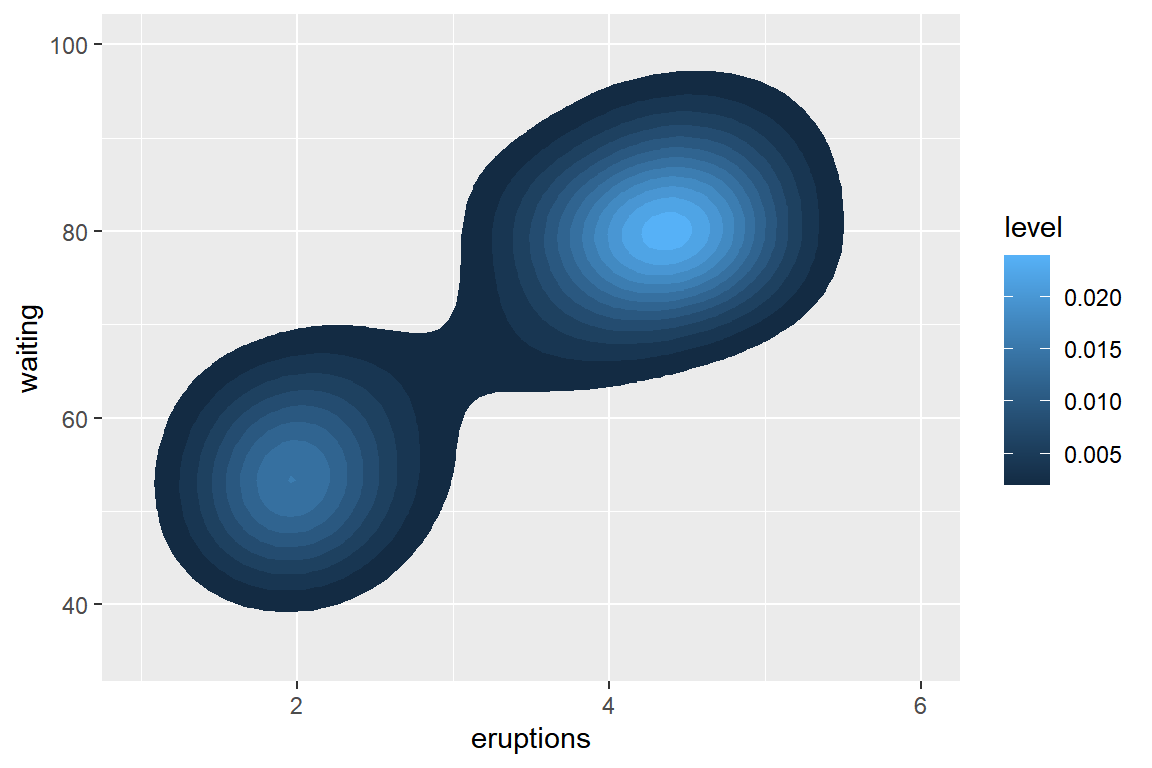
색을 이용한 결합확률밀도 그래프

그림 9.87: 색을 이용한 결합확률밀도 그래프

등고선내부 영역만을 색으로 채우기보다 그래프 전체 영역을 타일로 구분하고, 확률밀도의 높이에 따라 타일의 색을 다르게 하는 것이 훨씬 안정적인 느낌의 그래프를 작성하는 방법이 된다. 직사각형의 타일을 만드는 작업은 함수 geom_tile() 또는 geom_raster()를 사용해야 하는데, 두 변수에 대한 반응표면을 작성하는 경우에는 함수 geom_raster()를 사용하는 것이 좋다. 두 변수의 결합확률밀도 그래프도 일종의 반응표면을 작성하는 것이므로 geom_raster()를 사용해 보자. 타일의 색을 구분하기 위한 결합확률밀도의 추정 결과는 함수 stat_density_2d()에서 after_stat(density)에 입력되어 있으며, 이것을 시각적 요소 fill에 매핑하면 된다. 이때 옵션 contour은 반드시 FALSE로 지정해야 한다.

p3 + stat_density_2d(aes(fill = after_stat(density)),geom = "raster", 
                     contour = FALSE) +
  scale_fill_gradient(low = "skyblue", high = "red")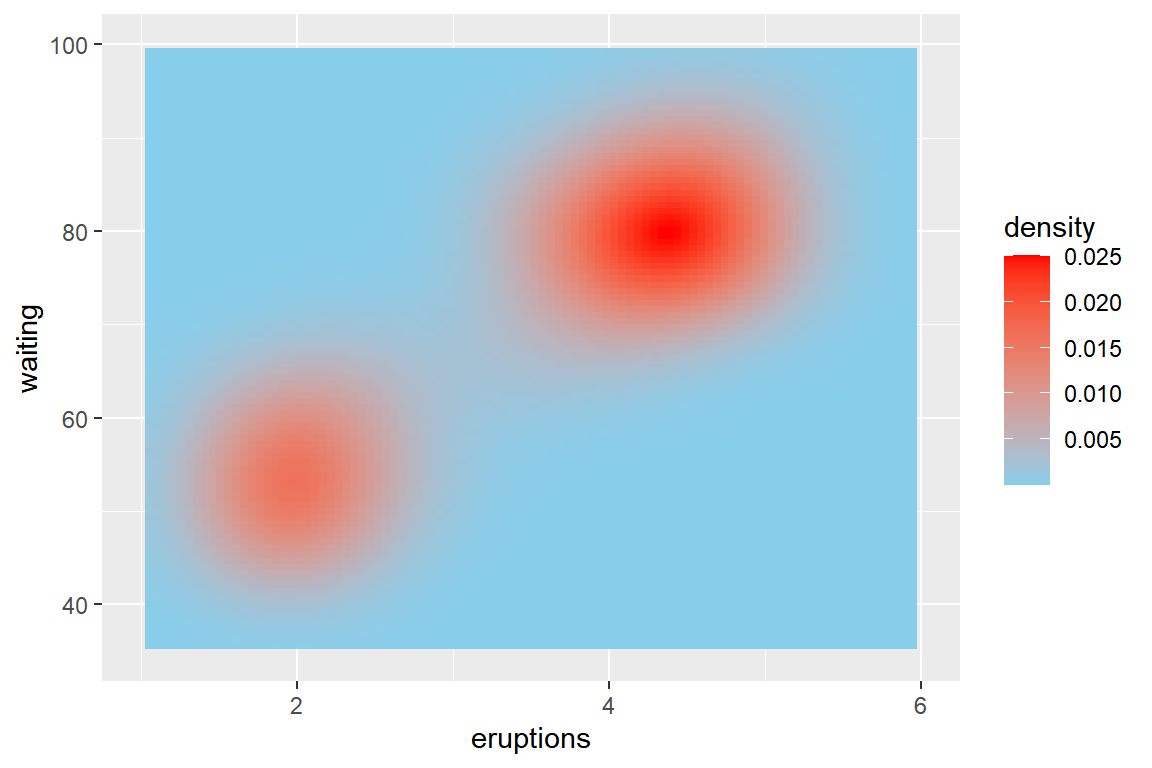
색을 이용한 결합확률밀도 그래프

그림 9.88: 색을 이용한 결합확률밀도 그래프

패키지 ggplot2에는 데이터 프레임 faithful의 두 변수인 eruptions와 waiting의 결합확률밀도 추정 결과가 변수(density)로 포함된 데이터 프레임 faithfuld가 있다. 변수 density에 할당된 결합확률밀도의 추정은 XY축에 75개의 격자점을 각각 구성하여 형성된 75×75=5625의 점에서 이루어졌다. 이와 같이 결합확률밀도의 높이가 데이터 프레임의 변수로 주어진 경우에는 함수 geom_raster()로 간단하게 그래프를 작성할 수 있다. 다만 이 경우에는 옵션 interpolate에 TRUE를 지정하는 것이 훨씬 안정적인 그래프를 작성하는 방법이다.

ggplot(faithfuld, aes(x = eruptions, y = waiting)) +
  geom_raster(aes(fill = density), interpolate = TRUE) +
  scale_fill_gradient(low = "skyblue", high = "red")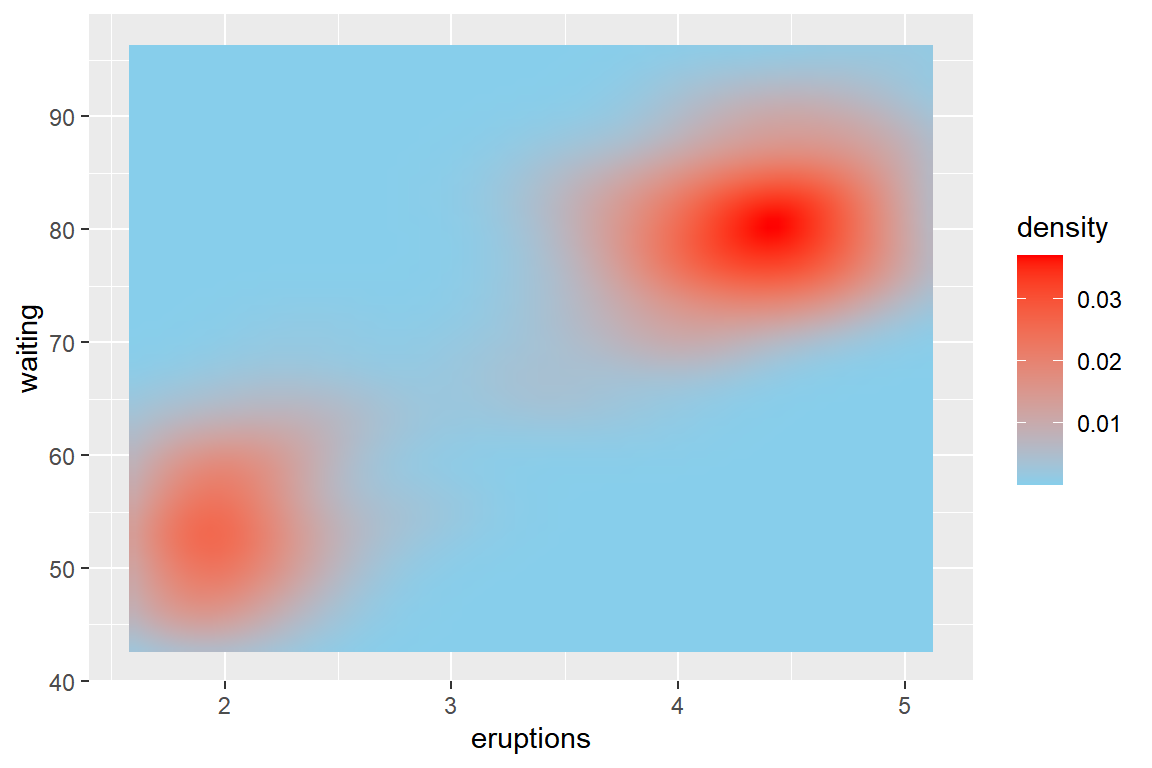
결합확률밀도 그래프

그림 9.89: 결합확률밀도 그래프

4) 산점도행렬(scatter plot matrix)

산점도행렬은 여러 변수로 이루어진 자료에서 두 변수끼리 짝을 지어 작성된 산점도를 행렬의 행태로 배열하여 하나의 그래프로 함께 나타낸 그래프이다. 복잡하고 어려운 문제를 간단하고 명확하게 해결할 수 있도록 도와주는 뛰어난 그래프라고 할 수 있다. 패키지 ggplot2에는 산점도행렬을 작성하는 함수가 없지만, 패키지 GGally의 함수 ggpairs()로 작성할 수 있다. 패키지 GGally는 ggplot2의 확장이라고 할 수 있는데, 산점도행렬, 평행좌표 그래프, 생존 그래프와 네트워크를 나타내는 그래프, 모형 검진을 위한 그래프 등등 유용한 그래프를 작성할 수 있다.

예제로 데이터 프레임 mtcars에서 변수 mpg, wt, disp, cyl, am의 산점도행렬을 작성해 보자. 함수 ggpairs()에는 산점도행렬 작성에 사용될 변수만으로 이루어진 데이터 프레임을 입력하는 것이 좋다.

mtcars_1 <- mtcars |>
  select(mpg, wt, disp, cyl, am)
library(GGally)
ggpairs(mtcars_1)
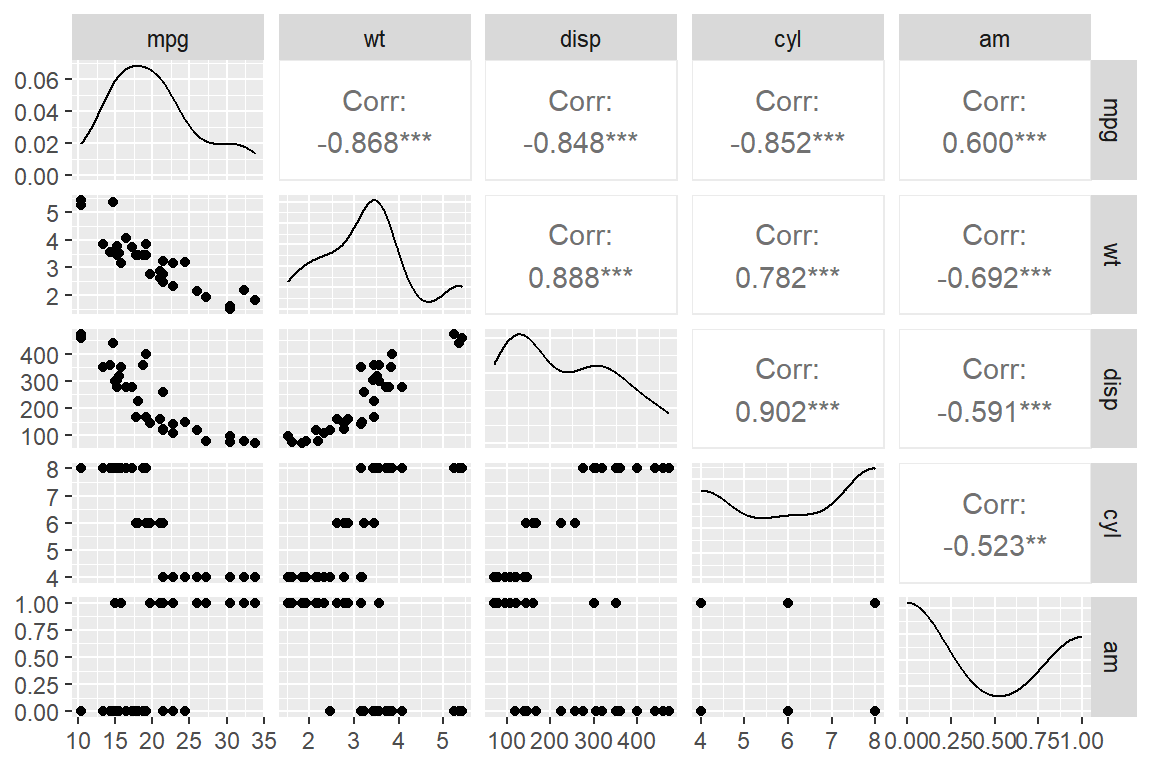
숫자형 변수에 대한 함수 `ggpairs()`의 산점도행렬

그림 9.90: 숫자형 변수에 대한 함수 ggpairs()의 산점도행렬

데이터 프레임 mtcars의 모든 변수는 숫자형 변수로 선언되어 있다. 변수 am과 cyl을 요인으로 전환시키고 다시 산점도행렬을 작성해 보자.

mtcars_2 <- mtcars_1 |>
  mutate(am = factor(am), cyl = factor(cyl))
ggpairs(mtcars_2)
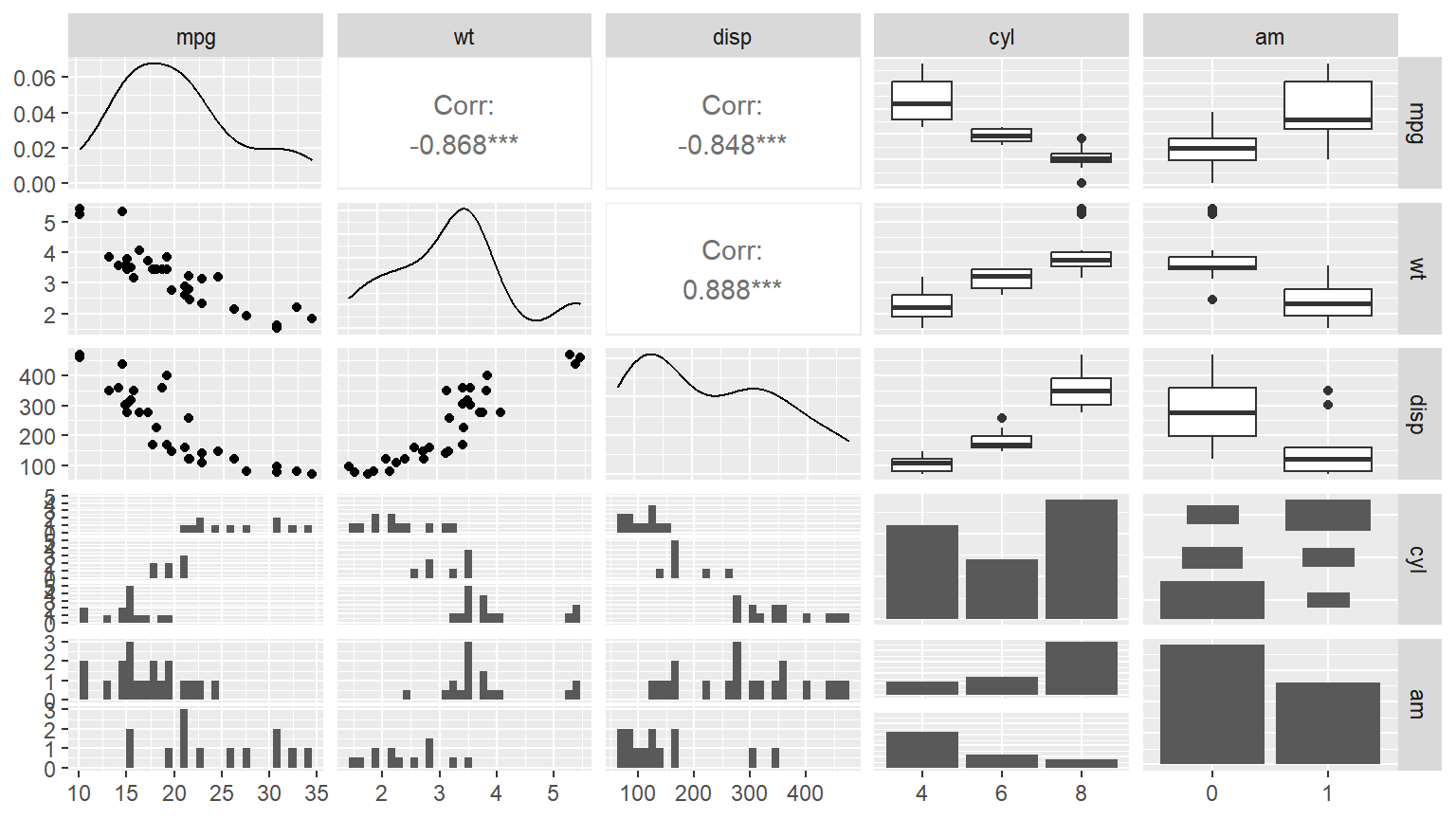
숫자형 변수와 요인이 있는 자료에 대한 함수 `ggpairs()`의 산점도행렬

그림 9.91: 숫자형 변수와 요인이 있는 자료에 대한 함수 ggpairs()의 산점도행렬

함수 ggpairs()로 작성된 산점도행렬은 단순히 두 변수의 산점도만을 작성하는 것이 아니라 변수의 유형에 따라 적절한 형태의 그래프를 각 패널에 작성한다. 변수의 유형은 두 변수가 모두 양적 변수 또는 질적 변수인 경우와 두 유형이 섞여 있는 경우로 구분된다. 또한 패널의 위치가 대각선인지, 혹은 대각선 위쪽인지, 혹은 대각선 아래쪽인지에 따라 다른 유형의 그래프가 작성되는 것이 디폴트이다.

각 패널에 작성되는 디폴트 그래프를 살펴보자. 대각선 패널의 경우, 양적변수는 확률밀도그래프가 작성되고 질적 변수는 막대그래프가 작성된다. 대각선 위쪽 패널의 경우, 두 변수가 모두 양적 변수이면 상관계수가 계산되고, 하나는 양적 변수, 다른 하나는 질적 변수이면 상자그림이 작성되며, 둘다 질적 변수이면 facet 막대그래프가 작성된다. 대각선 아래쪽 패널의 경우, 둘 다 양적 변수이면 산점도, 둘 다 질적 변수이면 facet 막대그래프, 섞여 있으면 facet 히스토그램이 각각 작성된다.

각 패널에 작성되는 그래프를 바꾸는 방법을 살펴보자. 대각선 위 아래 패널의 경우에는 upper 혹은 lower를 이용해야 한다. 두 옵션은 요소 continuous와 combo, discrete로 이루어진 리스트로써 원하는 그래프에 해당하는 키워드를 각 요소에 지정하면 된다. 양적 변수(continuous)에 사용할 수 있는 키워드는 "points", "smooth", "smooth_loess", "density","cor", "blank"가 있고, 질적 변수(discrete)에 사용할 수 있는 키워드는 "facetbar", "ratio", "blank"가 있으며, 섞여 있는 경우(combo)에는 "box", "box_no_facet", "dot", "dot_no_facet", "facethist", "facetdensity", "denstrip", "blank"가 있다.

대각선 패널의 경우에는 옵션 diag에 continuous와 discrete로 이루어진 리스트에 원하는 그래프에 해당하는 키워드를 지정해야 한다. 사용 가능한 키워드로 continuous에는 "densityDiag", "barDiag", "blankDiag"가 있고, discrete에는 "barDiag", "blankDiag"가 있다.

각 그래프를 작성할 때 디폴트로 주어진 변수가 있다. 예를 들어 히스토그램을 작성할 때 구간은 bins = 30으로 설정되는 것이 디폴트이다. 이러한 디폴트 값을 변경하고자 한다면 함수 wrap()을 사용하여 필요한 변수 값을 지정하면 된다.

이제 mtcars_2를 대상으로 다음의 조건으로 수정된 형태의 산점도행렬을 작성하자. 대각선 아래쪽 패널의 continuous에는 "smooth"를 지정해서 회귀직선을 추가하되, se = FALSE를 추가해서 신뢰구간은 제거하고, combo의 경우에는 "facethist"를 지정해서 facet 히스토그램을 작성하되, bins = 10으로 구간의 개수를 10개로 지정하자. 대각선 위쪽 패널의 continuous에는 "density"를 지정해서 결합확률밀도그래프를 작성해 보자. 또한 모든 패널의 그래프를 요인 am에 의한 두 그룹으로 구분해서 작성하는데, 이것은 시각적 요소 color에 요인 am을 매핑하면 된다.

ggpairs(mtcars_2, aes(color = am),
          upper = list(continuous = "density"),
          lower = list(continuous = wrap("smooth", se = FALSE),
                       combo = wrap("facethist", bins = 10)))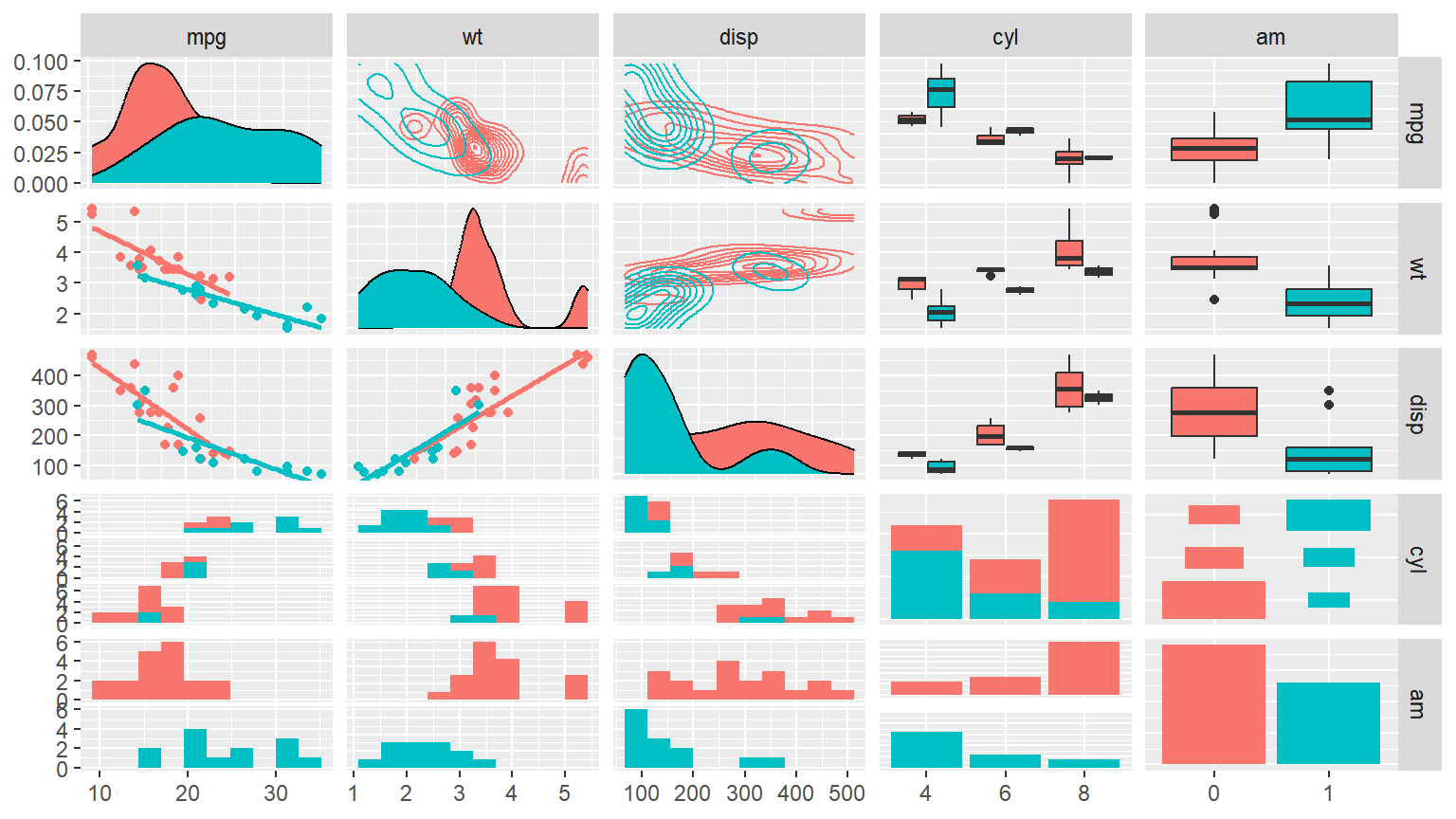
숫자형 변수와 요인이 있는 자료에 대한 함수 `ggpairs()`의 산점도행렬

그림 9.92: 숫자형 변수와 요인이 있는 자료에 대한 함수 ggpairs()의 산점도행렬

9.5 연습문제

1. 패키지 UsingR의 데이터 프레임 normtemp는 화씨 98.6도를 “정상” 체온이라고 할 수 있는지를 확인하기 위해 성인 130명을 대상으로 체온과 심박수를 측정한 자료이다. 변수 temperature는 화씨로 측정된 체온이고, gender는 1(남자), 2(여자)를 값으로 갖고 있으며, hr은 안정 시 측정된 심박수이다.

  • 화씨로 측정된 변수 temperature의 값을 섭씨로 변환시키고, gender는 male과 female을 범주로 갖는 요인으로 변환시키자. 단, 섭씨 온도는 \((\)화씨 온도\(-32) \times \frac{5}{9}\)이다.

  • 주어진 자료에서 체온과 관련된 어떤 정보를 얻을 수 있는가? 필요한 그래프를 작성하고, 그 결과를 설명하라.

2. 패키지 MASS의 데이터 프레임 survey는 학생 237명을 대상으로 조사한 자료이다.

  • 변수 중 요인만을 선택해서 변수 이름을 다음과 같이 벡터 형태로 출력해 보자.
## [1] "Sex"   "W.Hnd" "Fold"  "Clap"  "Exer"  "Smoke" "M.I"
  • 각 요인 변수의 범주 개수를 확인해서 다음과 같이 출력해 보자.
## # A tibble: 1 × 7
##     Sex W.Hnd  Fold  Clap  Exer Smoke   M.I
##   <int> <int> <int> <int> <int> <int> <int>
## 1     2     2     3     3     3     4     2
  • 변수 중 요인만을 선택해서 각 변수의 막대그래프를 다음과 같은 형태로 작성해 보자.

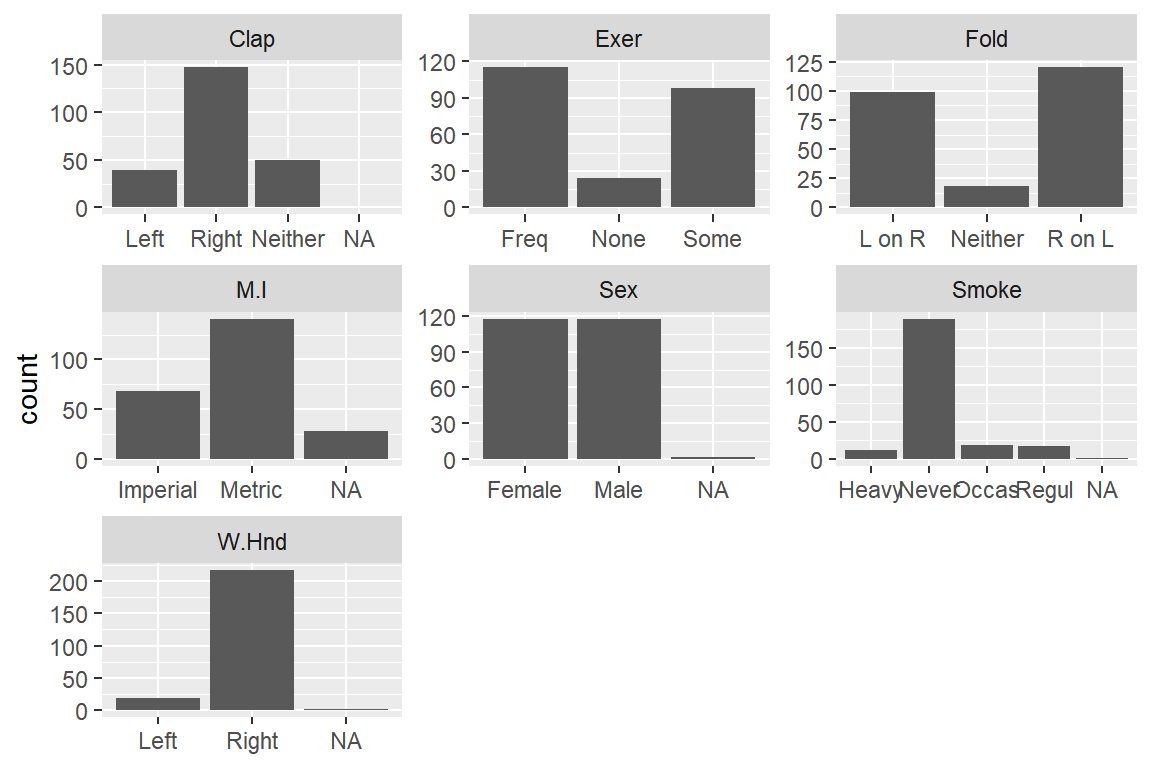
  • 앞 문제에서 작성된 막대그래프에는 NA가 범주로 포함된 변수들이 있다. 각 변수별로 결측값의 개수를 확인해서 다음과 같이 출력해 보자.
## # A tibble: 1 × 7
##     Sex W.Hnd  Fold  Clap  Exer Smoke   M.I
##   <int> <int> <int> <int> <int> <int> <int>
## 1     1     1     0     1     0     1    28
  • 변수 Sex와 Smoke에 결측값이 있는 케이스를 제거하고, 변수 Smoke의 범주 중 Heavy, Occas, Regul는 yes로 통합하며, Never는 no로 변경시켜서 새로운 데이터 프레임 survey_S에 할당하자. 변경된 데이터 프레임에서 변수 Smoke의 도수분포를 구해서 다음과 같이 출력해 보자.
## # A tibble: 2 × 2
##   Smoke     n
##   <fct> <int>
## 1 yes      47
## 2 no      188
  • 데이터 프레임 survey_S를 사용해서 변수 Sex와 Smoke의 다음과 같은 이변량 막대그래프를 작성하고, 의미를 해석해 보자.

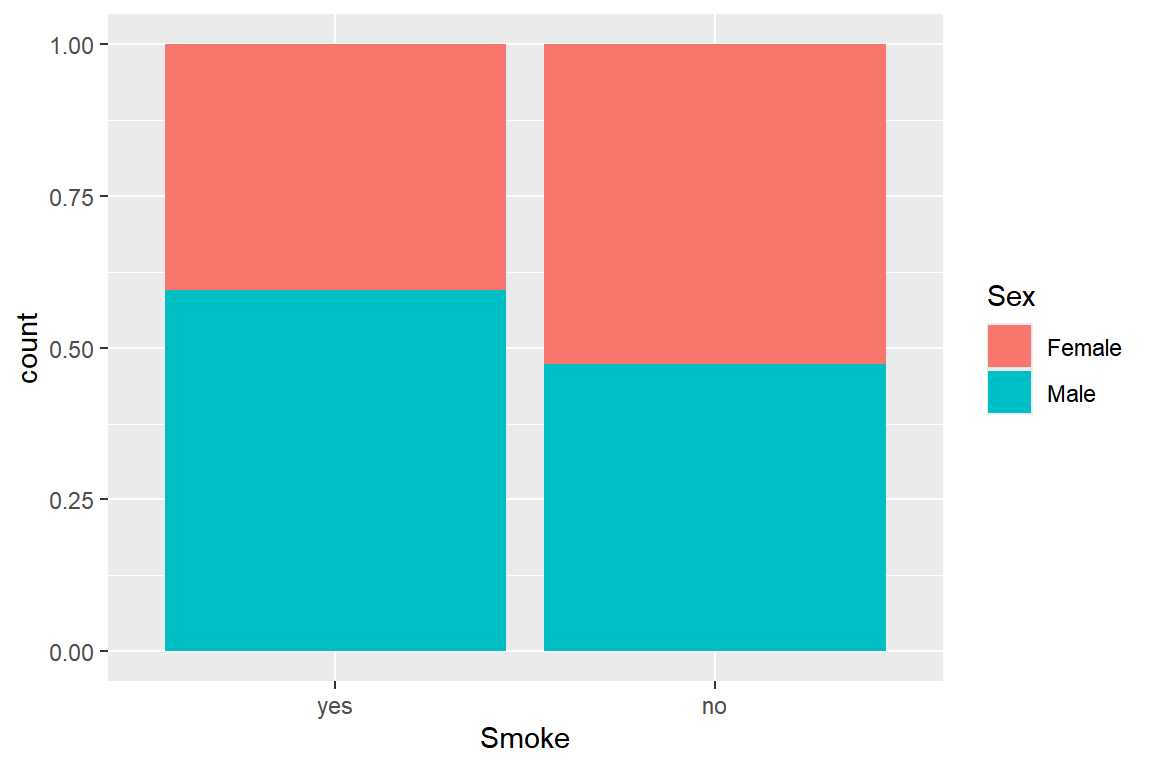
  • 데이터 프레임 survey_S를 사용해서 변수 Smoke와 Pulse의 관계를 살펴볼 수 있는 그래프를 작성하고, 의미를 해석해 보자.

  • 데이터 프레임 survey 중 숫자형 변수의 평균과 표준편차를 계산해서 다음의 형태로 출력해 보자.

## # A tibble: 5 × 3
##   Variable  Mean    SD
##   <chr>    <dbl> <dbl>
## 1 Wr.Hnd    18.7  1.88
## 2 NW.Hnd    18.6  1.97
## 3 Pulse     74.2 11.7 
## 4 Height   172.   9.85
## 5 Age       20.4  6.47
  • 데이터 프레임 survey 중 숫자형 변수의 히스토그램과 확률밀도함수 그래프를 다음과 같이 서로 겹치게 보이도록 작성해 보자. 히스토그램의 경우 구간의 개수는 15로 지정한다.

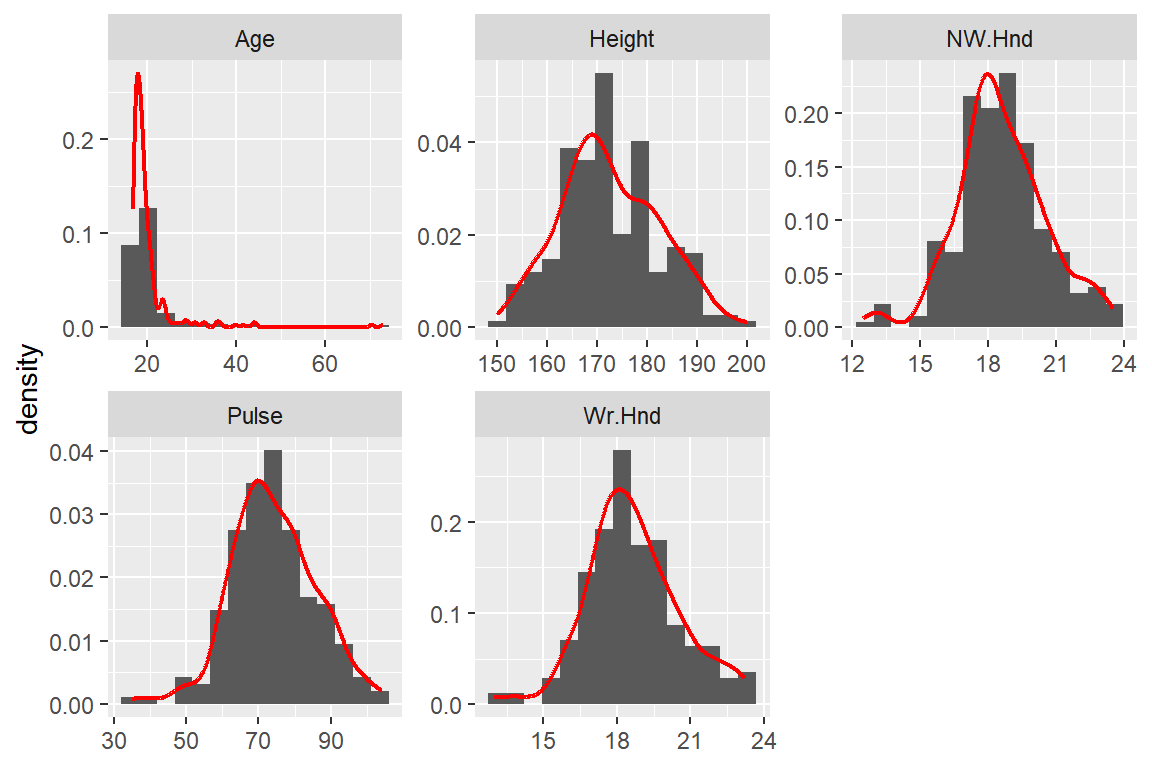
3. 패키지 MASS의 데이터 프레임 Cars93는 1993년 미국에서 판매된 93대 자동차에 대한 자료이다.

  • 변수 Cylinders의 값이 4, 6, 8인 자동차의 Price에 대한 상자그림을 다음과 같이 작성해 보자. 각 상자그림에서 이상값으로 표시된 관찰값 중 최대값에 대해서는 변수 Make의 값을 라벨로 그래프에 추가했다.

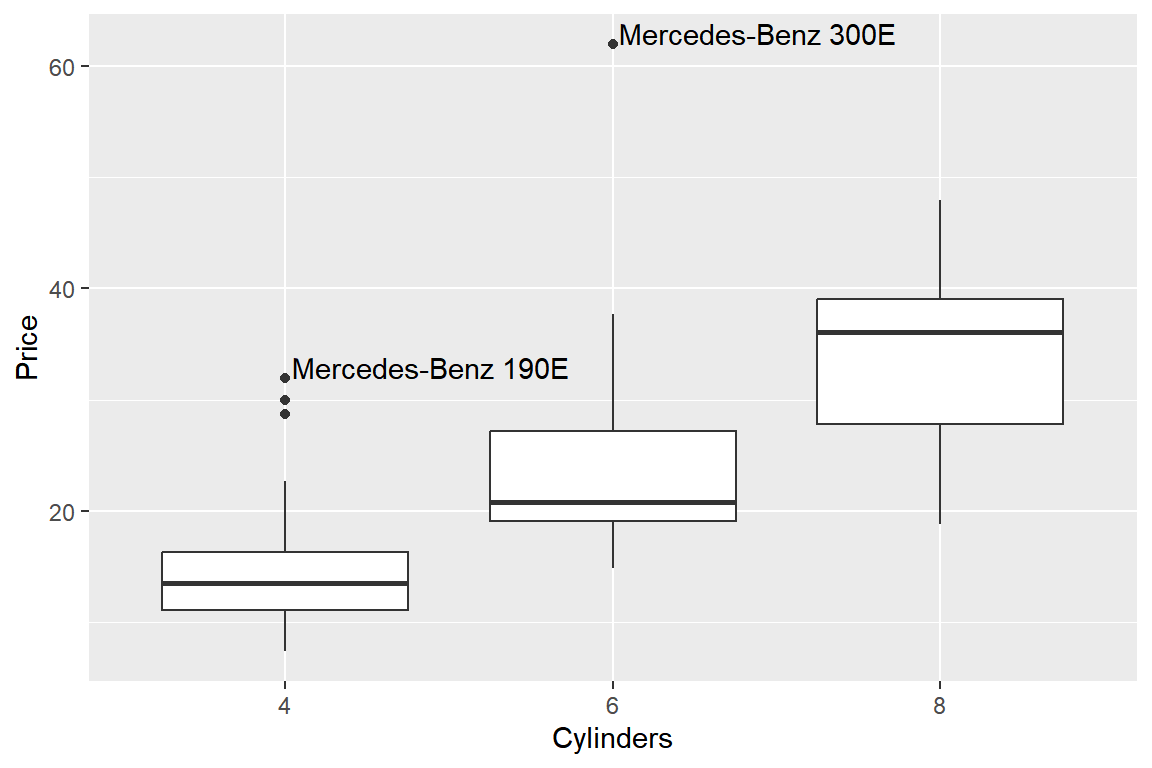
  • 변수 Cylinders의 값이 4, 6, 8인 자동차에 대하여 변수 Price와 Horsepower의 관계를 살펴볼 수 있는 그래프를 작성하고, 그 의미를 해석해 보자.

4. 패키지 ggplot2에 있는 데이터 프레임 diamonds는 53940개 다이아몬드의 가격 및 몇 가지 제원이 입력된 자료이다. 다이어몬드 가격 price와 무게 carat, 그리고 선명도 clarity의 관계를 살펴보고자 한다.

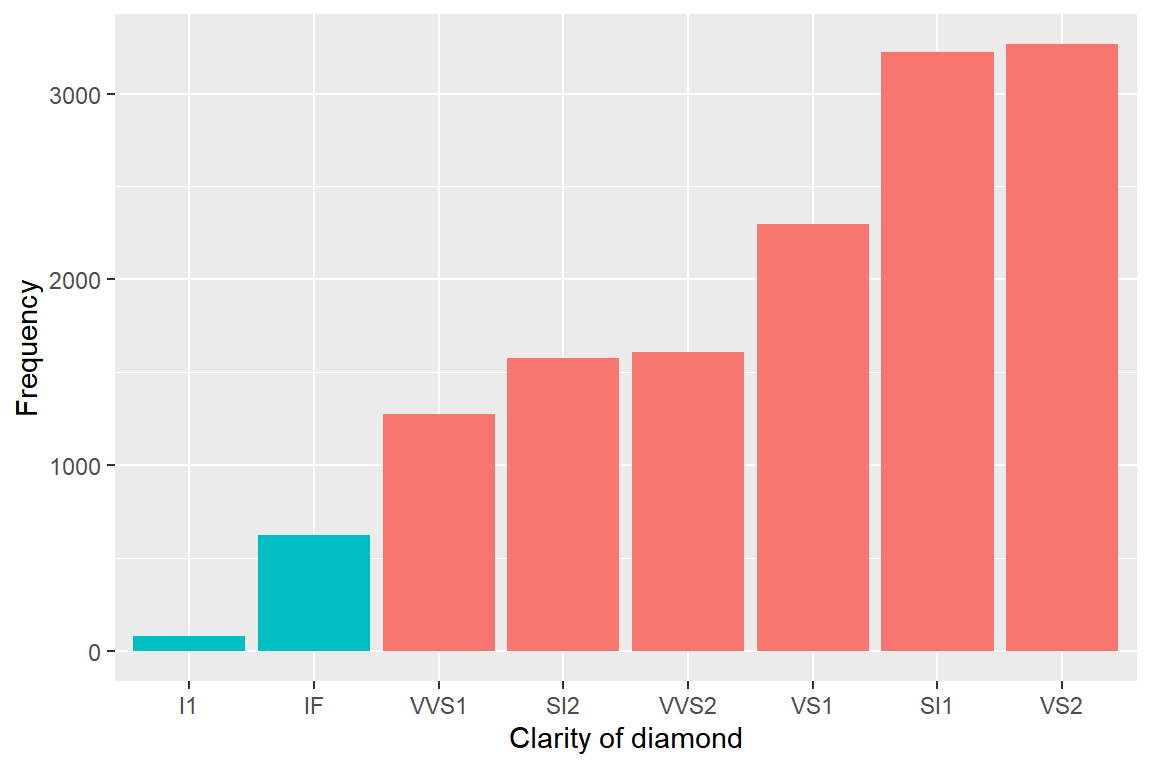
  • 변수 clarity의 범주별 절대도수와 상대도수를 계산해서 분포를 확인해 보자.

  • 자료의 개수가 너무 많아서 전체 자료보다 일부분을 선택해서 분석하는 것이 더 간편할 것으로 보인다. 변수 carat의 값이 1 미만인 자료 중 40% 자료를 임의추출해서 diamonds_small에 할당하라.

  • 데이터 프레임 diamonds_small의 변수 clarity의 막대그래프를 작성해 보자. 각 범주의 순서는 절대도수의 크기에 따라 순서대로 배치하고, 상대도수가 5% 미만인 범주와 5% 이상인 범주에 대한 막대는 색으로 구분해서 다음과 같이 작성해 보자. diamonds_small은 임의추출된 자료이기 때문에 결과에는 약간의 차이가 있을 수 있다.