8 장 확률분포

확률분포와 관련된 이론들은 통계학의 기본이라고 할 수 있다. R에는 확률과 연관된 많은 함수들이 있다. 이러한 함수들을 이용하면 다양한 확률분포들을 대상으로 특정 사건이 발생할 확률을 계산할 수도 있고, 특정 분포의 분위수를 구할 수도 있으며, 특정 모집단에서 난수를 발생시킬 수도 있다.

8.1 R에서의 확률분포 이름

R에는 각각의 확률분포를 지칭하는 이름이 있다. 예를 들어 정규분포는 “norm”이라는 이름으로 불리는데, 이 이름을 근간으로 하여 그 앞자리에 d, p, q, r을 하나씩 붙이는 방식으로 아래와 같이 분포와 관련된 네 종류의 함수가 정의된다.

함수 기능
dnorm 확률밀도함수
pnorm 누적분포함수
qnorm 분위수함수
rnorm 난수발생함수

일반적으로 많이 사용되는 연속형 확률분포와 이산형 확률분포의 R 이름 및 그 이름을 근간으로 정의되는 분포와 관련된 네 종류의 함수에서 중요한 역할을 하는 모수들이 아래의 두 표에 정리되어 있다.

연속형 확률분포의 R 이름
연속형 확률분포 R 이름 관련된 모수
베타분포 beta shape1 , shape2 : 베터분포의 두 모수
코쉬분포 cauchy location : 위치모수, scale : 척도모수
카이제곱분포 chisq df : 자유도
지수분포 exp rate : 비율 (평균의 역수)
F-분포 f df1 df2 : 자유도
감마분포 gamma shape : 형태모수, scale : 척도모수
로지스틱분포 logis location : 위치모수, scale : 척도모수
정규분포 norm mean : 평균, sd : 표준편차
t-분포 t df : 자유도
균등분포 unif min : 하한, max : 상한
와이블분포 weibull shape : 형태모수, scale : 척도모수
이산형 확률분포의 R 이름
이산형 확률분포 R 이름 관련된 모수
이항분포 binorm size : 실행횟수, prob : 성공 확률
기하분포 geom prob : 성공확률
초기하분포 hyper m : 바구니 속 흰 공 개수, n : 바구니 속 검은 공 개수, k : 바구니에서 추출된 공의 개수
음이항분포 nbinom size : 성공 실행 횟수의 목푝값, prob : 성공확률
포아송분포 pois lambda : 평균

위의 두 표에 정리되어 있는 분포들은 모두 R의 base 시스템에 설치되어 있는데, 이외에도 다양한 분야에서 사용되는 많은 분포들이 여러 패키지에 설치되어 있다.

확률분포와 관련된 패키지의 소개는 CRAN Task View: Probability Distributions 을 참고하기 바란다.

8.2 연속형 확률분포

일반적으로 가장 빈번하게 사용되는 정규분포, 지수분포, 균등분포 그리고 t-분포와 관련된 R 함수들의 사용법을 자세하게 살펴보자.

8.2.1 정규분포

정규분포와 관련된 네 종류 함수들의 일반적인 사용법은 다음과 같다.

함수 사용법
확률밀도함수 dnorm(x, mean = 0, sd =1)
누적분포함수 pnorm(q, mean = 0, sd = 1, lower.tail = TRUE)
분위수함수 qnorm(p, mean = 0, sd = 1, lower.tail = TRUE)
난수발생함수 rnorm(n, mean = 0, sd = 1)

단, x는 확률변수가 취하는 값, q는 분위수, p는 확률, n은 표본 크기를 각각 나타낸다.

정규분포와 관련된 함수들에서 공통적으로 사용된 mean과 sd는 모집단의 평균과 표준편차를 나타내는 것으로 각각 0과 1을 디폴트 값으로 하고 있다. 따라서 표준정규분포를 대상으로 하는 경우에는 mean과 sd를 생략할 수 있으나, 일반적인 정규분포를 대상으로 하는 경우에는 반드시 평균과 표준편차를 따로 지정해야 한다.

함수 dnorm()은 정규분포의 확률밀도함수 값을 계산하는 함수이다. 이 함수를 이용하여 정규분포 확률밀도함수의 그래프를 그려 보자. 예를 들어 표준정규분포의 확률밀도함수와 평균이 1, 표준편차가 0.5인 정규분포의 확률밀도함수를 -3에서 3의 구간에서 그려보자.

ggplot2에서 특정 함수의 그래프 작성은 stat_function()으로 할 수 있다. 이 경우 입력되는 데이터 프레임은 X축의 범위를 지정하는 두 숫자로만 구성하면 된다.

library(tidyverse)
ggplot(tibble(x = c(-3, 3)), aes(x)) +
  stat_function(fun = dnorm) +
  labs(title = "Standard Normal Distribution", x = NULL, y = NULL)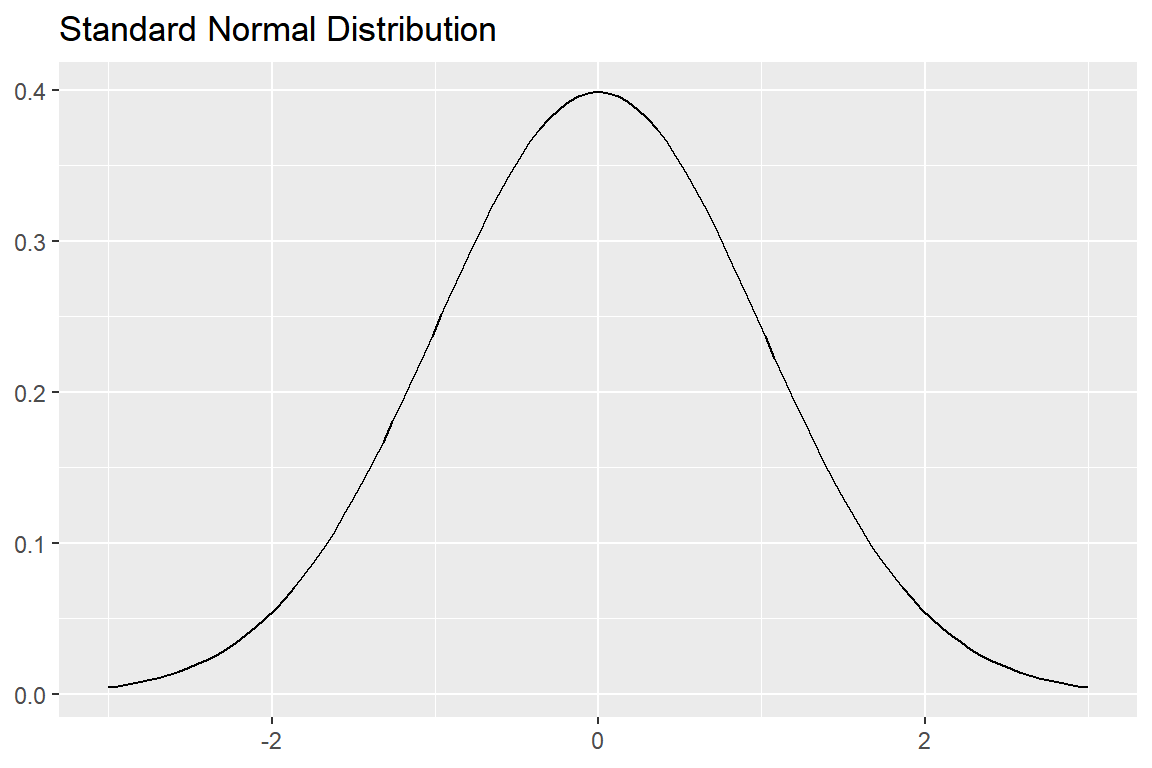
표준정규분포 확률밀도함수 그래프

그림 8.1: 표준정규분포 확률밀도함수 그래프

표준정규분포는 함수 dnorm()의 디폴트 상태이므로 추가로 입력해야 할 것이 없었으나, 평균이 1이고 표준편차가 0.5인 정규분포의 경우에는 dnorm()의 mean과 sd 값을 수정해야 한다. 이러한 경우에는 함수 stat_function()의 변수 args에 수정된 값을 리스트 형태로 입력해야 한다. 또한 제목에 수학 기호 등을 포함시킬 수 있는데, 수학 기호에 대한 R 표현식을 함수 expression()에 입력하여 함수 labs()의 title에 지정하면 된다.

ggplot(tibble(x = c(-3, 3)), aes(x)) +
  stat_function(fun = dnorm, args = list(mean = 1, sd = 0.5)) +
  labs(title = expression(list(mu==1,sigma==0.5)), y = NULL, x = NULL)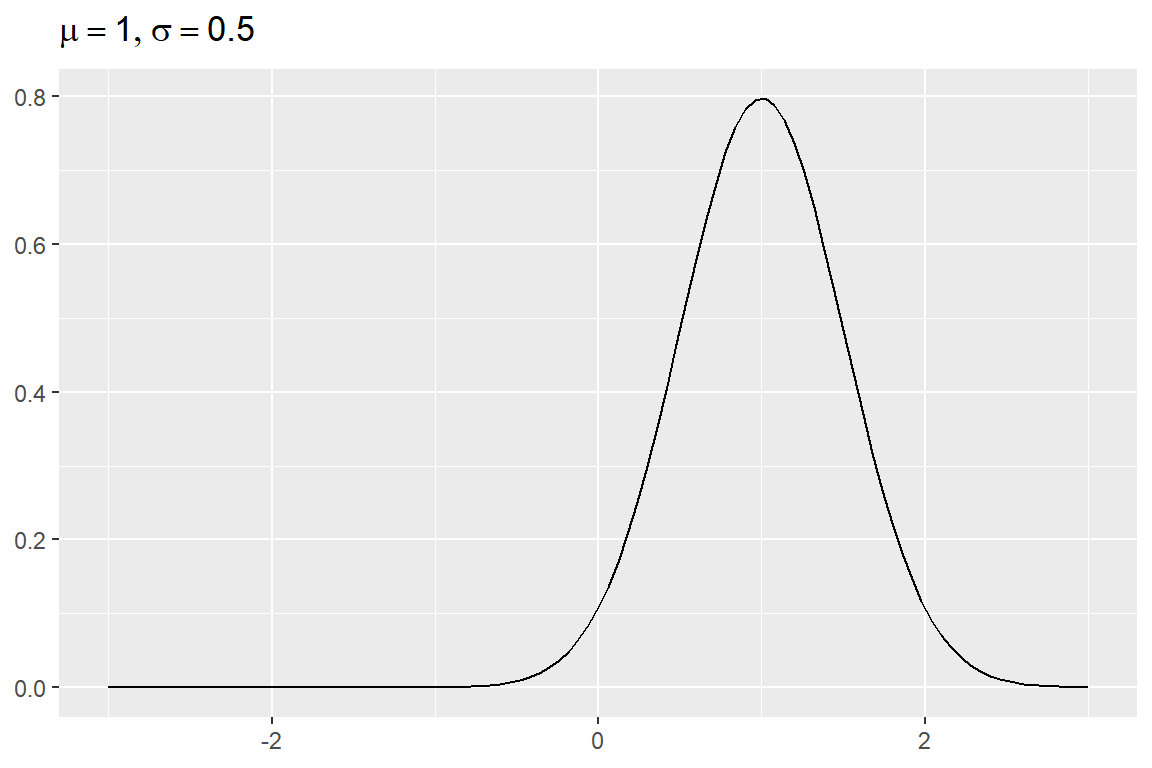
정규분포 확률밀도함수 그래프

그림 8.2: 정규분포 확률밀도함수 그래프

함수 pnorm()은 정규분포의 누적분포함수의 값을 계산하는 함수이다. 따라서 \(X \sim N(m, s^{2})\) 경우 \(P(X \leq q)\) 계산은 pnorm(q, mean = m, sd = s)으로 할 수 있으며, \(P(X > q)\) 값을 계산하고자 한다면 pnorm(q, mean = m, sd = s, lower.tail = FALSE)를 실행시켜야 한다.

pnorm(0)
## [1] 0.5
pnorm(-1.96)
## [1] 0.0249979
pnorm(1.96, lower.tail = FALSE)
## [1] 0.0249979

연속형 확률변수 \(X\) 의 누적분포함수 \(F(x)\) 와 확률밀도함수 \(f(x)\) 의 관계는 다음과 같다.

\[ F(x) = \int_{-\infty}^{x}f(t)dt \]

위 관계를 함수 pnorm()과 dnorm()을 이용하여 확인해 보자. 예를 들어 pnorm(1.645)은 표준정규분포의 확률변수가 1.645 이하의 값을 가질 확률이며, 이 값은 함수 dnorm()을 음의 무한대에서 1.645까지 적분한 결과와 같아야 한다. R에서 1차원 함수의 수치적분은 함수 integrate()로 할 수 있으며 일반적인 사용법은 integrate(FUN, lower, upper)이다. 수치적분의 오차가 무시할만한 수준이며, 계산된 두 확률이 동일함을 알 수 있다.

pnorm(1.645)
## [1] 0.9500151
integrate(dnorm, -Inf, 1.645)
## 0.9500151 with absolute error < 8.7e-08

표준정규분포와 평균이 1, 표준편차가 0.5인 정규분포의 누적분포함수 그래프를 작성해 보자. 함수 stat_function()에 pnorm()을 입력하는 것 외에는 정규분포의 확률밀도함수 그래프 작성과 동일함을 알 수 있다.

ggplot(tibble(x = c(-3, 3)), aes(x)) +
  stat_function(fun = pnorm) +
  labs(title = "Cumulative Standard Normal Distribution", y = NULL, x = NULL)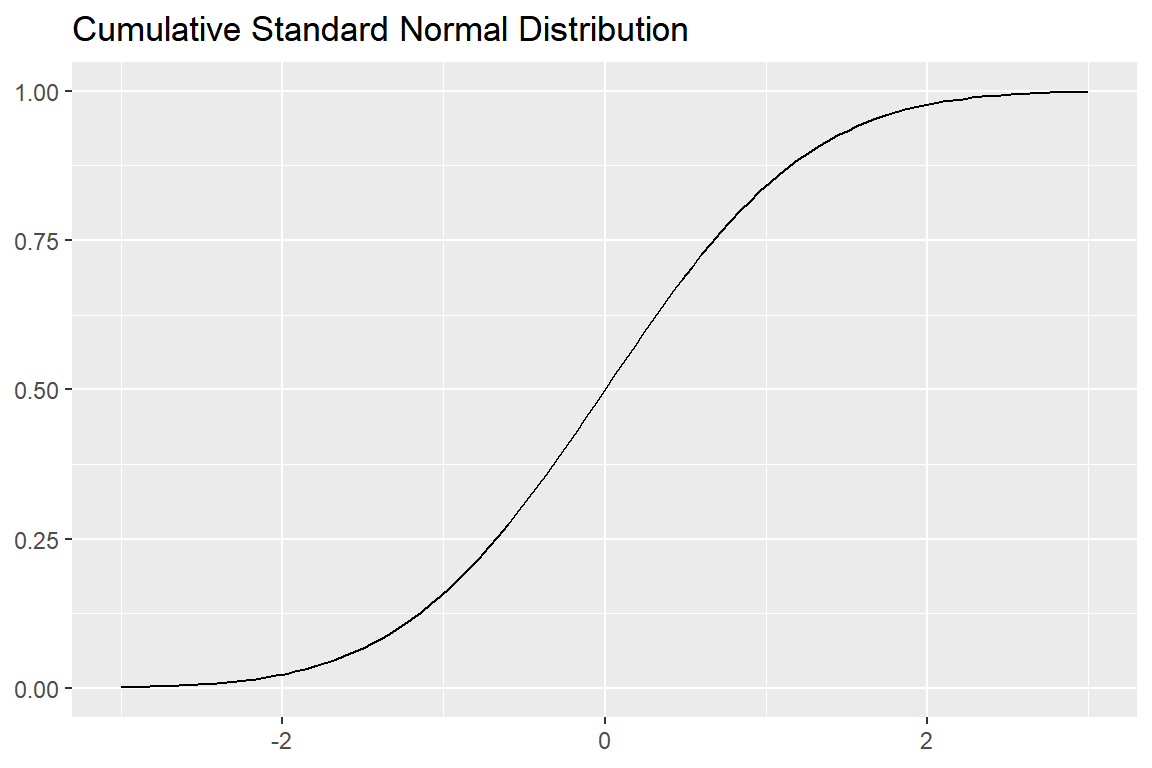
표준정규분포 누적분포함수 그래프

그림 8.3: 표준정규분포 누적분포함수 그래프 

ggplot(tibble(x = c(-3, 3)), aes(x)) +
  stat_function(fun = pnorm, args = list(mean = 1, sd = 0.5)) +
  labs(title = expression(paste("Cumulative Distribution of",~N(1,0.5^2))),
       y = NULL, x = NULL)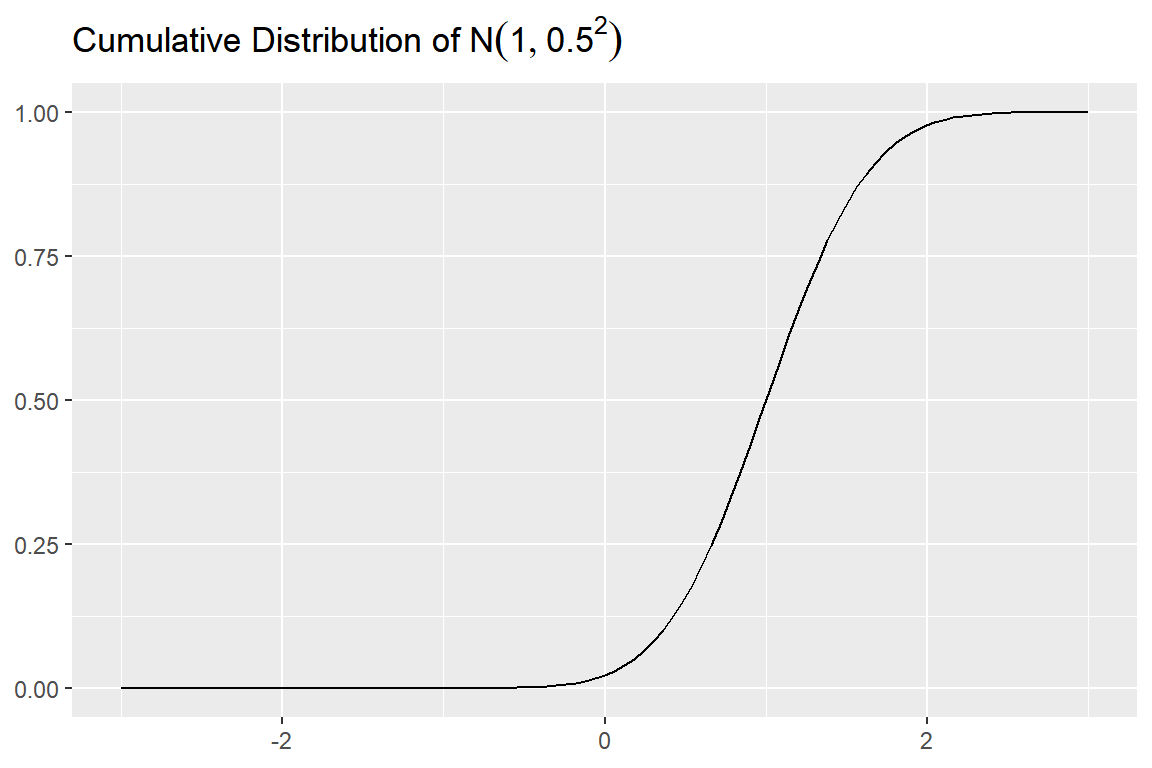
정규분포 누적분포함수 그래프

그림 8.4: 정규분포 누적분포함수 그래프

분위수함수는 누적분포함수의 역함수라고 할 수 있다. 즉, qnorm(p)는 \(p = P(X \leq q)\) 되는 q를 찾아 주며, qnorm(p, lower.tail=FALSE)는 \(p = P(X > q)\) 가 되는 q를 찾아준다.

qnorm(0.5)                     
## [1] 0
qnorm(pnorm(1))               
## [1] 1
c(qnorm(.025), qnorm(.975))    
## [1] -1.959964  1.959964

기초 통계학 수준의 서적에서 흔히 볼 수 있는 표준정규분포의 확률표는 함수 pnorm()과 qnorm()을 적절하게 사용하면 더 이상 참조할 필요가 없을 것이다.

함수 rnorm()은 정규분포에서 난수를 발생시키는 기능을 갖고 있다. 특정 분포에서 난수를 발생시키는 작업은 계산통계분야에서 가장 중요한 기본이 되는데, 검정과 모의실험 등 여러 방면에서 매우 필요한 작업이 된다.

표준정규분포 모집단에서 1000개의 자료를 추출하여 히스토그램을 작성해 보자. 작성된 히스토그램에 표준정규분포의 확률밀도함수 그래프도 덧붙여 그려보자.

히스토그램을 확률밀도함수의 그래프와 덧붙여 그리기 위해서는 히스토그램 막대의 높이를 함수 geom_histogram()에서 계산된 변수 after_stat(density)로 설정해야 한다. 또한 히스토그램의 구간 설정은 구간의 폭을 지정하는 binwidth 또는 구간의 개수를 지정하는 bins으로 할 수 있으며, 디폴트는 bins = 30이다.

set.seed(123)
ggplot(tibble(x = rnorm(1000))) +
  geom_histogram(aes(x = x, y = after_stat(density)), bins = 20) +
  stat_function(fun = dnorm, color = "red", size = 1) +
  labs(x = NULL, y = NULL)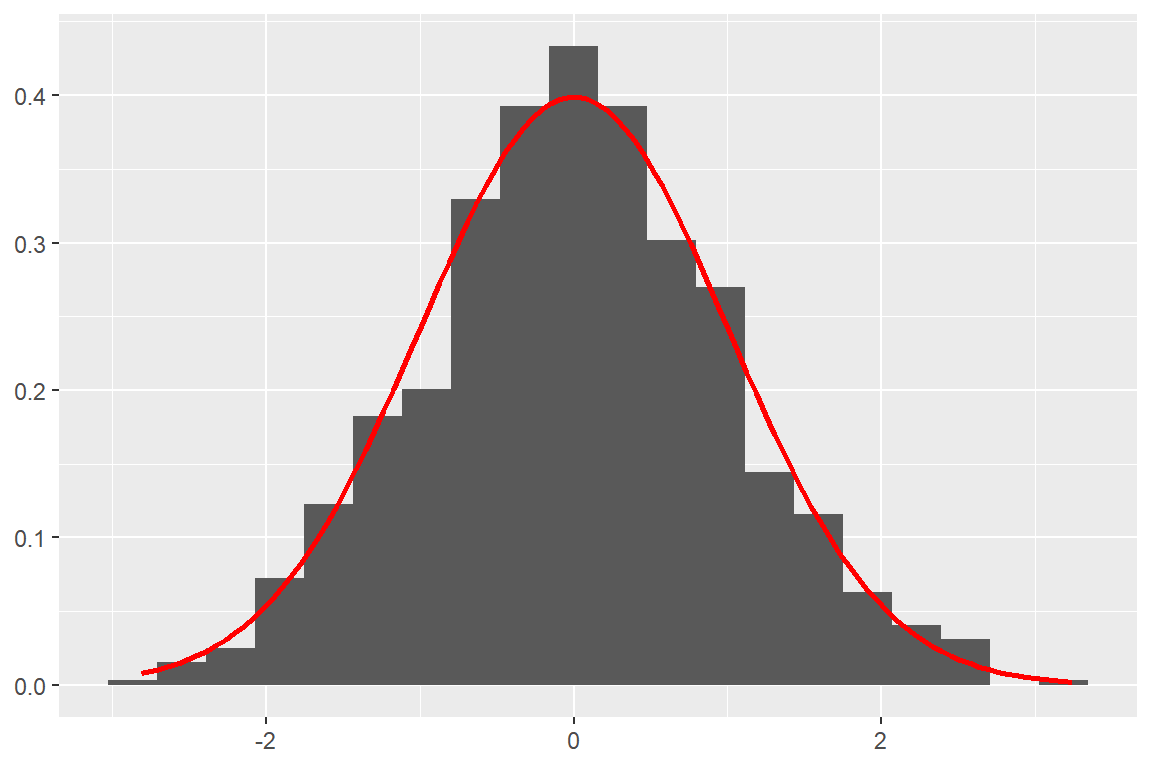
표준정규분포에서 발생된 1000개 난수의 히스토그램

그림 8.5: 표준정규분포에서 발생된 1000개 난수의 히스토그램

8.2.2 지수분포

지수분포는 어떤 특정 사건이 일어날 때까지 걸리는 시간을 나타내는 분포로 빈번하게 사용되고 있다. 예를 들어 어떤 도로의 특정 지점에 다음 차가 지나갈 때까지 걸리는 시간, 전화가 올 때까지 걸리는 시간 등의 분포로 지수분포가 사용된다.

지수분포의 확률밀도함수는 다음과 같다.

\[ f(x)= \lambda~ e^{-\lambda ~x} \] 단, \(x \geq 0\), \(\lambda > 0\) . 평균과 분산은 각각 \(E(X) = 1/\lambda\), \(Var(X) = 1/\lambda^{2}\) 이다.

지수분포와 관련된 R 함수들의 일반적인 사용법은 다음과 같다. 단, 모수 rate는 \(\lambda\) 를 의미한다.

함수 사용법
확률밀도함수 dexp(x, rate = 1)
누적분포함수 pexp(q, rate = 1, lower.tail = TRUE)
분위수함수 qexp(p, rate = 1, lower.tail = TRUE)
난수발생함수 rexp(n, rate = 1)

모수 \(\lambda = 1, 2, 3\) 인 지수분포의 확률밀도함수를 하나의 그래프에 나타내 보자. 함수 stat_function()을 세 번 사용하여, 각 \(\lambda\) 값에 대한 그래프를 작성하면서 시각적 요소 color에 각 곡선의 라벨을 함수 aes() 안에서 매핑함으로써 범례가 추가되도록 하였다.

ggplot(tibble(x = c(0, 4)), aes(x)) +
  stat_function(aes(color = "rate = 1"),
                fun = dexp, size = 1.2) +
  stat_function(aes(color = "rate = 2"),
                fun = dexp, args = list(rate = 2), size = 1.2) +
  stat_function(aes(color = "rate = 3"),
                fun= dexp, args= list(rate = 3), size = 1.2) +
  labs(title = "Exponential \n Distribution", color = NULL, x = NULL, y = NULL)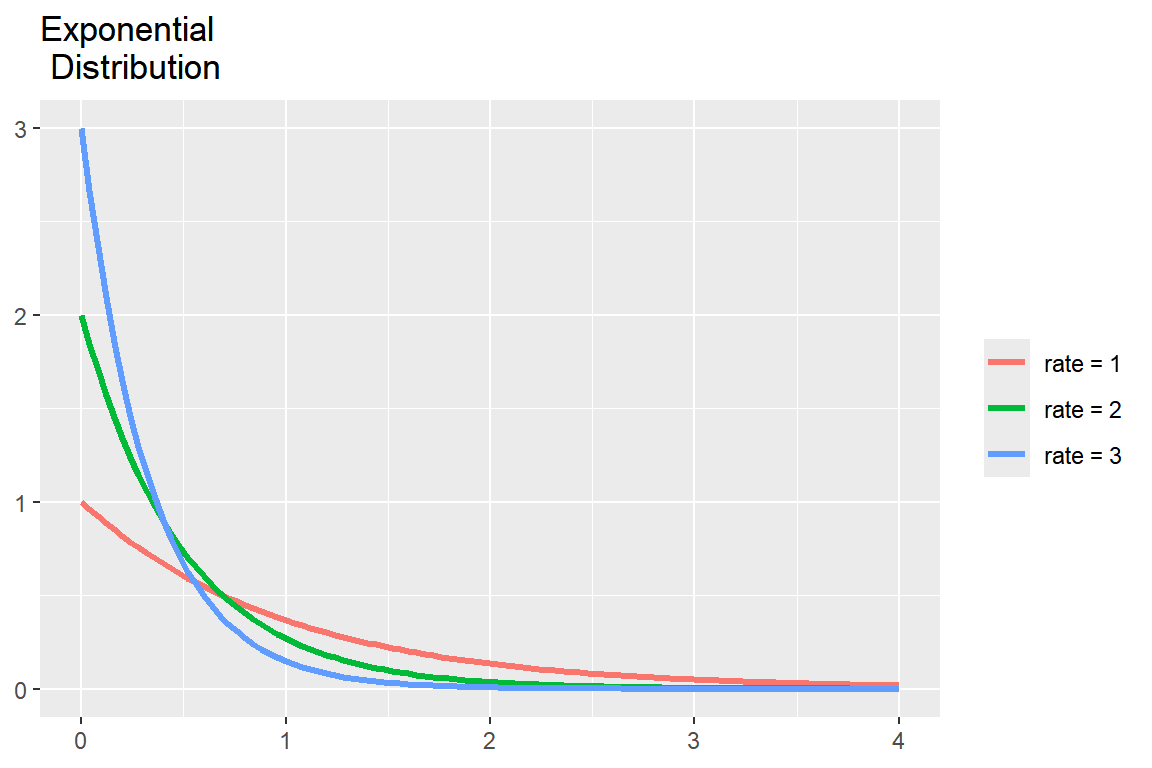
지수분포 확률밀도함수 그래프

그림 8.6: 지수분포 확률밀도함수 그래프

지수분포를 이용해서 해결해야 하는 확률 문제들이 많이 있는데, 함수 pexp()를 이용하면 쉽게 해결할 수 있다. 예를 들어 다음의 문제를 풀어보자.

  • 어떤 은행의 창구대기 시간이 오후 1시쯤에는 평균 5분이 된다고 한다. 오후 1시에 은행에 도착한 사람이 대기 번호표를 뽑고 기다리는 시간이 5분 이상이 될 확률과 5분에서 10분 사이가 될 확률을 구해 보자. 대기시간의 평균이 5분이므로 함수 pexp()에 사용될 모수 rate의 값은 1/5이 되며, 문제의 답은 다음과 같다.
pexp(5, rate = 1/5, lower.tail = FALSE)      # 5분 이상
## [1] 0.3678794
pexp(10, rate = 1/5) - pexp(5, rate = 1/5)   # 5분에서 10분 사이
## [1] 0.2325442

함수 qexp()와 rexp()의 사용법 및 의미 등에 대한 설명은 생략하겠다.

8.2.3 균등분포

구간 \([\alpha, \beta]\) 에서 정의된 균등분포는 그 구간에 걸쳐서 값이 균등하게 퍼져 있는 모집단을 묘사할 때 유용하게 사용되는 분포이다. 확률변수 \(X \sim Unif(\alpha, \beta)\) 의 확률밀도함수는 다음과 같은 상수가 된다.

\[ f(x) = \frac{1}{\beta - \alpha}, ~~\alpha \leq x \leq \beta \]

균등분포와 관련된 R 함수의 일반적인 사용법은 다음과 같다.

함수 사용법
확률밀도함수 dunif(x, min = 0, max = 1)
누적분포함수 punif(q, min = 0, max = 1, lower.tail = TRUE)
분위수함수 qunif(p, min = 0, max = 1, lower.tail = TRUE)
난수발생함수 runif(n, min = 0, max = 1)

균등분포의 확률밀도함수와 누적분포함수의 그래프는 앞 절에서 설명된 방법을 거의 그대로 적용시키면 쉽게 작성할 수 있을 것이며, 균등분포와 관련된 확률 문제도 앞 절에서 설명된 방법을 함수 punif()에 적용하면 어렵지 않게 해결할 수 있을 것이다.

10,000개의 표본을 \(Unif(0, 1)\) 에서 임의로 추출하고, 그 분포를 히스토그램으로 나타내 보자.

set.seed(134)
tibble(x = runif(10000)) %>% 
  ggplot(aes(x, y = after_stat(density))) +
  geom_histogram(bins = 500) +
  labs(x = NULL, y = NULL)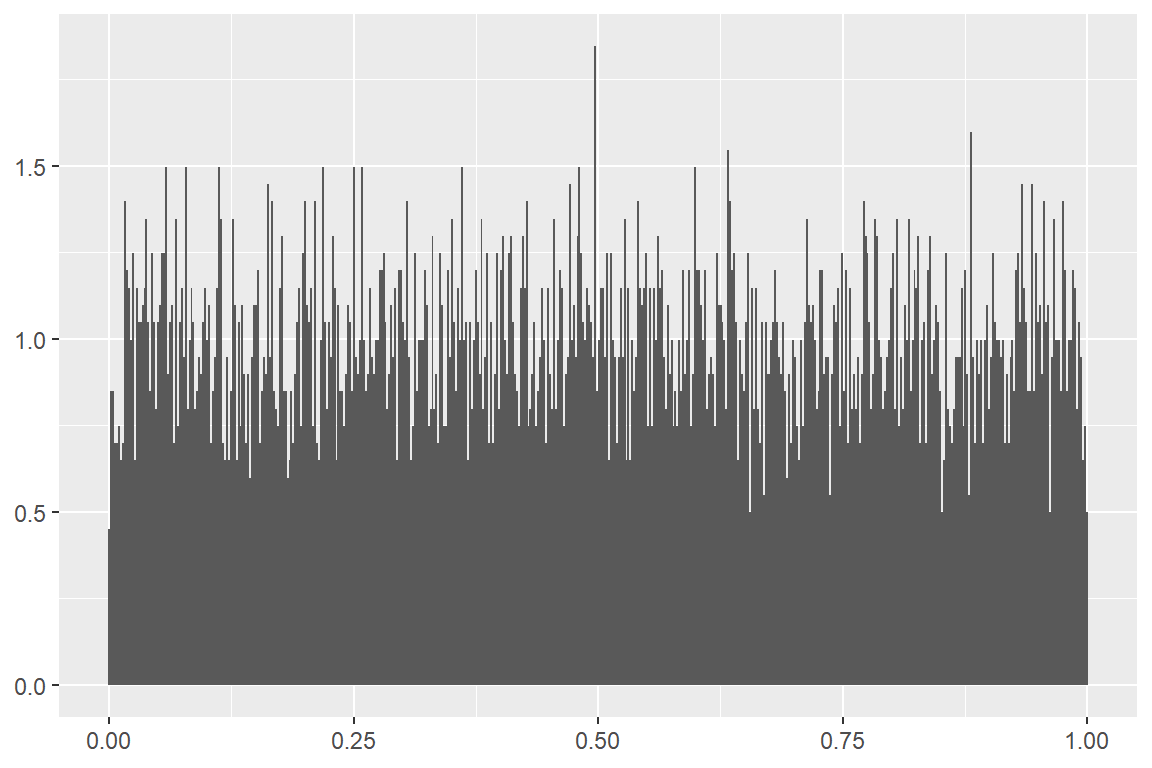
균등분포에서 추출된 표본의 히스토그램

그림 8.7: 균등분포에서 추출된 표본의 히스토그램

8.2.4 t-분포

통계량의 표본분포로 자주 사용되는 분포는 t-분포와 F-분포, 그리고 카이제곱분포이다. 표본크기와 관련된 자유도를 모수로 갖고 있는 분포이며, 각 분포의 R 이름은 각각 t, f, chisq이다. 이들 중 t-분포와 관련된 R 함수들의 일반적인 사용법은 다음과 같다.

함수 사용법
확률밀도함수 dt(x, df)
누적분포함수 pt(q, df, lower.tail = TRUE)
분위수함수 qt(p, df, lower.tail = TRUE)
난수발생함수 rt(n, df)

자유도를 나타내는 df에는 디폴트로 지정된 값이 없음을 알 수 있다. t-분포는 표준정규분포와 동일하게 0을 중심으로 좌우 대칭이지만 분포의 꼬리가 정규분포보다 두껍다는 특징이 있다. 이것을 그래프로 나타내보자.

ggplot(tibble(x = c(-7, 7)), aes(x)) +
  stat_function(aes(color = "N(0,1)"), fun = dnorm, size = 1.2) +
  stat_function(aes(color = "t(1)"), fun = dt, args = list(df = 1), size = 1.2) +
  stat_function(aes(color = "t(2)"), fun = dt, args = list(df = 2), size = 1.2) +
  labs(title = "Normal Distribution \n and t-Distribution", color = NULL, x = NULL, y = NULL)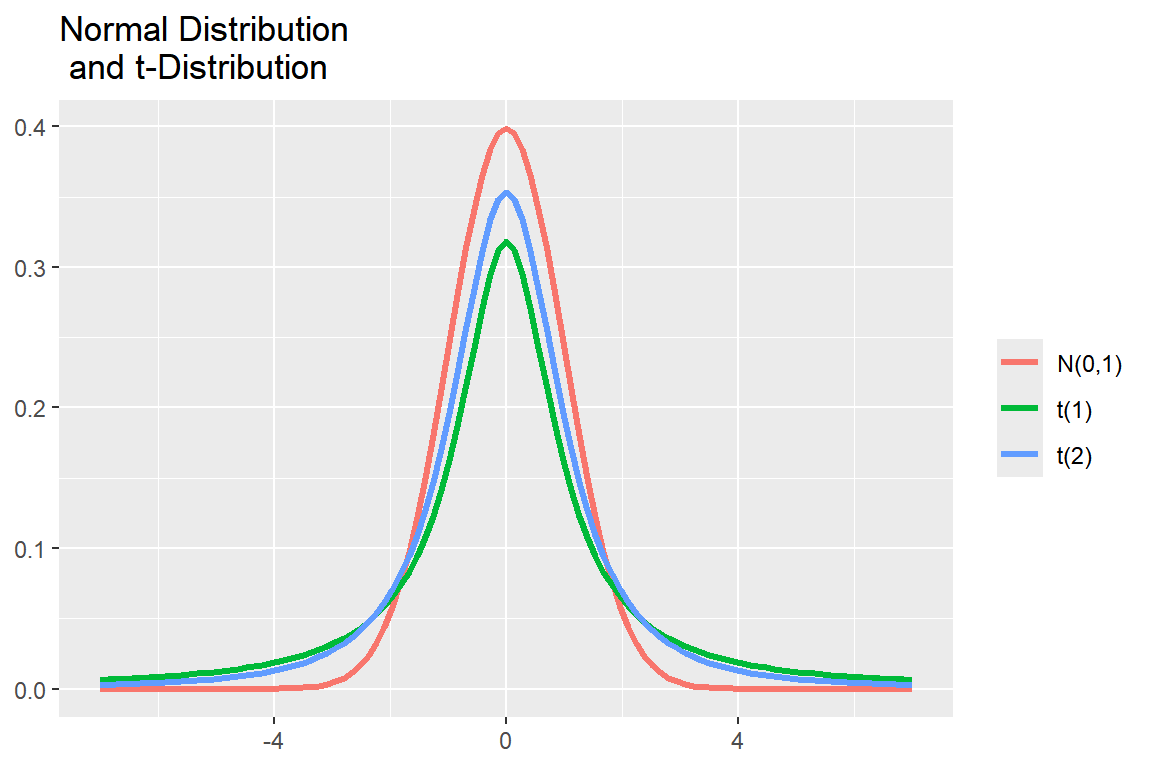
정규분포와 t-분포의 확률밀도함수 그래프

그림 8.8: 정규분포와 t-분포의 확률밀도함수 그래프

8.3 이산형 분포

이산형 확률분포 중 빈번하게 사용되는 분포들과 관련된 R 함수들의 사용법을 살펴보자.

8.3.1 베르누이 분포와 이항분포

확률변수 \(X\) 가 베르누이 분포를 따른다고 하면 \(X\) 가 가질 수 있는 값은 0 혹은 1이 되어야 하며, 분포는 다음과 같아야 한다.

\[ P(X=x)=p^{x}(1-p)^{1-x},~~x=0,1 \]

\(X=1\) 이 되는 사건을 우리는 종종 ‘성공’이라고 부르고, \(X=0\) 이 되는 사건을 ’실패’라고 부른다. 베르누이 시행이란 연속된 통계적 실험으로서, 실험의 결과가 ’성공’ 또는 ‘실패’ 중 하나로 나타나며 ’성공’의 확률은 고정되어 있고 각각의 실험이 서로 독립인 경우를 말한다.

베르누이 시행을 R에서 실시하고자 한다면 함수 sample()을 이용하면 된다. 예를 들어 동전을 10번 던지는 실험에 대응되는 모의실험은 다음과 같다.

set.seed(134)
sample(c("H", "T"), size = 10, replace = TRUE)
##  [1] "T" "T" "T" "H" "T" "T" "T" "H" "T" "H"

위의 예는 \(P(H)=P(T)=0.5\) 가 되는 경우이다. 만일 ’성공’의 확률을 0.2로 하는 베르누이 시행을 실시하고자 한다면 변수 prob를 추가하면 된다.

set.seed(134)
sample(c("H", "T"), size = 10, replace = TRUE, prob = c(0.2, 0.8))
##  [1] "T" "T" "H" "T" "T" "T" "T" "T" "T" "H"

확률변수 \(X\) 가 \(n\) 번의 베르누이 시행에서의 성공 횟수를 나타내는 것이라면 \(X\) 의 분포는 이항분포가 된다. 만일 베르누이 시행의 성공확률이 \(p\) 라고 하면 \(X \sim B(n, p)\) 로 표시하며, 확률분포함수는 다음과 같다.

\[ P(X=x)= \binom{n}{k} p^{x} (1-p)^{n-x}, ~~~x=0,1,\ldots,n \] 이항분포와 관련된 R 함수의 일반적인 사용법은 다음과 같다. 변수 size는 베르누이 시행 횟수를 나타내며 prob는 성공확률을 의미한다.

함수 사용법
확률분포함수 dbinom(x, size, prob)
누적분포함수 pbinom(q, size, prob, lower.tail = TRUE)
분위수함수 qbinom(p, size, prob, lower.tail = TRUE)
난수발생함수 rbinom(n, size, prob)

함수 dbinom()을 사용하여 \(X \sim B(10, 0.5)\) 의 확률분포함수 그래프를 작성해 보자. 입력된 자료 그대로를 사용하여 막대 그래프를 작성하도록 함수 geom_col()을 사용하였고, 막대 폭을 좁게 하여 이산형 확률분포함수를 표현하기 위해 옵션 width = 0.3을 사용하였다. X축의 눈금을 직접 입력하기 위해 함수 scale_x_continuous()에 breaks를 사용하여, 막대마다 해당되는 확률변수의 값을 눈금으로 지정하였다.

tibble(x = 0:10, y = dbinom(x, size = 10, prob = 0.5)) %>%
  ggplot(aes(x, y)) +
  geom_col(width = 0.3) +
  scale_x_continuous(breaks = 0:10) +
  labs(title = "B(10,0.5)", y = NULL, x = NULL)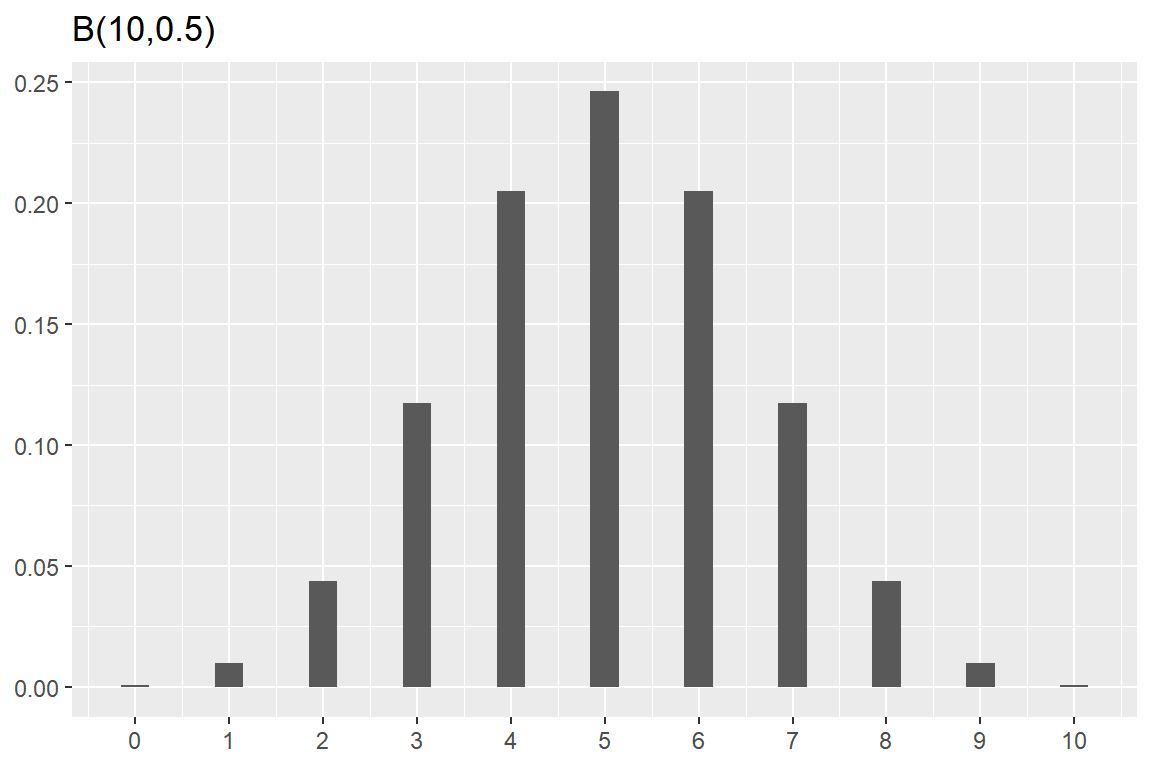
이항분포의 확률분포함수 그래프

그림 8.9: 이항분포의 확률분포함수 그래프

이항분포와 관련된 확률 문제를 함수 dbinom()과 pbinom()을 이용하여 해결해 보자. 예를 들어 \(X \sim B(10, 0.5)\) 의 경우에 다음 사건에 대한 확률을 계산해 보자.

  1. \(P(X=5)\)

  2. \(P(X \leq 6)\)

  3. \(P(X \geq 7)\)

각 사건에 대한 확률을 다음과 같이 구할 수 있다.

# 1)
dbinom(5, size = 10, prob = 1/2)                     
## [1] 0.2460938
# 2)
sum(dbinom(0:6, size = 10, prob = 1/2))              
## [1] 0.828125
pbinom(6, size = 10, prob = 1/2)                     
## [1] 0.828125
# 3)
sum(dbinom(7:10, size = 10, prob = 1/2))             
## [1] 0.171875
1-pbinom(6, size = 10, prob = 1/2)                   
## [1] 0.171875
pbinom(6, size = 10, prob = 1/2, lower.tail = FALSE) 
## [1] 0.171875

함수 pbinom()에 옵션 lower.tail = FALSE가 사용되면 계산되는 확률은 \(P(X>k)\) 이 된다. 따라서 \(P(X \geq 7)\) 을 계산하고자 한다면 함수 pbinom()에 7이 아닌 6을 입력해야 한다.

함수 sample()을 이용하여 R에서 베르누이 시행에 대한 모의실험을 실시하는 방법은 이미 살펴보았다. 함수 rbinom()을 이용해도 동일한 실험을 실시할 수 있다. 1은 성공, 0은 실패를 나타내는 것이고 prob = 0.2는 성공확률, 즉 \(P(x=1)=0.2\) 를 의미하는 것이다.

set.seed(12)
rbinom(10, size = 1, prob = 0.2)
##  [1] 0 1 1 0 0 0 0 0 0 0

\(X \sim B(n, p)\) 의 경우, \(n\) 이 커지게 되면 확률분포함수가 정규분포 \(N(np, np(1-p))\) 로 접근해 간다. 이것을 R에서 나타내 보자. 우선 특정 사건이 발생할 확률을 이항분포에서 구한 값이 \(n\) 이 커짐에 따라 정규분포에서 구한 값에 수렴해 가는 현상을 살펴보자

예를 들어 확률변수 \(X\) 를 주사위를 \(n\) 번 던져 1의 눈이 나온 횟수라고 할 때, 다음의 확률을 이항분포와 정규분포에서 각각 계산해 보자.

  1. 10번 주사위를 던져 1의 눈이 1번 이하로 나올 확률

  2. 100번 던져 1의 눈이 10번 이하로 나올 확률

이산형 분포인 이항분포의 확률을 연속형 분포인 정규분포를 이용해서 계산하는 것이므로 함수 pnorm()에는 수정 계수 0.5를 포함하여 확률을 계산하였다. \(n\) 이 커짐에 따라 이항분포에서 구한 확률과 정규분포에서 구한 확률의 차이가 줄어들고 있음을 알 수 있다.

# 1)
pbinom(1, size = 10, prob = 1/6)                           
## [1] 0.4845167
pnorm(1.5, mean = 10*(1/6), sd = sqrt(10*(1/6)*(5/6)))
## [1] 0.4437685
# 2)
pbinom(10, size = 100, prob = 1/6)                         
## [1] 0.04269568
pnorm(10.5, mean = 100*(1/6), sd = sqrt(100*(1/6)*(5/6)))
## [1] 0.04899367

이번에는 이항분포의 확률분포함수의 형태가 정규분포의 확률밀도함수의 형태로 수렴해 가는 과정을 그래프로 표현해 보자. \(X \sim B(n, p)\) 에서 \(p = 0.2, 0.5, 0.8\) 경우에 \(n = 10,100\) 에 대한 확률분포함수의 그래프를 하나의 그래픽 창에 함께 나타나도록 배치해 보자.

ggplot2에서 여러 개의 그래프를 하나의 그래픽창에 배치하기 위해서는 패키지 patchwork를 사용하면 된다. 그래픽 객체를 먼저 생성하고, 이어서 +와 / 기호를 사용해서 적절하게 배치할 수 있다. 자세한 사용법은 patchwork 에서 찾아볼 수 있다.

n <- c(10, 100)
p <- c(0.2, 0.5, 0.8)
np <- expand_grid(n, p)
p_b <- vector(mode = "list", length = nrow(np))
for(k in 1:nrow(np)){
    df <- tibble(n = np$n[k], p = np$p[k], 
                 x = 0:n, y = dbinom(x, size = n, prob = p))
    p_b[[k]] <- ggplot(df, aes(x, y)) +
      geom_col(width = 0.3) +
      labs(y = "Prob") +
      ggtitle(paste0("X ~ B(", df$n, ",", df$p, ")"))
  }
library(patchwork)
(p_b[[1]] + p_b[[2]] + p_b[[3]])/(p_b[[4]] + p_b[[5]] + p_b[[6]])
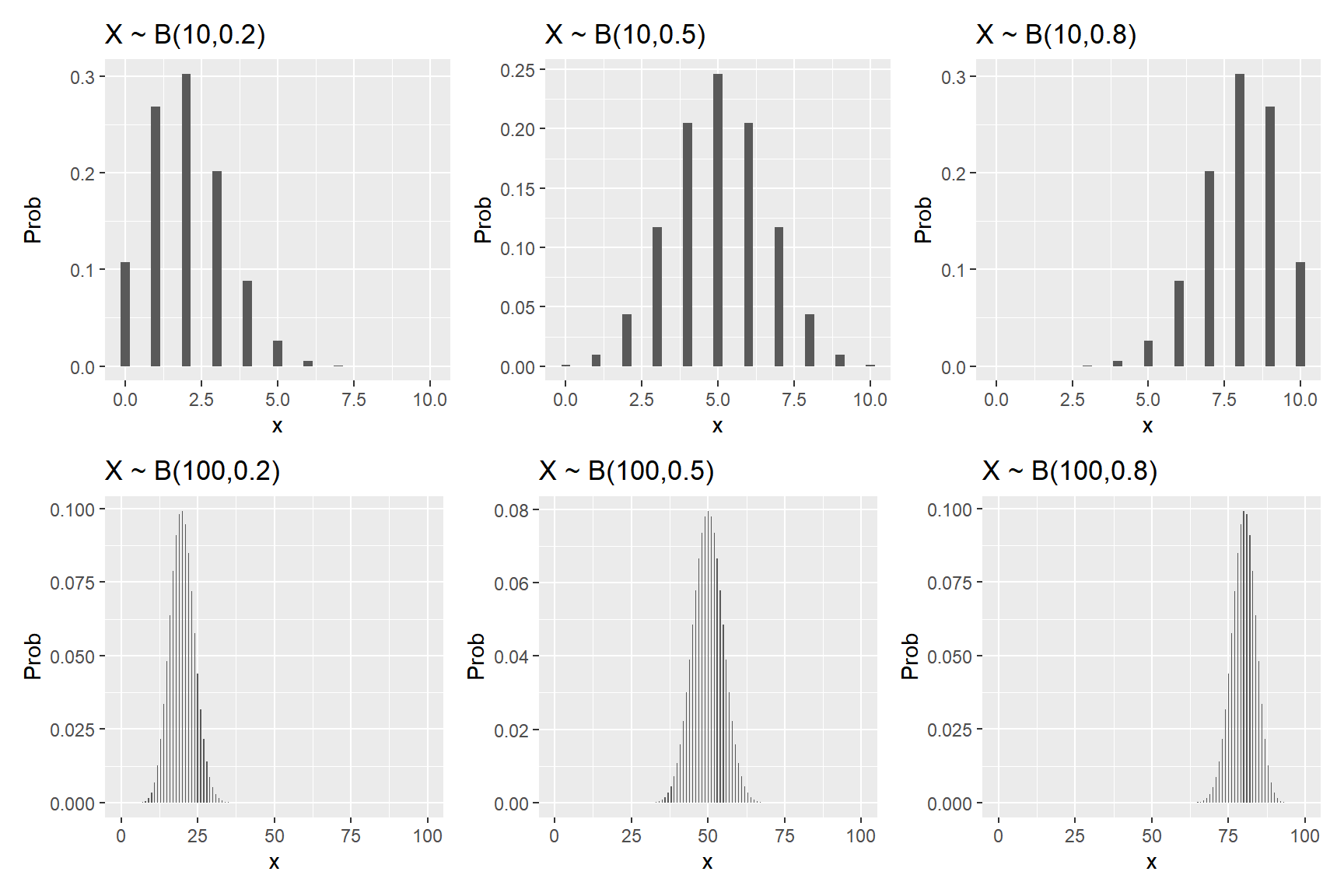
n의 크기에 따른 이항분포 밀도함수 그래프의 변화

그림 8.10: n의 크기에 따른 이항분포 밀도함수 그래프의 변화

\(n\) 이 커짐에 따라 이항분포의 확률분포함수의 형태가 정규분포의 확률밀도함수의 형태와 비슷해짐을 알 수 있다.

8.3.2 포아송 분포

연속형 확률분포인 지수분포는 어떤 특정 사건의 발생 간격에 대한 분포이다. 이에 반하여 포아송 분포는 정해진 기간 내에 어떤 특정 사건이 발생한 횟수에 대한 분포이다. 예를 들어 하루 동안 잘못 걸려온 전화통화 수, 1시간 동안 은행을 방문한 고객의 수, 어느 도로에서 하루 동안 발생한 교통사고 건수, 책 한 페이지당 오타 수 등등이 포아송 분포로 설명될 수 있는 예가 된다.

포아송 분포의 확률분포함수는 다음과 같다.

\[ P(X=x)=e^{- \lambda} \frac{\lambda^{x}}{x!}~, ~~~x=0,1,\ldots \]

포아송 분포와 관련된 R 함수의 일반적인 사용법은 다음과 같다.

함수 사용법
획률분포함수 dpois(x, lambda)
누적분포함수 ppois(q, lambda, lower.tail = TRUE)
분위수함수 qpois(p, lambda, lower.tail = TRUE)
난수발생함수 rpois(n, lambda)

함수 dpois()를 사용하여 \(\lambda=3\) 인 포아송 분포의 확률분포함수 그래프를 작성해 보자.

tibble(x = 0:11, y = dpois(x, lambda = 3)) %>%
  ggplot(aes(x, y)) +
  geom_col(width = 0.3) +
  scale_x_continuous(breaks = 0:11) +
  labs(title = expression(paste("Poisson","(",lambda==3,")")),
       y = NULL, x = NULL)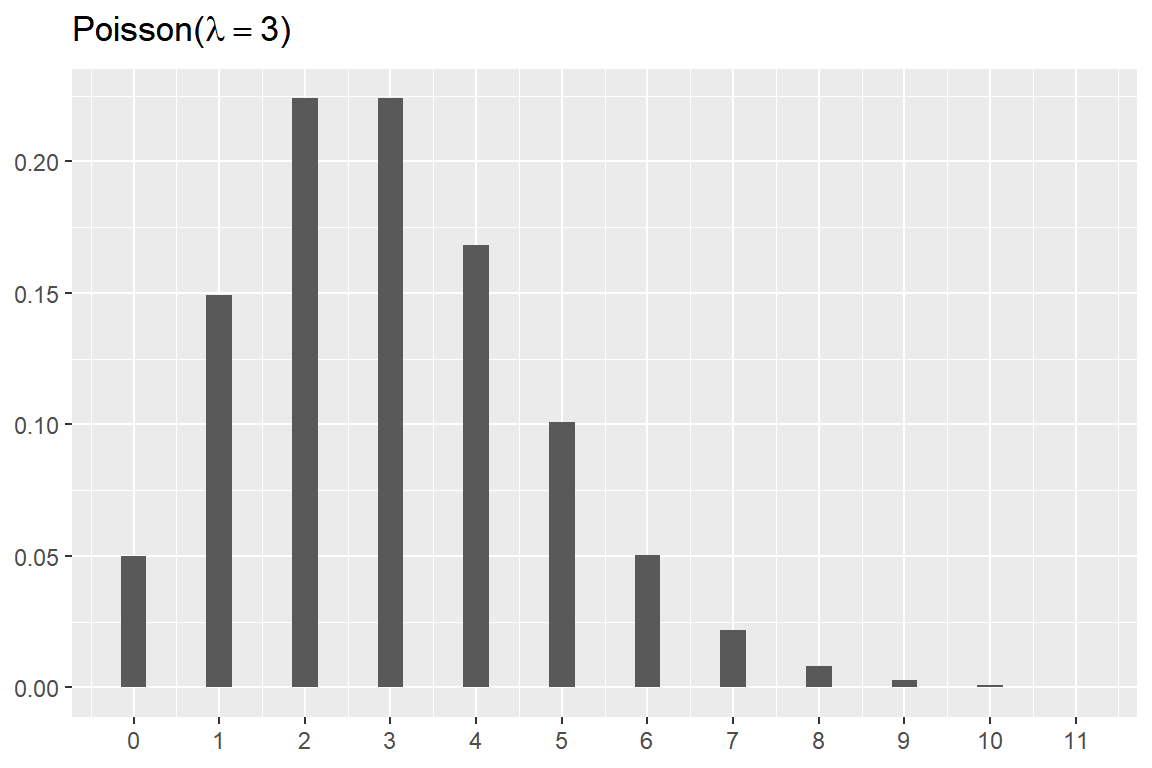
포아송분포의 확률분포함수 그래프

그림 8.11: 포아송분포의 확률분포함수 그래프

포아송 분포와 관련된 확률 문제를 R 함수를 이용하여 풀어보자. 예를 들어 어떤 책의 한 페이지당 오타의 개수가 \(\lambda = 1/2\) 인 포아송 분포를 한다고 했을 때 특정 페이지에서 적어도 한 개의 오타가 나올 확률을 구해 보자. 구하는 확률은 \(P(X \geq 1)\) 이 되는데, 이것은 \(1-P(X=0)\) 과 같기 때문에, 두 가지 방법으로 계산해 보자.

1 - dpois(0, lambda = 1/2)
## [1] 0.3934693
ppois(0, lambda = 1/2, lower.tail = FALSE)
## [1] 0.3934693

포아송 분포가 많이 사용되는 이유 중 하나는 \(n\) 이 크고 \(p\) 가 작은 경우의 이항분포와 매우 비슷한 분포형태가 된다는 것이다. 이 경우 포아송 분포의 모수는 \(\lambda = np\) 가 된다. 이 현상을 R을 이용하여 살펴보도록 하자. 확률변수 X의 분포가 \(X \sim B(n, p)\) 일 때 \(P(X=2)\) 의 값을 \(n=10,~p=0.1\) 인 경우와 \(n=100,~p=0.01\) 인 경우에 이항분포와 포아송 분포를 이용하여 각각 구해 보자.

n <- 10
p <- 0.1
dbinom(2, size = n, prob = p)
## [1] 0.1937102
dpois(2, lambda = n*p)
## [1] 0.1839397
n <- 100
p <- 0.01
dbinom(2, size = n, prob = p)
## [1] 0.1848648
dpois(2, lambda = n*p)
## [1] 0.1839397

포아송 분포의 모수 \(\lambda\) 값은 두 경우 모두 1이 되는데, \(n=100\) 인 두 번째 경우에 포아송분포에서 구한 확률이 이항분포에서 구한 확률에 훨씬 더 근접한 값이 됨을 알 수 있다.

8.3.3 초기하분포

어떤 바구니에 \(m\) 개의 흰 공과 \(n\) 개의 검은 공이 들어있다고 하자. 이 바구니에서 \(k\) 개의 공을 비복원추출 방식으로 임의로 추출했을 때 선택된 흰 공의 개수를 \(X\) 라고 하면, 확률변수 \(X\) 는 초기하분포를 따르게 된다.

초기하분포의 확률밀도함수는 다음과 같다.

\[ P(X=x)=\frac{\binom{m}{x} \binom{n}{k-x}}{\binom{m+n}{k}}~,~~~x=0,1,2,\ldots,k \]

초기하분포와 관련된 R 함수의 일반적인 사용법은 다음과 같다.

함수 사용법
획률분포함수 dhyper(x, m, n, k)
누적분포함수 phyper(q, m, n, k, lower.tail = TRUE)
분위수함수 qhyper(p, m, n, k, lower.tail = TRUE)
난수발생함수 rhyper(n, m, n, k)

초기하분포와 이항분포는 모집단을 구성하고 있는 개체가 두 가지 특성만을 지니고 있다는 점에서 공통점을 갖고 있으나, 표본추출방식에서 초기하분포는 비복원추출에, 이항분포는 복원추출에 각각 해당된다는 점에서 차이가 있다.

그러나 \(m\) 과 \(n\) 의 값이 \(k\) 에 비하여 큰 값인 경우에는 복원과 비복원의 차이가 무시될 수 있는 수준이 되어 두 분포 사이에는 큰 차이가 없게 된다. 이 사실을 R을 이용하여 확인해 보자. 모집단의 구성이 \(m=5\), \(n=10\) 의 경우와 \(n=1000\), \(m=2000\) 의 경우에 \(k=5\) 의 크기로 표본을 추출했을 때 \(P(X=1)\) 의 값을 초기하분포와 이항분포에 각각 구해 보자. 이항분포에서는 두 경우 모두 \(p=m/(m+n)=1/3\) 이 된다.

m <- 5
n <- 10
k <- 5
p <- m/(n+m)
dbinom(1, size = k, prob = p)
## [1] 0.3292181
dhyper(1, m = m, n = n, k = k)
## [1] 0.3496503

\(n=1000\), \(m=2000\) 의 경우 두 분포에서 각각 구한 확률이 거의 동일함을 알 수 있다.

m <- 1000
n <- 2000
k <- 5
p <- m/(n+m)
dbinom(1, size = k, prob = p)
## [1] 0.3292181
dhyper(1,m = m, n = n, k = k)
## [1] 0.3293278

초기하분포는 여러 분야에서 응용되는 분포로서 모집단의 개체 수를 추정할 때도 사용할 수 있는 분포이다. 예를 들어 어떤 호수에 살고 있는 물고기의 개체 수를 추정한다고하자. 이러한 경우 다음의 절차에 따라 물고기의 개체 수를 추정할 수 있다.

  1. 호수에서 \(m\) 마리의 물고기를 잡아 꼬리표를 부착시키고 풀어준다. 그러면 호수에는꼬리표가 부착된 \(m\) 마리의 물고기와 꼬리표가 없는 \(n\) 마리의 물고기가 있게 되어 물고기의 개체 수는 모두 \((m+n)\) 마리가 된다.

  2. 다시 \(k\) 마리의 물고기를 잡아서 그 중 꼬리표가 있는 물고기의 마리 수를 \(x\) 라고 둔다. 이때 가정해야 하는 사항은 호수 전체에 꼬리표가 부착된 물고기의 비율인 \(m/(m+n)\)이 잡힌 \(k\) 마리의 물고기에서도 그대로 유지된다는 것이다.

위 실험에서 두 번째 잡힌 \(k\) 마리의 물고기 중 꼬리표가 있는 물고기의 마리 수를 확률변수 \(X\) 라고 두면 \(X\) 는 초기하분포를 따르게 되는데, 위 실험결과 확률변수 \(X\) 의 값은 \(x\) 가 됐다. 이제 \(P(X=x)\) 의 값을 계산해 보면, \(n\) 이 미지수로 남아있기 때문에 확률 값은 \(n\) 의 함수가 됨을 알 수 있으며, \(P(X=x)\) 를 최대화시키는 \(n\) 의 값을 꼬리표가 없는 물고기 개체 수로 추정하는 것이 현실적인 방안이라고 할 수 있다

이제 \(m=50\), \(k=40\), \(x=3\) 의 경우에 \(n\) 의 값을 추정하여 물고기의 총 개체 수를 추정해 보자. 추정절차는 여러 개의 \(n\) 값을 입력하여 확률을 계산하고 그 중 확률이 최대가 되는 \(n\) 값을 선택하는 방식으로 이루어졌다. 확률이 최대가 되는 \(n\) 값을 찾는 데 사용된 함수 \(which.max()\)는 주어진 숫자형 벡터 최댓값의 인덱스, 즉 최댓값의 위치를 찾는 기능을 갖고 있다.

m <- 50 
k <- 40
x <- 5
n <- 200:700
p.n <- vector("double", length = length(n))
for(i in seq_along(n)){
    p.n[i] <- dhyper(x, m = m, n = n[i], k = k)
}
max.n <- n[which.max(p.n)]
tibble(n, p.n) %>% 
  ggplot(aes(x = n, y = p.n)) +
  geom_line(color = "red", size = 1.2) +
  geom_vline(xintercept = max.n, linetype = 2) +
  labs(title = paste0("Total number of fish is estimated by ", m + max.n,
                   "\n(", m, " tagged and ", max.n, " untagged)"),
       x = "untagged fish", y = "probability")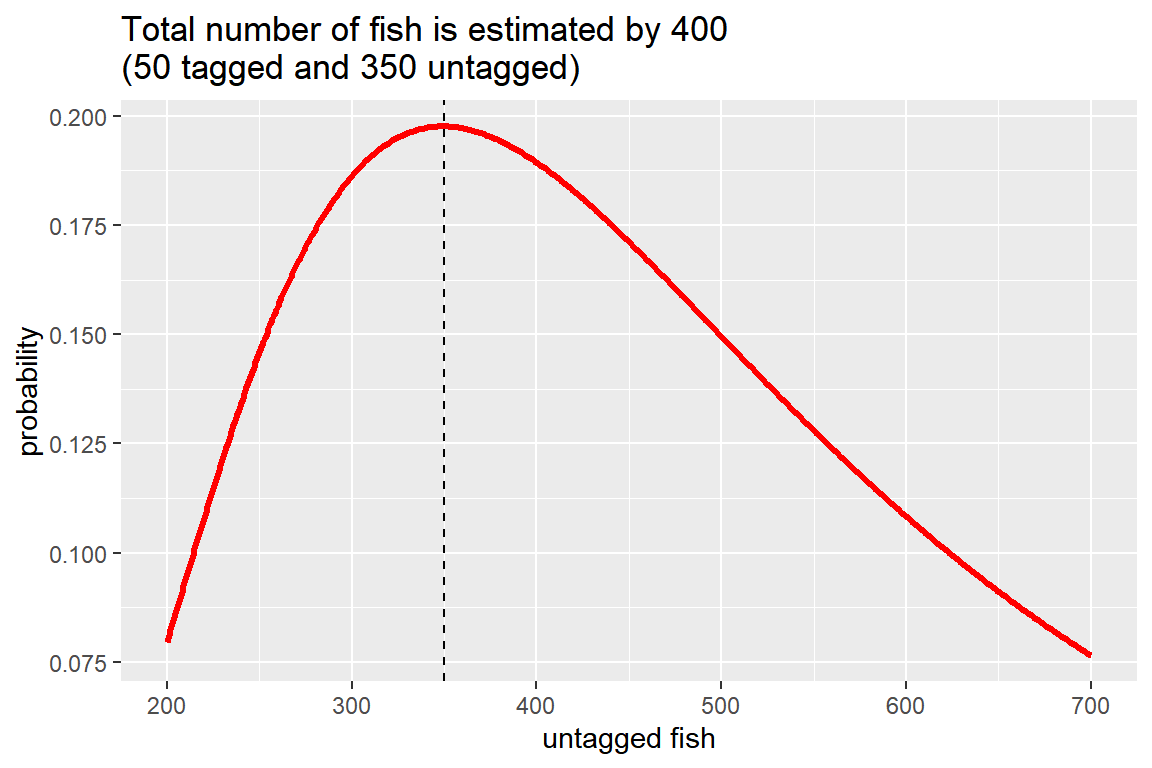
물고기 개체 수 추정 결과

그림 8.12: 물고기 개체 수 추정 결과

여러 개의 \(n\) 값에 대해 계산된 확률값은 geom_line()으로 그렸으며, 최댓값의 위치를 나타내는 수직선은 geom_vline()으로 작성했다. 또한 개체 수 추정 결과가 그래프의 제목에 바로 나타나도록 추정 결과가 할당된 객체를 함수 labs()의 변수 title에 연결하였다.

8.4 모의실험

R에는 매우 효과적인 난수발생함수가 있어서, 다양한 분포에서 손쉽게 난수를 발생시킬 수 있다. 특정 분포에서 난수를 발생시킬 수 있다는 것은 곧 그 특정 분포를 모집단분포로 가정하는 상황에서 표본을 반복해서 추출할 수 있다는 것을 의미하는 것이며, 따라서 어떤 특정 통계적 실험을 반복해서 실행할 수 있다는 것을 의미한다.

이 절에서는 R에 장착된 다양한 분포의 난수발생함수를 이용하여 몇 가지 모의실험 예제를 다뤄보고자 한다. R에서 다루고 있지 않은 분포에서의 난수발생 기법 등을 포함한 모의실험 전체에 대한 체계적인 소개는 Jones and Robinson (2009) 를 참조하기 바란다.

\(\bullet\) 모의실험 예제 1 : 상대도수 개념에 의한 확률

특정 사건 A가 발생할 확률을 상대도수의 개념으로 다음과 같이 정의할 수 있다.

\[ P(A)=\lim_{n \rightarrow \infty} \frac{n(A)}{n} \]

단, \(n\) 은 실험의 시행횟수, \(n(A)\) 는 \(n\) 번의 실험에서 사건 \(A\) 가 발생한 횟수를 각각 의미한다. 이제 상대도수의 개념을 이용하여 주사위를 던져 1의 눈이 나올 확률이 1/6임을 나타내보자. 구체적인 방법은 주사위를 던지는 모의실험을 20,000번 실시하여, 시행마다 1이 눈이 나온 상대도수를 계산하고, 그 변화를 그래프로 나타내는 것이다.

많은 경우 모의실험은 for 루프를 사용하게 되는데, 나름의 장점을 가지고 있는 방법이다. 그러나 경우에 따라서는 for 루프를 사용하지 않고 모의실험을 실시하는 것이 더 효율적일 수 있으므로, 두 방법을 각각 사용하여 모의실험을 실시해 보자.

우선 for 루프를 사용하여 상대도수를 계산해 보자. 주사위를 한 번 던지는 실험은 sample(1:6, 1)로 실시할 수 있고, 그 값이 1과 같게 되면 num의 값을 하나씩 증가시키며, 실행마다 상대도수를 계산하여 객체 prob에 할당하는 방법이다.

set.seed(12)
rep <- 20000
num <- 0
prob <- vector("double", rep)
for(i in seq_along(prob)){
  x <- sample(1:6, 1)
  if(x == 1) num <- num + 1
  prob[i] <- num/i
}

For 루프를 사용하지 않는다면 20,000개의 난수를 한 번에 모두 발생시켜 벡터에 할당하고, 이어서 함수 cumsum()을 사용하여 상대도수를 계산하면 된다. 이 경우에는 더 효율적인 방식으로 보인다.

set.seed(12)
rep <- 20000
x <- sample(1:6, rep, replace = TRUE)
prob <- cumsum(x == 1)/(1:rep)

이어서 계산된 상대도수를 그래프로 나타내 보자. 객체 prob에 저장된 상대도수 값은 함수 geom_line()으로 나타냈고, 확률 1/6을 표시 하는 수평선은 함수 geom_hline()으로 추가하였다. 1의 눈이 나온 상대도수가 1/6로 수렴하는 것을 확인할 수 있다.

tibble(x = 1:rep, y = prob) %>% 
  ggplot(aes(x, y)) +
  geom_line() +
  geom_hline(yintercept = 1/6, color = "red") +
  labs(title = "Relative frequency and Probability",
       x = "Number of Trials", y = "Relative frequency")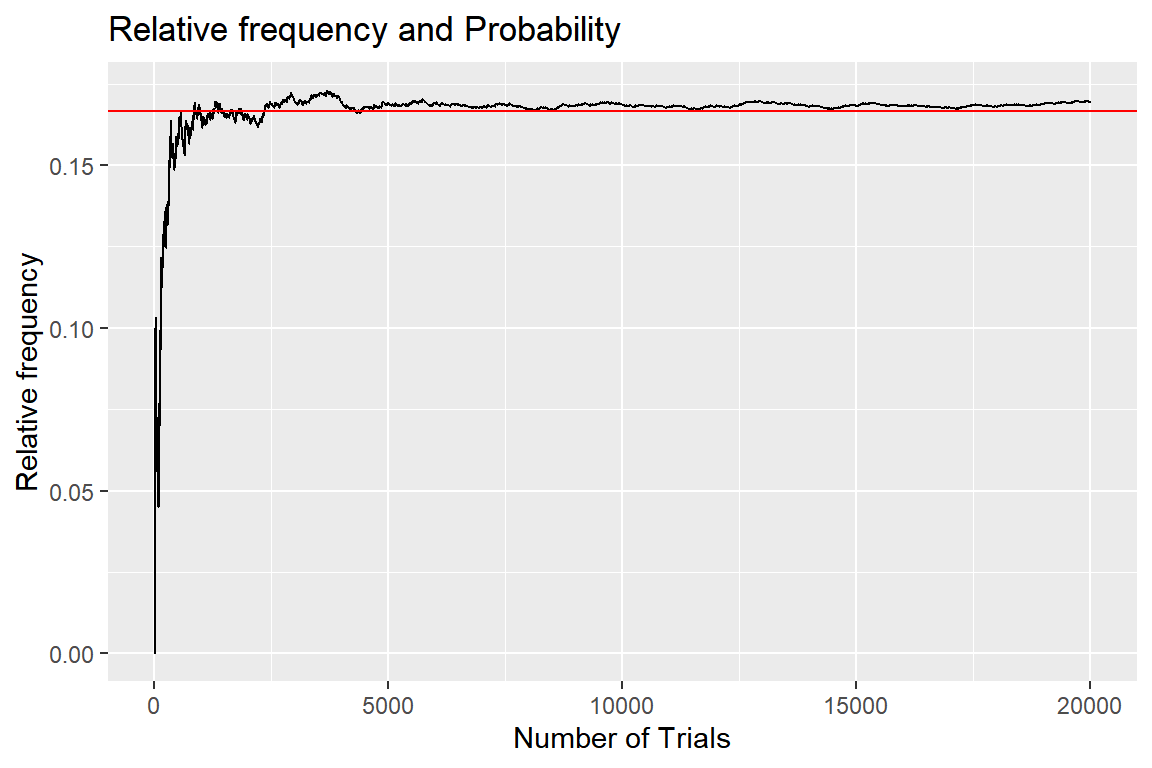
상대도수와 확률

그림 8.13: 상대도수와 확률

\(\bullet\) 모의실험 예제 2 : 표본분포

\(X_{1}, \ldots, X_{n}\) 을 \(N(\mu, \sigma^{2})\) 에서의 확률포본이라고 하자. 그러면 확률변수 \(T=\frac{\bar{X}-\mu}{S/\sqrt{n}}\) 의 분포는 \(t(n-1)\) 을 따르게 된다는 정리를 모의실험을 통하여 확인해 보자.

구체적인 모의실험 절차는 다음과 같다.

  1. \(X_{1}, \ldots, X_{n}\) 을 \(N(\mu, \sigma^{2})\) 에서 추출한다.

  2. 추출된 표본에서 \(T=\frac{\bar{X}-\mu}{S/\sqrt{n}}\) 의 값을 계산한다.

  3. 위 두 단계를 \(N\) 번 반복하여 구한 \(T\) 값의 분포를 \(t(n-1)\) 과 비교한다.

표준정규분포를 대상으로 표본크기를 \(n=5\) 로 하고 반복 횟수를 \(N=10000\) 번으로 하여 \(T\) 통계량 값을 계산하고, 그 결과를 히스토그램으로 작성한 후 \(t(4)\) 의 확률밀도함수 그래프를 겹쳐서 그려보자.

먼저 for 루프를 사용하여 모의실험을 실시해 보자.

set.seed(124)
n <- 5
N <- 10000
Tsample <- vector("double", length = N)
for (i in seq_along(Tsample)) {
    Xsample <- rnorm(n)
    Tsample[i] <- mean(Xsample)/(sd(Xsample)/sqrt(n))
}

For 루프를 사용하지 않는다면 정규분포에서 필요한 난수를 한 번에 모두 발생시키고, 그 결과를 행렬에 할당해야 한다. 이어서 난수 행렬을 대상으로 필요한 통계량을 함수 apply()로 계산하면 된다.

set.seed(124)
n <- 5
N <- 10000
xsample <- rnorm(n*N)
dim(xsample) <- c(n,N)
m.x <- apply(xsample, 2, mean)
sd.x <- apply(xsample, 2, sd)
Tsample <- m.x/(sd.x/sqrt(n))

이어서 객체 Tsample의 값에 대한 히스토그램으로 작성하고, \(t(4)\) 의 확률밀도함수를 겹쳐서 나타내 보자.

tibble(x = Tsample) %>% 
  ggplot() +
  geom_histogram(aes(x = x, y = after_stat(density)), bins = 100) + 
  stat_function(fun = dt, args = list(df = n - 1), color = "red") +
  labs(x = NULL, y = NULL, title = "Sampling Distribution of sample mean")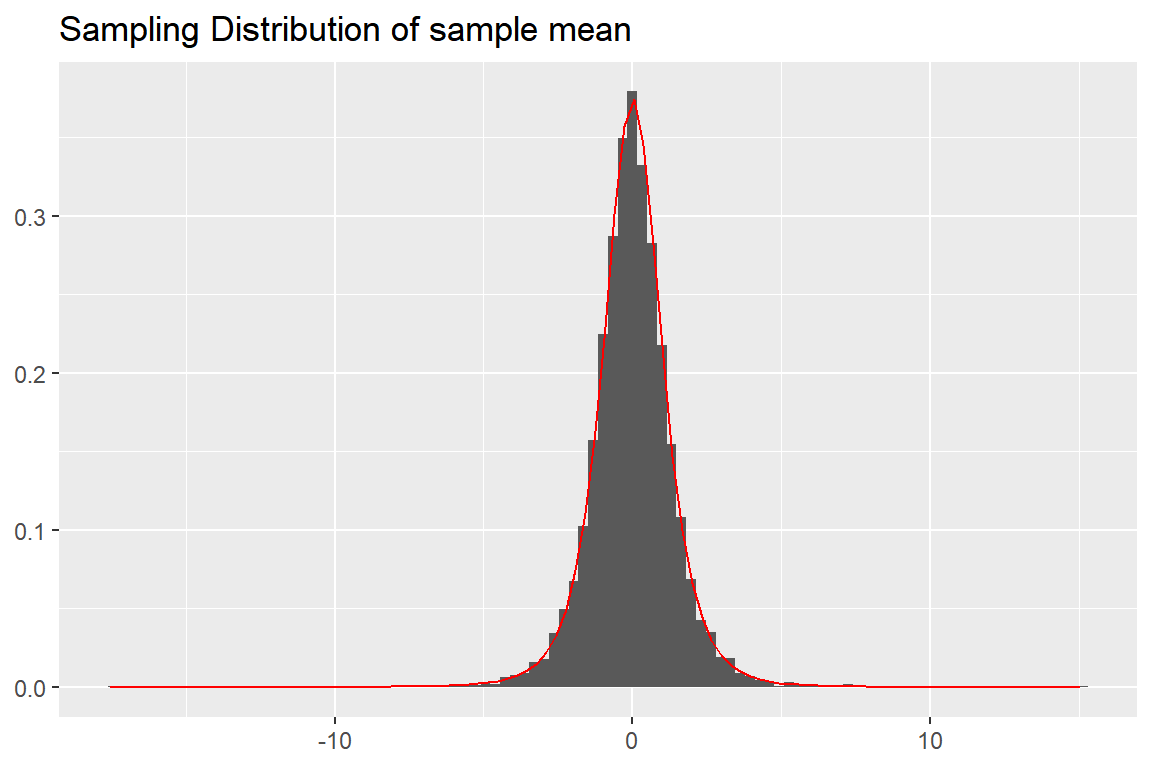
표본평균의 표본분포 그래프

그림 8.14: 표본평균의 표본분포 그래프

\(\bullet\) 모의실험 예제 3 : 신뢰구간에서 신뢰계수의 의미

\(N(\mu, \sigma^{2})\) 의 분포에서 모평균 \(\mu\) 에 대한 95% 신뢰구간은 다음과 같다.

\[ P(\bar{X}-1.96 \frac{S}{\sqrt{n}}\leq\mu\leq \bar{X}+1.96\frac{S}{\sqrt{n}})=0.95 \]

여기에서 신뢰계수 0.95의 의미는 \(n\) 개의 확률표본을 추출하여 신뢰구간을 구하는 작업을 \(N\) 번 반복하여 얻은 \(N\) 개의 신뢰구간 중 95%에는 미지의 모수 \(\mu\) 가 포함되어 있지만, 나머지 5%의 신뢰구간에는 모수 \(\mu\) 가 포함되어 있지 않다는 것이다.

이것을 \(n=20\) 과 \(N=100\) 의 경우에 대한 모의실험을 통해 나타내 보자. 먼저 100개의 신뢰구간을 계산하고, 각 신뢰구간에 모평균 포함 여부를 확인해야 한다.

먼저 for 루프에 의한 방법이다.

set.seed(123)
n <- 20; N <- 100
mu <- 10; sigma <- 1
alpha <- 0.05
upper <- lower <- vector("double", length = N)
ok <- vector("logical", length = N)
for(i in seq_along(upper)) {
  x <- rnorm(n, mean = mu, sd = sigma)
  upper[i] <- mean(x) + qnorm(1 - alpha/2)*sd(x)/sqrt(n)
  lower[i] <- mean(x) - qnorm(1 - alpha/2)*sd(x)/sqrt(n)
  ok[i] <- mu <= upper[i] & mu >= lower[i]
}

for 루프를 사용하지 않는 방법이다.

set.seed(123)
n <- 20; N <- 100
mu <- 10; sigma <- 1
alpha <- 0.05
x <- rnorm(n = n*N, mean = mu, sd = sigma)
dim(x) <- c(n, N)
x_bar <- apply(x, 2, mean)
x_sd <- apply(x, 2, sd)
lower <- x_bar - qnorm(1 - alpha/2)*x_sd/sqrt(n)
upper <-x_bar + qnorm(1 - alpha/2)*x_sd/sqrt(n)
ok <- mu >= lower & mu <= upper

계산된 신뢰구간을 선분으로 표시하기 위해서는 함수 geom_segment()를 사용해야 한다. 이 함수의 필수 매핑 대상으로는 선분의 시작점을 나타내는 시각적 요소 x, y와 끝점을 나타내는 xend, yend가 있다. 신뢰구간 선분을 수직으로 표시할 것이라면, Y축에는 신뢰구간의 상한과 하한을 표시하고 X축은 신뢰구간의 일련번호를 표시해야 할 것이다. 따라서 y에는 객체 lower를 연결하고, yend에는 객체 upper를 연결하며, x와 xend 모두에는 1:N을 동일하게 연결한다. 또한 모평균의 포함 여부를 색으로 표시하기 위해 객체 ok를 color에 매핑하는 것도 필요하다.

tibble(lower, upper, ok) %>% 
  ggplot() +
  geom_segment(aes(y = lower, yend = upper, x = 1:N, xend = 1:N, color = ok),
               size = 1) +
  labs(title = paste("모평균이 포함된 신뢰구간 비율:", mean(ok)),
       color = "모평균 포함", x = NULL, y = NULL) +
  theme(plot.title = element_text(face = "bold", size = 20))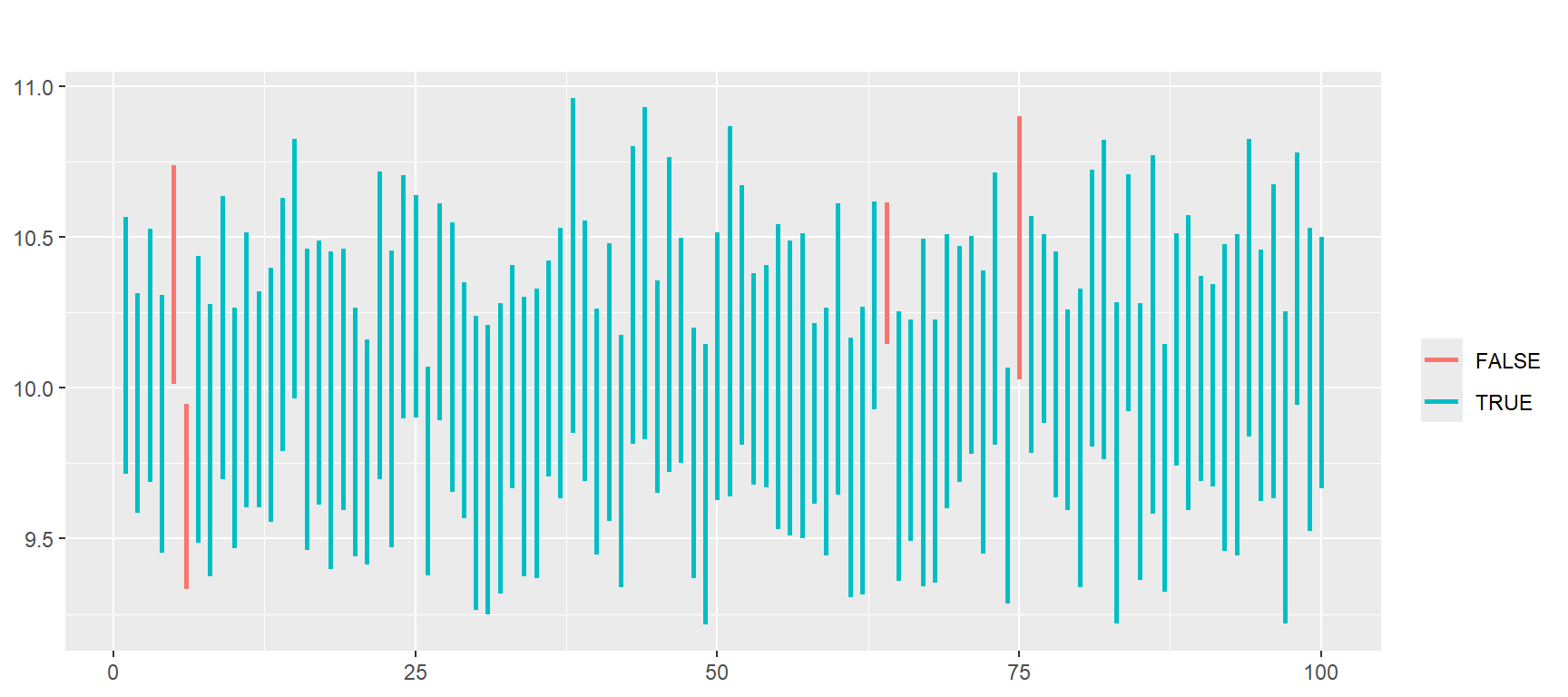
신뢰계수의 의미

그림 8.15: 신뢰계수의 의미